100+ Tổng hợp lời chúc trung thu hay, ý nghĩa nhất
Tết Trung thu hay còn được gọi là Tết đoàn viên là dịp để mọi người trong gia đình cùng sum họp, quây quần bên nhau cùng thưởng thức hương vị của những chiếc bánh thơm ngon dưới ánh trăng sáng ấm áp. Và cũng là dịp để mọi người trao đến nhau những lời yêu thương, những lời chúc ngọt ngào. Dưới đây là tổng hợp những lời chúc trung thu ý nghĩa nhất mà các bạn có thể tham khảo để gửi đến những người mình yêu thương trong ngày lễ đoàn viên này.
Lời chúc Trung thu cho bạn bè
Một số lời chúc trung thu gửi đến cho bạn bè thật ý nghĩa:
1. Chúc bạn và gia đình luôn tràn ngập tiếng cười và niềm hạnh phúc trong ngày Tết Đoàn Viên này nhé!
2. Chúc bạn có một ngày Trung Thu thật vui vẻ và ý nghĩa.
3. Chúc bạn luôn may mắn, nhiều vui vẻ và có những phút giây tuyệt vời bên gia đình nhé.
4. Nhân dịp Trung Thu, xin gửi đến bạn và gia đình nhỏ luôn tràn ngập tiếng cười và một ngày Tết Trung Thu đầy niềm vui nhé!
5. Chúc mừng Tết Đoàn Viên, hi vọng vầng trăng ấm áp kia sẽ mang đến hạnh phúc và viên mãn đến cho bạn và gia đình.
6. Chúc bạn có một ngày Trung Thu thật ý nghĩa và trọn vẹn những phút giây tuyệt vời bên gia đình.
7. Chúc cho công việc và cuộc sống của bạn luôn vẹn toàn như vầng trăng rực rỡ ngày Tết Trung Thu.
8. Tôi hy vọng bạn có một mùa Trung Thu vui vẻ và hạnh phúc bên gia đình của mình.

Lời chúc trung thu cho khách hàng
Một số lời chúc trung thu gửi đến khách hàng ý nghĩa:
1. Một mùa Tết Đoàn Viên nữa lại về, là dịp để mọi người quây quần bên nhau, cùng uống trà và thưởng thức hương vị của những chiếc bánh tình thân và nhâm nhi uống trà. Nhân dịp này, công ty xin được gửi đến quý khách hàng những lời chúc tốt đẹp nhất. Hy vọng, sản phẩm của chúng tôi luôn được bạn và gia đình ủng hộ trong khoảng thời gian tới.
2. Tiết trời đang chuyển dần qua mát dịu hơn và thế là một mùa Trung Thu nữa lại về. Nhân dịp này, công ty chúng tôi xin gửi đến quý khách hàng những lời chúc thân thương và ý nghĩa nhất. Chúc cho quý khách hàng luôn có thật nhiều sức khỏe, công việc và cuộc sống viên mãn hạnh phúc.
3. Nhân dịp Tết Trung Thu chúng tôi xin gửi những quý khách hàng và đối tác đã luôn ủng hộ công ty trong chặng hành trình vừa qua. Chúc cho quý khách/quý đối tác có ngày Tết Đoàn Viên trọn vẹn và có những phút giây vui vẻ hạnh phúc bên gia đình. Chúc tôi sẽ ngày càng cố gắng để phát triển hơn trong tương lai.
4. Nhân dịp Tết Trung thu, kính chúc quý khách luôn có nhiều may mắn, vui vẻ và hạnh phúc. Chân thành cảm ơn sự tin tưởng và ủng hộ của quý khách trong thời gian qua. Chúng tôi sẽ không ngừng nỗ lực để ngày càng phát triển hơn trong tương lai.
5. Chúc quý khách hàng – những người đã tin tưởng, ủng hộ và đồng hành cùng chúng tôi trong thời gian vừa qua những lời chúc tốt đẹp và lời cảm ơn chân thành nhất.

Lời chúc trung thu ngắn gọn
Một số lời chúc trung thu ngắn gọn ý nghĩa:
1. Chúc cho em một mùa trung thu nhiều vui vẻ, những ngày tháng tám luôn tràn ngập yêu thương.
2. Chúc bạn ngày tết đoàn viên vui vẻ và hạnh phúc.
3. Chúc em luôn vui vẻ, một đời an nhiên, vinh hoa phú quý.
4. Mong cho cuộc sống và công việc của bạn sẽ luôn vẹn toàn như vầng trăng tròn ngày Tết thung thu.
5. Chúc em lúc nào cũng tiền tài đầy túi, may mắn an vui.

Lời chúc trung thu cho nhân viên
Một số lời chúc trung thu cho nhân viên:
1. Chúc mọi người có mùa Trung thu thật ý nghĩa, vui vẻ bên bạn bè, người thân và gia đình nhé!
2. Chúc bạn sẽ đón một cái Tết đoàn viên vui vẻ bên gia đình và những đứa con của mình.
3. Chúc bạn trung thu năm năm nay và nhiều năm sau nữa sẽ luôn vui vẻ yêu đời.
4. Mong rằng bạn sẽ có một cái Tết Đoàn Viên hạnh phúc viên mãn bên gia đình.
4. Chúc cho đại gia đình bạn Trung thu luôn ngập tràn tiếng cười và an vui.
5. Chúc bạn và gia đình đón trung thu thật vui vẻ nhé.

Lời chúc trung thu cho đối tác
Một số lời chúc trung thu dành cho đối tác
1. Để tri ân khách hàng đã luôn tin tưởng và ủng hộ sản phẩm bên công ty chúng tôi trong suốt thời gian qua, nhân dịp tết trung thu xin gửi đến quý đối tác những lời chúc và món quà ý nghĩa tốt cho sức khỏe gia đình.
2. Công ty chúng tôi xin gửi đến quý đối tác những lời chúc may mắn và ý nghĩa nhân ngày tết đoàn viên sắp tới, chúc đối tác luôn thật nhiều sức khỏe, công việc hanh thông, thuận lời và luôn tràn ngập niềm vui.
3. Kính chúc Quý đối tác một mùa Trung thu vui vẻ và hạnh phúc bên gia đình.
4. Nhân dịp Tết Trung thu, công ty xin gửi lời tri ân tới tất cả Quý đối tác đã, đang và sẽ đồng hành cùng công ty luôn tràn đầy niềm vui, thật nhiều sức khỏe, thành công trong công việc và có mùa Trung thu thật ấm áp, ngọt ngào bên gia đình.

Lời chúc trung thu cho các bé
Một số lời chúc trung thu hay dành cho các bé
1. Chúc các bạn nhỏ nhân dịp trung thu sẽ luôn mỉm cười, ước mơ sớm thành hiện thực và trở thành mầm non tương lai của đất nước.
2. Một mùa Trung thu nữa lại đến rồi, chúc các bé mau ăn chóng lớn, luôn ngoan ngoãn và học thật giỏi nhé!
3. Nhân dịp Trung thu gửi lời chúc đến các bạn nhỏ từ bé trai đến bé gái thật nhiều vui vẻ, ấm áp bên gia đình và nhận được thật nhiều những lời chúc ý nghĩa từ mọi người.
4. Nhân dịp Tết Trung thu ba mẹ chúc những đứa con yêu quý của ba mẹ luôn vui vẻ, thật nhiều sức khỏe, học thật giỏi và trở thành một người tốt nhé.
5. Cuộc sống đôi khi khó khăn và nhiều mệt mỏi buồn phiền nhưng mẹ đã có một điểm tựa ở bên đó là con, chúc con có một tết trung thật vui vẻ và bình an.
6. Nhân ngày Tết Trung thu ba chúc con gái của ba mau ăn chóng lớn và luôn vui vẻ nhé!

Lời chúc trung thu cho doanh nghiệp
Một số lời chúc trung thu cho doanh nghiệp
1. Doanh nghiệp chúng tôi xin gửi đến quý đối tác những lời chúc ý nghĩa nhất nhân dịp trung thu sắp tới. Chúc cho đối tác luôn có thật nhiều sức khỏe, công việc thuận lợi và phát triển để cuộc sống luôn tràn ngập niềm vui.
2. Xin gửi lời chúc đến quý khách hàng đã luôn đồng hành cùng doanh nghiệp chúng tôi trong thời gian qua có một mùa trung thu thật ý nghĩa, vui vẻ và nhiều niềm vui bên gia đình.
3. Nhân dịp tết Trung thu 2022, doanh nghiệp chúng tôi xin gửi đến quý khách hàng và đối tác những lời chúc sức khỏe, thành công trong công việc và thật nhiều may mắn. Nhân đây, chúng tôi cũng muốn gửi những món quà ý nghĩa đến quý bạn đã đồng hành cùng công ty trên con đường phát triển!

Lời chúc trung thu hài hước
Một số lời chúc trung thu hài hước
1. Tổng đài Mobiphone xin thông báo: Thuê bao 09xxx vừa nhận được lời chúc mừng trung thu nhiều vui vẻ, may mắn và kèm theo một chiếc ôm ấm áp từ chủ thuê bao 07xxx.
2. Trung thu lại đến rồi này, tạm gác lại chuyện cơm áo gạo tiền đi nào. Vui vẻ tận hưởng trung thôi thu sắp già hết phần thiên hạ rồi. Trung thu vui vẻ nhé, nhậu không ???
3. Nhân dịp trung thu, mình xin tặng bạn một món quà vô cùng ý nghĩa… đó chính là mình này. Hãy nhận đi và không được từ chối nhận quà đâu đấy!
4. Lâu lắm rồi mình với bạn chưa gặp lại nhau nhưng mình vẫn chúc bạn có một ngày trung thu thật vui vẻ bên mọi người và đừng quên thằng bạn già xác xơ này nhé.

Lời chúc trung thu tiếng anh
Một số lời chúc trung thu bằng tiếng anh hay
1. Happy Mid-Autumn Festiva ! (Chúc mừng tết trung thu)
2. Happy Mid-Autumn Festival! May the round moon bring you a happy family and a successful future. (Chúc mừng ngày tết trung thu! Ánh trăng tròn sẽ mang lại cho bạn một gia đình hạnh phúc và thành công trong tương lai)
3. The roundest moon can be seen in the autumn. It is time for reunions. I wish you a happy Mid-Autumn Day and a wonderful life.
(Vầng trăng tròn nhất sẽ có thể nhìn thấy được vào mùa thu. Đó là dịp đoàn viên. Tôi ước bạn sẽ có một ngày tết trung thu vui vẻ và một cuộc sống tuyệt vời)
4. Wish you a perfect life just like the roundest moon in Mid-Autumn Day. (Hi vọng bạn sẽ có một cuộc sống an nhiên như vầng trăng tròn ngày Tết trung thu).
5. Wishing us a long life to share the graceful moonlight, though thousands of miles apart. (Chúc cho chúng ta sẽ sống thật lâu để sẻ chia ánh trăng đẹp đẽ dù có cách xa nhau hàng ngàn dặm)

Xem thêm:
- TOP 10 bài hát trung thu hay nhất, ưa chuộng mọi thời đại
- Trung Thu ngày mấy? Ý nghĩa, nguồn gốc và phong tục ngày Tết Trung Thu
- 40+ Mẫu trang trí bảng trung thu đẹp, độc lạ, đơn giản, ấn tượng
Trên đây là những lời chúc trung thu hay và ý nghĩa mà bạn có thể gửi đến bạn bè, người thân, đồng nghiệp và mọi người để mang lại niềm vui nho nhỏ trong ngày tết đoàn viên. Học nhanh những câu chúc này ngay nào, trung thu sắp đến rồi đấy!
50+ Bức vẽ tranh trung thu đẹp, đơn giản, dễ nhất cho học sinh
Trung thu đến rồi! Các cuộc thi vẽ tranh với mục đích trao cơ hội để các em thiếu nhi trổ tài hội họa đầy sáng tạo của mình cũng được tổ chức lần lượt. Nếu như các bé vẫn còn đang bí ý tưởng và muốn tham khảo một số hình vẽ nổi bật, vậy thì hôm nay chúng ta cùng điểm qua 50+ Bức vẽ tranh trung thu đẹp, đơn giản, dễ nhất cho học sinh nhé!
Vẽ tranh trung thu dễ nhất
Vẽ các em thiếu nhi vui đồ dưới ánh trăng và những ngôi sao lấp lánh, trên tay là những chiếc lồng đèn ngộ nghĩnh luôn là ý tưởng dồi dào để vẽ tranh trung thu trong các cuộc thi.

Tuy nhiên, nếu như vẽ thiếu nhi đã quá nhàm chán, tại sao chúng ta lại không thử vẽ chính bố mẹ và ông bà thân yêu trong mùa lễ hội này nhỉ? Chắc chắn sẽ là một ý tưởng hết sức độc đáo. Hình ảnh ông bà làm bày mâm ngũ quả cùng cha mẹ chuẩn bị những món ăn và chiếc lồng đèn xinh xinh cũng là một ý tưởng đáng để khai thác đấy!

Phố phường trở nên nhộn nhịp hơn bao giờ hết mỗi khi mùa trung thu lại về.

Vẽ tranh trung thu chị Hằng
Chị Hằng vẫn luôn là hình ảnh quen thuộc trong tâm thức trẻ thơ khi nghĩ về Tết Trung thu. Vậy thì tại sao chúng ta không tận dụng nó cùng sự sáng tạo của trẻ để giúp trẻ làm nên những bức tranh xinh đẹp nhỉ?

Chị Hằng một mình nơi cung trăng ngắm nhìn trẻ em và người người nô đùa náo nức.

Chị Hằng rời khỏi cung trăng, dắt theo chú thỏ nhỏ đáng yêu của mình để đón trung thu cùng với các em thiếu nhi trong không khí tưng bừng và rộn ràng.

Vẽ tranh trung thu bằng màu nước
Màu nước là một loại màu thú vị. Tuy nhiên để có thể làm chủ được cọ vẽ và các màu pha thì các bé cũng phải có một kỹ thuật nhất định để không làm hư tác phẩm của mình. Phụ huynh hãy hỗ trợ bé làm quen nhé!

Tuy khá khó nhưng hiệu ứng mà màu nước mang lại thật không thể chê vào đâu được!

Màu nước sẽ tạo nên được lớp màu đều hơn, tô cũng nhanh hơn và màu sắc thường sặc sỡ hơn.

Vẽ tranh trung thu anime
Trung thu là truyền thống không chỉ của riêng Việt Nam mà của cả các nước phương Đông. Vậy nên các em có niềm yêu thích với văn hóa Nhật Bản có thể giao thoa văn hóa, phong cách vẽ anime cùng ý tưởng Trung thu để tạo nên những bức tranh đặc biệt.

Bên cạnh việc vẽ khung cảnh vui chơi của lớp thiếu thiếu nhi trong mùa trung thu náo nhiệt, sao ta lại không vẽ khung cảnh mọi người cùng chia sẻ niềm vui tới những các em kém may mắn hơn? Đây cũng là một cách lan tỏa tình yêu thương trong cộng đồng thông qua những bức tranh giản dị.

Chúng ta cùng ngắm nhìn hình ảnh chú Cuội thông qua nét vẽ của phong cách anime. Thật sự trông rất thú vị và mới lạ đúng không?

Vẽ tranh trung thu đơn giản mà đẹp
Tuy nhiên không cần cầu kì thì bức tranh mới được đánh giá là đẹp, chúng ta cũng có thể vẽ tranh từ những ý tưởng đơn giản nhất và nét vẽ ngô nghê nhất để hình thành nên những tác phẩm xinh đẹp.

Hình ảnh đơn giản sẽ không bao giờ trở nên nhàm chán nếu như các em có thể phối thêm những sắc màu sặc sỡ. Làm gợi lên được một không gian với không khí rộn ràng, nhộn nhịp, lan tỏa đến cho người xem.

Trong trung thu, bên cạnh những chiếc lồng đèn với ánh lửa huyền ảo, chúng ta không thể thiếu đi hình ảnh của những chú lân vui nhộn và ông địa dẫn vào đi quanh khắp phố phường nhỉ?

Vẽ tranh trung thu mùa covid-19
Nghệ thuật sẽ phần nào phản ánh được hiện thực. Covid có thể mang đến nỗi đau và mất mát cho chúng ta. Thế nhưng không vì thế mà chúng ta lại bỏ qua niềm vui như những hoạt động trung thu thường niên. Thay vì ngồi than khóc cho những việc đã qua, tại sao chúng ta không thông qua những bức tranh để tuyên truyền về một mùa trung thu chung tay phòng chống dịch. Hay như là một lời cảm ơn gửi đến y bác sĩ cùng những người đã đứng lên xung phong bảo vệ chúng ta trong thời gian dịch bệnh hoành hành.


Đeo khẩu trang là một trong những cách đơn giản nhất để ngăn chặn dịch bệnh.

Vẽ tranh rước đèn trung thu
Rước đèn trung thu là một hoạt động không thể nào thiếu trong mùa lễ tết thiếu nhi này. Vậy nên chúng ta không khó để bắt gặp các hình vẽ xung quanh chủ đề này. Tuy nhiên không phải vì vậy mà vẽ tranh về rước đèn trung thu sẽ trở nên nhàm chán. Đây vẫn luôn là một đề tài với tràn đầy cơ hội để các em thiếu nhi thử sức mình sáng tạo.



Xem thêm:
- Tổng hợp các cách vẽ học sinh đơn giản, tranh vẽ học sinh đẹp nhất
- 100+ Ý tưởng vẽ tranh bảo vệ môi trường đẹp nhất, sáng tạo, độc nhất
- 50+ Mẫu vẽ trường tiểu học đẹp, sáng tạo, mới nhất
Trên là 50+ Bức vẽ tranh trung thu đẹp, đơn giản, dễ nhất cho học sinh. Mong là những thông tin trên sẽ phần nào giúp phụ huynh cùng các em dễ dàng hơn trong việc hình thành ý tưởng vẽ nên bức tranh trung thu cho riêng mình. Và đừng quên hãy thường xuyên ghé thăm Bamboo School để đọc thêm nhiều thông tin, hình ảnh thú vị và những kiến thức mới lạ xung quanh việc dạy và học của con em chúng ta nhé!
7 cách học bảng cộng trừ lớp 1 nhanh chóng đơn giản hiệu quả nhất
Ba mẹ có thể nhanh chóng thực hiện các phép toán cộng trừ nhưng để hướng dẫn các bé làm quen với toán học thì không phải là chuyện dễ dàng. Bamboo School sẽ chia sẻ với bạn cách học bảng cộng trừ lớp 1. Bảng cộng trừ này sẽ giúp bé hiểu các phép cộng trừ nhanh hơn. Bé có thể tự học toán và gia tăng khả năng phản xạ toán học trong thời gian ngắn tiếp xúc xúc với bảng cộng trừ này.
Bảng cửu chương cộng trừ là gì?
Bảng cửu chương cộng trừ là bảng toán liệt kê các phép tính cộng và phép tính trừ trong phạm vi nhất định. Cụ thể là đối với các em học sinh lớp 1 sẽ dùng bảng cửu chương cộng trừ trong phạm vi từ 1 đến 10. Khi các em lên lớp 2, lớp 3 thì độ khó của bảng cửu chương cộng trừ sẽ tăng dần lên.
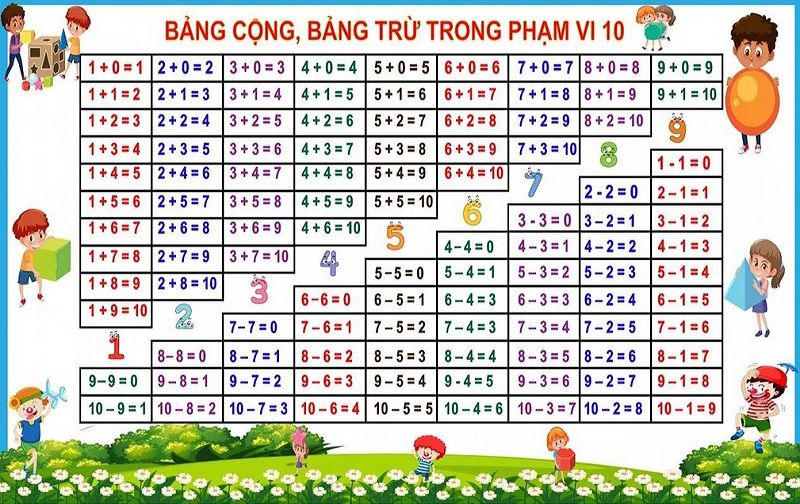
Cách học bảng cộng trừ lớp 1 chuẩn nhất là các bậc phụ huynh nên giúp bé hiểu rõ ý nghĩa của các phép tính cộng và trừ. Không nên để bé thụ động và phụ thuộc vào bảng cộng trừ. Điều này sẽ tránh việc bé học vẹt và tránh việc bé bị mất căn bản toán học khi lên lớp lớn.
Lợi ích của việc học bảng cộng trừ
Về bản chất, bảng cửu chương cộng trừ cũng tương tự như bảng cửu chương nhân chia. Khi bé làm quen với môn toán học bằng bảng cộng trừ sẽ mang lại nhiều lợi ích như:
- Giúp bé làm quen với các phép toán cộng, trừ đơn giản nhanh và hiệu quả nhất.
- Giúp bé có thể tự kiểm tra kết quả các bài tập theo bảng cửu chương cộng trừ.
- Giúp bé rèn luyện khả năng phản xạ nhanh hơn với các phép tính cộng, trừ đơn giản.
Các bảng cộng trừ lớp 1
Bé làm quen với toán lớp 1 bằng cách học bảng cộng trừ lớp 1 còn giúp giáo viên và các bậc phụ huynh tiết kiệm được nhiều thời gian dạy toán cho bé hơn. Dưới đây là các bảng cộng trừ lớp 1 mà ba mẹ nên chuẩn bị cho con.
Bảng cộng trừ lớp 1 trong phạm vi 20
Bảng cộng trừ trong phạm vị 20 sẽ được tách riêng bảng cộng và bảng trừ. Trong đó các phép toán sẽ được sắp xếp khoa học giúp bé dễ dàng tra cứu kết quả khi cần.
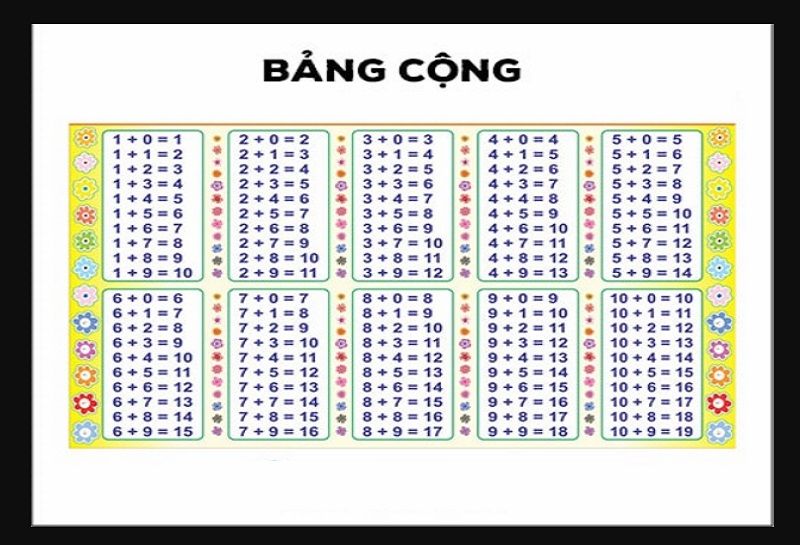

Bảng cộng trừ lớp 1 trong phạm vi 100
Cách học bảng cộng trừ lớp 1 tuy rằng mang lại rất nhiều lợi ích. Tuy nhiên, nếu để bé phụ thuộc vào bảng cộng trừ sẽ làm giảm đi khả năng tư duy toán học. Do vậy, bảng cộng trừ trong phạm vi 100 chỉ được áp dụng phổ thông. Đa phần những bảng cộng trừ trong phạm vi 100 được dùng để đào tạo các bé có năng khiếu toán học.
7 cách dạy trẻ học thuộc bảng cộng trừ nhanh nhất
Dưới đây là các cách học bảng cộng trừ lớp 1 dễ nhất, ba mẹ hãy cùng Bamboo School tham khảo và chọn cho bé cách học phù hợp nhất nhé.
Học cộng trừ trong ngữ cảnh hàng ngày
Bên cạnh cách học bảng cộng trừ lớp 1 bằng các bài tập trên sách vở, ba mẹ có thể cho con học cộng trừ từ các đồ vật quen thuộc sẵn có xung quanh. Như: bát, đũa, ống hút, quyển vở, cây bút,…
- Bước 1: Ba mẹ hãy đặt câu hỏi với bé. “Mẹ đang có 2 cây bút, ba cho mẹ thêm 1 cây bút. Hỏi con, mẹ có bao nhiêu cây bút?”
- Bước 2: Đây là phép toán cộng, mẹ hãy để sẵn 2 cây bút ở phía mẹ và lấy 1 cây bút thêm vào chỗ 2 cây bút sẵn có. Đây là cách giúp bé hiểu đúng bản chất của phép toán cộng.
- Bước 3: Ba mẹ hãy cho con thời gian suy nghĩ để thực hiện phép toán.
- Bước 4: Nếu bé thực hiện phép tính sai, ba mẹ nên kiên nhẫn hướng dẫn con đếm và thực hiện phép toán cộng.
- Bước 5: Ba mẹ hãy lặp lại và nhấn mạnh kết quả bài toán. “Như vậy, đáp án phép tính cộng là 2 + 1 = 3”.

Ba mẹ có thể hướng dẫn bé làm toán trừ với cách làm tương tự như ví dụ trên.
Học cộng trừ bằng hoa quả
Bạn có thể dùng các loại hoa quả thường dùng ở nhà như quả táo, quả chuối, quả nho, quả cam,… để giúp bé học cộng trừ. Cách giúp bé học cách cộng trừ bằng hoa quả cũng tương tự như cách học cộng trừ trong ngữ cảnh.
- Bước 1: Ba mẹ hãy đặt câu hỏi với bé. “Trên bàn đang có 5 quả chuối, con ăn 1 quả chuối. Hỏi trên bàn còn mấy quả chuối?”. Ba mẹ nên lưu ý, số liệu trong các bài toán nên trùng khớp với số lượng hoa quả có sẵn trên bàn.

- Bước 2: Đây là phép toán trừ, ba mẹ hãy lấy 1 quả chuối ra khỏi bàn và đưa về phía con.
- Bước 3: Ba mẹ hãy cho con thời gian suy nghĩ để thực hiện phép toán.
- Bước 4: Nếu bé thực hiện phép tính sai, ba mẹ nên kiên nhẫn hướng dẫn con hiểu về bản chất của phép trừ là giảm bớt đi. Và hướng dẫn bé đếm số quả chuối còn lại trên bàn.
- Bước 5: Ba mẹ hãy lặp lại và nhấn mạnh kết quả bài toán. “Như vậy, đáp án phép tính trừ là 5 – 1 = 4”.
Mách bạn mẹo hay: Những lúc bé phản ứng chậm với kết quả bài toán. Bạn hãy sử dụng bảng cộng trừ để giúp con ghi nhớ nhanh kết quả các phép toán. Đây là cách học bảng cộng trừ lớp 1 giúp bé nhớ nhanh nhất.
Học cộng trừ bằng que tính
Bộ que tinh là một trong những dụng cụ học toán không thể thiếu của học sinh lớp 1. Trong thời gian bé làm bài tập về nhà hoặc tự học tại nhà, ba mẹ nên dùng que tính để bé học bài nghiêm túc hơn.

Ba mẹ chỉ cần áp dụng trình tự các bước hướng dẫn bé học phép tính cộng, trừ mà chúng tôi vừa chia sẻ trên. Đảm bảo bé sẽ học nhanh nhớ lâu và phát triển tư duy toán học hiệu quả.
Học cộng trừ bằng những chiếc kẹo
Đối với các bé có niềm đam mê với kẹo, ba mẹ có thể dùng kẹo để hướng dẫn bé học phép toán cộng trừ. Ba mẹ có thể dùng kẹo làm phần thưởng cho các bài toán đúng.
Đây là cách học bảng cộng trừ lớp 1 theo hình thức vừa học vừa chơi. Giúp kích thích bé hào hứng hơn khi học.
Học cộng trừ bằng đồ chơi
Trong thời gian chơi đồ chơi cùng con, ba mẹ cũng có thể dành khoảng 5 phút để con học phép tính cộng, trừ từ các món đồ chơi này. Ba mẹ có thể chọn các món đồ chơi con có nhiều như xe, viên bi tròn, thẻ ticker, mô hình khủng long,… để giúp con học toán.

Lúc này, ba mẹ hãy khéo léo để những bài toán trở thành những câu đố vui giúp bé hào hứng hơn khi trả lời câu hỏi của ba mẹ.
File bảng cộng trừ lớp 1
Học toán bằng cách học bảng cộng trừ lớp 1 đã mang lại rất nhiều lợi ích thực tiễn. Do vậy, chúng ta có thể mua bảng cộng trừ ở tại các nhà sách, trên các trang thương mại điện tử,….
[su_button url=”https://drive.google.com/file/d/1vmRdQOOpT20ctGL-FLJAkfr4Iw9bfEfO/view?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY FILE BẢNG CỘNG TRỪ LỚP 1[/su_button]
Xem thêm:
- 50+ Cách làm đồ dùng học tập đẹp, cute, đơn giản dễ làm
- Cách chia thời gian học hiệu quả, tối ưu nhất cho học sinh
- Cách học bảng cửu chương hiệu quả, nhớ nhanh, nhớ lâu, đơn giản nhất
Hy vọng với chia sẻ cụ thể về cách học bảng cộng trừ lớp 1 mà Bamboo School vừa chia sẻ trên sẽ giúp ba mẹ hướng dẫn bé học toán dễ dàng hơn. Trên website của Bamboo School còn rất nhiều những mẹo hay giúp bé hăng hái và tích cực học tập hơn. Bạn hãy theo dõi Bamboo để biết thêm nhiều thông tin giáo dục bổ ích.
Ngày 2 tháng 9 là ngày gì? Ý nghĩa và lịch nghỉ ngày 2/9
Là con dân của đất nước Việt Nam chắc hẳn bạn không thể nào không biết đến ngày 2 tháng 9 năm 1945 – đây là ngày vô cùng trọng đại, là cột mốc lịch sử sáng chói và là ngày độc lập dân tộc chấm dứt chế độ thực dân phong kiến tại nước ta. Một kỷ nguyên mới ra đời, kỷ nguyên của độc lập tự do hạnh phúc và chủ nghĩa xã hội bắt đầu.
Ngày 2/9 là ngày gì?
Ngày 2 tháng 9 là ngày gì? Câu trả lời đó chính là ngày Quốc khánh của Việt Nam, là một trong những ngày lễ lớn của năm. Vào ngày 02/09/1945, tại quảng trường Ba Đình – Hà Nội, thay mặt cho Chính phủ lâm thời, Chủ tịch Hồ Chí Minh vĩ đại đã đọc bản Tuyên ngôn độc lập khai sinh ra “Nước Việt Nam Dân Chủ Cộng Hòa” với toàn dân và thế giới. Trong bản tuyên ngôn ấy có khẳng định: “Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng, tính mạng và của cải để giữ vững quyền tự do, độc lập ấy”.

Và thật là điều trùng hợp diệu kỳ trong lịch sử khi sáng ngày 2/9/1696, tại ngôi nhà 67, người Cha già kính yêu của dân tộc đã về cõi vĩnh hằng để lại cho chúng ta một bản di chúc lịch sử là những lời dặn và tình cảm, niềm tin của Người cho thế hệ hôm nay và mai sau.
Ý nghĩa ngày 2/9
Ngày 2/9 là ngày có ý nghĩa vô cùng trọng đại với toàn thể người con đất Việt, là mốc son chói lọi trong hành trình dựng nước và giữ nước của cả dân tộc ta. Kể từ ngày hôm ấy, Việt Nam đã có tên trên bản đồ thế giới và Việt Nam dân chủ Cộng Hòa được ra đời (ngày nay chính là Cộng hòa Xã hội Chủ nghĩa Việt Nam).

Khi bản Tuyên ngôn được cất lên, đồng bào trong và ngoài nước đều một lòng hướng về Tổ Quốc. Ngày hôm ấy chúng ta đã khẳng định cho toàn thế giới biết rằng Việt Nam là một quốc gia hoàn toàn tự do độc lập. Ngày lễ này còn là dịp để mọi người cùng tưởng nhớ đến sự hy sinh vẻ vang, anh dũng của ông ta ngày trước và nhắc nhở cho thế hệ hôm nay và mai sau phải liên tục xây dựng, bảo vệ chủ quyền quốc gia.
Giá trị lịch sử ngày quốc khánh
Ngày 2 tháng 9 là ngày gì và có giá trị lịch sử như thế nào là thắc mắc của nhiều bạn. Ngày Quốc khánh mùng 2/9 mang giá trị lịch sử to lớn, là ngày mà chúng ta thoát khỏi ách tù đày của thực dân phong kiến, trở thành một quốc gia độc lập chủ quyền và lãnh thổ.

Ngày Quốc khánh như một lời nhắc nhở đến thế hệ hôm nay và mai sau cần phải ra sức phấn đấu học tập cũng như rèn luyện hết mình như lời dạy của Bác: “Đâu cần thanh niên có, việc gì khó có thanh niên”. Chúng ta thật sự may mắn khi được sinh ra trong hòa bình, đất nước đang phát triển không phải sống trong chiến tranh loạn lạc thì hãy luôn nhớ về cha ông ta ngày trước đã phải đánh đổi và hy sinh oanh liệt để bảo vệ Tổ quốc trọn vẹn như ngày hôm nay.
Ngày 2/9 được nghỉ mấy ngày?
Theo Khoản 1 và Khoản 3 Điều 112 trong Bộ luật lao động 2019 quy định thì ngày lễ Quốc Khánh sẽ được nghỉ 2 ngày vào 2/9 và 1 ngày trước hoặc sau đó. Năm nay 2/9 rơi vào thứ 6 (nhằm ngày 7/8 âm lịch) nên cán bộ, công chức, viên chức được nghỉ lễ 4 ngày liên tiếp – từ ngày thứ Năm 1/9/2022 đến hết ngày Chủ nhật 4/9/2022 và không phải hoán đổi ngày nghỉ.
 Quy định nghỉ lễ 2/9
Quy định nghỉ lễ 2/9
Quy định nghỉ lễ 2/9 được áp dụng với công nhân viên chức và người lao động thuộc các cơ quan hàng chính, tổ chức chính trị, tổ chức chính trị – xã hội, sự nghiệp. Đối với những cơ quan hay tổ chức không có lịch nghỉ cố định vào thứ 7 và Chủ nhật thì nên xem xét hoạt động và kế hoạch để có lịch nghỉ phù hợp. Với những doanh nghiệp của người lao động bình thường làm việc thứ 7, Chủ nhật hằng tuần thì được nghỉ ngày 1/9 và ngày 2/9.

Xem thêm:
- 1/6 là ngày gì? Ngày 1 tháng 6 là thứ mấy? Nguồn gốc và ý nghĩa ngày quốc tế thiếu nhi
- Ngày 8/3 là ngày gì? Lịch sử và ý nghĩa ngày 8/3
- Thiết kế Tập san 20/10; Chào mừng Ngày phụ nữ Việt Nam
Với những thông tin trên đây có lẽ bạn đã biết được ngày 2 tháng 9 là ngày gì và có ý nghĩa trọng đại như thế nào rồi đúng không nào. Chúc bạn có những ngày nghỉ lễ thật tuyệt vời bên gia đình, người thân và bạn bè nhé!
Cách giải bài toán bằng cách lập phương trình và các dạng bài thường gặp
Hệ phương trình và phương trình đều thuộc vào các dạng kiến thức cơ bản tuy nhiên lại chiếm phần lớn sự quan trọng đối với chương trình môn Toán. Để có hiểu hiểu rõ hơn về các phương pháp lập phương trình và các kiến thức tổng quát nhất trong phương trình, thì sau đây bạn hãy cùng với Bamboo School tìm hiểu về cách giải toán bằng cách lập phương trình và các dạng bài thường gặp nhé!
Tổng quan về phương trình
Trước khi bắt đầu đi sâu vào các phương pháp giải các bài toán qua cách lập phương trình thì chúng ta cần phải thực sự nắm rõ những kiến thức căn bản về phương trình.
Phương trình là gì
Thuật ngữ “Phương trình” có ý nghĩa là dùng để nói tới 2 biểu thức bằng nhau. Trong mỗi một phương trình sẽ gồm có biến số hoặc còn gọi là ẩn. Phương trình sẽ gồm có 2 loại sau:
- Phương trình có điều kiện: đây là dạng phương trình sẽ có ý nghĩa duy nhất với một hoặc cùng với một số có giá trị trong biến số. Bên cạnh đó, phương trình có thể không thích hợp với hầu hết các giá trị khác trong biến số.
- Đồng nhất thức: là một dạng phương trình mang ý nghĩa với tất cả các giá trị của biến số.
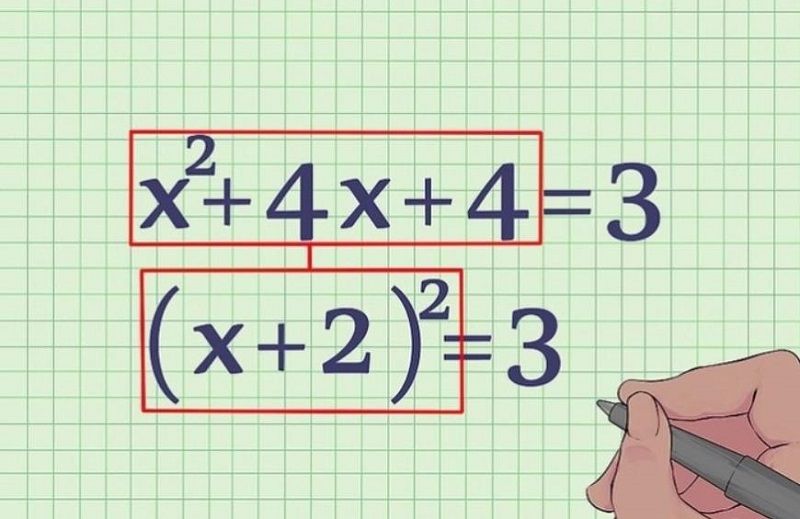
Phương trình cũng như là giải các bài toán bằng cách lập hệ phương trình sẽ là những dạng kiến thức cơ bản nhất để giúp bạn bước đầu tiếp cận dễ dàng những dạng bài tập khác phức tạp hơn thế.
Giải các bài toán bằng cách lập hệ phương trình tức là bạn sẽ cần xác định được chính xác giá trị đúng của những ẩn số để khiến cho phương trình trở nên phù hợp và đúng đắn. Song song đó thì giá trị biến số còn được coi là nghiệm cho phương trình ấy.
Cách trình bày của phương trình là bạn sẽ viết 2 biểu thức ở 2 bên và ở giữa 2 biểu thức sẽ là dấu “=”.
Tác dụng của việc giải bài toán bằng cách phương trình
Phương trình luôn luôn là một nội dung giảng dạy được xem trọng trong chương trình giáo dục. Việc giảng dạy về cách áp dụng phương trình để giải toán sẽ cho học sinh thấy rõ được sự ứng dụng trong thực tế của những lý thuyết về phương trình đối với đời sống.
Trong cấu trúc của các đề thi quan trọng hàng năm hầu hết luôn có giải các bài toán bằng lập phương trình, ngoài ra các đề thi học sinh giỏi cũng thường gồm có nội dung này để xét chọn, vì vậy mà mỗi học sinh cần chú ý nhiều hơn về việc rèn luyện tốt tới việc phát triển các kỹ năng để có thể giải các bài toán bằng cách lập phương trình.

Giải các bài toán bằng phương trình sẽ vô tình rèn luyện nên các khả năng phân tích tình huống, nghiên cứu các bài toán trong các dạng đặc thù và riêng lẻ. Ngoài ra nếu thực hiện tốt kỹ năng sẽ giúp cho học sinh phát huy tư duy một cách linh hoạt, nhạy bén, sáng tạo cho từng bài toán. Các em sẽ không còn trở nên ngại ngùng khi bắt tay giải các bài toán bằng cách lập phương trình nữa mà sẽ cảm nhận được rằng môn toán thực sự gần gũi với các môn hoặc khác và kể cả đời sống thực tế.
Giải các bài toán bằng cách lập phương trình là một trong các hình thức hữu hiệu để dẫn dắt cho học sinh tự tìm hiểu thêm những nền tảng kiến thức khác. Đây cũng là một cách để vận dụng các kiến thức trên sách vở vào trong thực tế, đời sống hàng ngày. Cũng như đây sẽ là một trong những phương pháp kiểm tra năng lực kiến thức của các bạn học sinh cũng như các khả năng tiếp thu và mức độ vận dụng các kiến thức đã được học.

Các bước giải bài toán bằng cách lập phương trình
Để có thể giải một bài toán bằng cách lập phương trình không phải là điều quá phức tạp, để có thể nhanh chóng và dễ dàng thực hiện nhất, bạn hãy thực hiện theo 3 bước sau đây:
Bước 1: Phân tích từng chi tiết trong đề bài
Để dễ dàng đưa ra lời giải nhất thì cách tốt nhất là bạn cần phải thật đọc kỹ đề, hiểu và nắm rõ chúng. Qua đó bạn cần xác định những yếu tố sau đây:
- Xem xét các đại lượng đã có sẵn, những đại lượng cần phải tìm và mối quan hệ liên quan giữa 2 loại đại lượng đó.
- Xác định biến số sao cho phù hợp với đề bài cũng như là xác định các điều kiện đối với biến số.
- Thể hiện các đại lượng khác dựa trên biến số đã được chọn.
- Tiến hành lập phương trình.
Bước 2: Bắt đầu giải phương trình
Tiếp theo đây, dựa vào phương trình đã được lập tại bước 1, bạn hãy xác định chính xác các giá trị cần tìm của biến số sao cho phương trình sẽ có ý nghĩa.
Bước 3: Kết luận
Khi bạn đã tìm ra các nghiệm qua các bước trên thì tiếp theo đây bạn hãy so sánh cùng với những điều kiện đã cho sẵn ở phương trình, điều này sẽ giúp bạn tìm ra đáp án chính xác nhất. Sau khi đã có kết quả, hãy tiến hành đưa ra kết luận của bài toán.
Các dạng bài về cách lập phương trình thường gặp
Giải các bài toán bằng các phương pháp lập phương trình là nhóm kiến thức thường hay gặp trong một số các dạng toán về vận tốc, năng suất hay về liên kết hình học hoặc cũng có thể là số học.
Sau đây là các dạng ghi ví dụ cụ thể dễ hiểu.
Dạng bài về vận tốc
Đây là dạng bài toán để giúp bạn tính được vận tốc cũng có thể là thời gian hoặc là quãng đường qua các tình huống về phương tiện đang di chuyển. Rèn luyện được giải dạng bài toán này bằng các phương pháp lập phương trình với bài toán vận tốc sẽ hỗ trợ bạn rèn luyện kỹ năng quản lý thời gian.

Công thức của dạng bài toán về vận tốc:
S = v.t
Trong đó: S nghĩa là quãng đường, v tức là vận tốc, t sẽ là thời gian.
Để có thể bắt đầu tiến hành tính được vận tốc cũng như là khoảng thời gian có thể di chuyển thì bạn cần dựa trên công thức gốc. Và ngoài ra trong các trường hợp cần tính vận tốc của những phương tiện đang di chuyển dưới nước thì bạn sẽ cần phải dựa trên một công thức khác. Nghĩa là:
- v (xuôi) = v (thực) + v (nước)
- v (ngược) = v (thực) – v (nước)
Bài tập ví dụ cụ thể:
Một chiếc ô tô di chuyển từ Tp.Thủ Dầu Một đến thành phố Hồ Chí Minh với vận tốc 45km/h, rồi khi từ Tp.Hồ Chí Minh quay lại Tp.Thủ Dầu Một cùng với vận tốc là 50km/h. Hãy tính quãng đường bắt đầu từ Tp.Hồ Chí Minh cho đến Tp.Thủ Dầu Một? Với thời gian khi về sẽ ít hơn thời gian khi đi 20 phút.
Giải

Dạng bài về năng suất
Các dạng bài toán về tính năng suất hầu như đều chiếm phần lớn tỷ lệ trong các bài tập giải bằng cách lập phương trình. Công thức về bài toán năng suất như sau:
V = N.T
Trong đó: V tức là khối lượng công việc thực hiện, N nghĩa là năng suất còn T nghĩa là thời gian.
Để có thể dễ dàng tính được thời gian cần thiết để thực hiện công việc cũng như năng suất thực hiện. Qua việc rèn luyện tính toán tốt năng suất sẽ phần nào giúp bạn có thể quản lý tốt hơn công việc của mình.

Bài tập ví dụ cụ thể:
Một người được cấp trên bàn giao hoàn thiện một lượng sản phẩm trong khoảng thời gian. Người ấy định mỗi ngày sẽ làm xong 48 số lượng sản phẩm. Sau một ngày thực hiện, người ấy nghỉ thêm 1 ngày, vì vậy để có thể hoàn thành công việc đúng tiến độ thì mỗi ngày sau đó cần phải tăng thêm 6 sản phẩm. Vậy dựa trên những dữ liệu có sẵn, hãy tính lượng sản phẩm mà ban đầu người đó đảm nhận.
Giải

Dạng bài về liên kết hình học
Những dạng toán có liên quan tới hình học đều sẽ gồm các nội dung về vị trí, kích thước,…Và khi tiến hành giải những bài toán bằng các phương pháp về lập phương trình liên quan đến hình học, thì bạn cần phải chú ý tới một số các công thức khác liên quan tới hình học như tính chu vi hay diện tích,…


Dạng bài về số học
Những bài toán có các nội dung liên quan đến số học đều là các dạng toán có liên quan tới mối quan hệ giữa các số với nhau. Ví dụ như các quan hệ bằng nhau, có thể lớn hơn hoặc là nhỏ hơn hay cũng có thể là các quan hệ đồng dạng hay các quan hệ đồng dư,… Việc bạn tìm ra các ẩn số bằng các phương pháp để giải các bài toán bằng cách lập phương trình sẽ hỗ trợ bạn dễ dàng tìm ra các đáp án cho các biểu thức.

Bài tập ví dụ cụ thể:
Hai số dương có hiệu bằng 22. Biết rằng số này sẽ gấp đôi so với số kia. Hãy tìm ra hai số dương đó.
Giải:
- Số dương thứ nhất gọi là x ( x>0 )
Số dương thứ hai gọi là y ( y>x>0 )
Vì vậy mà ta có: y-x = 22 suy ra y = 22+x
- Theo như dữ liệu đã cho trước thì số này sẽ gấp đôi so với số kia, ta có:
y = 2x ⇔ 22+x = 2x
⇔ 22 = 2x-x ⇔ x=22 ( thỏa mãn điều kiện)
Với x=22 ⇒ y=44
Vậy ta có thể kết luận rằng, hai số dương thỏa mãn điều kiện nhất là 44 và 22.
Xem thêm:
- Cách tính giá trị biểu thức và ví dụ bài tập minh họa có đáp án
- 10 cách học giỏi toán hiệu quả nhất cho người mất gốc
- R trong toán học là gì? Định nghĩa, tính chất và bài tập minh họa có giải
- Các tính tỉ số phần trăm và các dạng toán về tỉ số phần trăm cơ bản có đáp án
Và trên đây là các cách giải bài toán bằng cách lập phương trình và các dạng bài thường gặp, mong rằng những điều mà Bamboo School chia sẻ tới cho các bạn sẽ hỗ trợ phần nào cho quá trình học tập và rèn luyện của các bạn. Chúc các bạn sẽ ôn tập hiệu quả và gặt hái được kết quả hơn mong đợi.
7 cách học sử hiệu quả nhanh chóng cho học sinh
Như thế nào là cách học sử hiệu quả? Tại sao môn sử lại khó học thuộc hơn các môn khác? Cần lưu ý những gì khi học môn sử? Đây có lẽ là thắc mắc chung của nhiều giáo viên và học sinh. Bài viết dưới đây sẽ giới thiệu đến các bạn 7 cách học sử hiệu quả và nhanh chóng mà bất cứ ai cũng có thể áp dụng.
Lý do khiến bạn học sử “khó”
Trong tất cả các môn học, môn sử luôn được xem là môn học “khó nuốt” nhất. Để học giỏi Lịch sử không phải là điều dễ dàng. Bạn cần phải đầu tư nhiều thời gian, công sức, đồng thời phải tìm ra phương pháp học phù hợp thì mới có thể đạt kết quả cao trong học tập. Sở dĩ, việc học sử luôn trở thành nỗi lo lắng của nhiều học sinh trước hết là do bản chất của môn học này vốn có nhiều sự kiện lịch sử, mốc thời gian khác nhau. Đối với từng mốc thời gian cụ thể, bạn phải ghi nhớ thật chính xác và học thuộc nó. Điều này khiến cho người học cảm thấy “choáng ngợp” và dễ bị nhầm lẫn giữa các sự kiện với nhau. Nếu chỉ học thuộc trong một thời gian ngắn thì bạn không thể nào ghi nhớ toàn bộ các sự kiện quan trọng, dẫn đến tình trạng học vẹt, học trước quên sau.
Bên cạnh đó, để học tốt Lịch sử, chúng ta còn phải rèn khả năng tư duy nhạy bén, lập luận rõ ràng. Sai lầm phổ biến của nhiều học sinh hiện nay đó là cho rằng, học sử chỉ cần học thuộc là được. Chính điều này đã kìm hãm người học không thể tìm ra cách học sử hiệu quả và phù hợp. Lâu dần, học sinh dần đánh mất niềm đam mê đối với môn Lịch sử, và hầu như chỉ có một phương pháp học duy nhất là học thuộc để vượt qua các bài kiểm tra, kỳ thi cuối kỳ.

Hiện nay, nhiều học sinh vẫn chưa tìm ra cách học sử hiệu quả và phù hợp với bản thân
Tại sao chúng ta cần phải học lịch sử?
Lịch sử chính là nền tảng, là cái “gốc” của nước nhà. Bên cạnh các môn học chính là Toán, Ngữ văn và tiếng Anh, thì Lịch sử cũng đóng một vai trò quan trọng không thể thiếu trong việc giáo dục học sinh. Học sử trước hết là học về quá trình dựng nước và giữ nước của cha ông, biết được nguồn gốc hình thành nước nhà, những cuộc kháng chiến bảo vệ Tổ quốc. Từ đó, hình thành nên ở mỗi người nhận thức đúng đắn về đất nước, về lịch sử của các thế hệ cha ông.
Học sử không chỉ giúp chúng ta trau dồi tri thức, vốn hiểu biết mà còn giáo dục lòng yêu nước, lòng tự tôn dân tộc. Thông qua quá trình tìm hiểu về lịch sử, chúng ta sẽ học hỏi được những truyền thống, giá trị tốt đẹp của dân tộc. Đồng thời, ta sẽ có nhận thức, trách nhiệm tiếp tục gìn giữ, bảo tồn và phát huy những giá trị truyền thống đó, tiếp bước các thế hệ đi trước.

Học lịch sử không chỉ để tìm hiểu về quá trình dựng nước và giữ nước, mà còn để hiểu hơn về những truyền thống tốt đẹp của dân tộc
Nguyên tắc để học giỏi môn Lịch sử
Học tập là một hành trình lâu dài chứ không phải diễn ra chỉ trong ngày một ngày hai. Để học tốt môn Lịch sử, ngoài việc tìm ra cách học phù hợp thì bạn còn phải nắm rõ 4 nguyên tắc sau đây.
Phân bổ thời gian hợp lý
Một trong những cách học sử hiệu quả mà bạn có thể áp dụng đó là phân bổ thời gian hợp lý. Đối với từng môn học, bạn nên lập ra thời gian biểu cụ thể và thực hiện theo đúng kế hoạch đã lập. Không phải môn học nào cũng có thời gian học giống nhau. Việc phân chia thời gian học hợp lý sẽ giúp bạn tập trung cao độ trong học tập, đồng thời không làm ảnh hưởng đến thời gian học các môn khác.
Phân bổ thời gian hợp lý là một trong những cách học sử hiệu quả nhất
Chọn thời điểm học phù hợp
Không phải cứ học liên tục, học nhiều giờ đồng hồ trong một ngày là bạn có thể giỏi Lịch sử một cách nhanh chóng. Đó không phải là cách học sử hiệu quả. Bạn hãy lựa chọn ra thời điểm phù hợp nhất trong ngày để ôn tập kiến thức Lịch sử. Thời điểm mà đầu óc bạn minh mẫn, có năng lượng nhất là vào buổi sáng sớm. Bạn có thể tranh thủ khoảng thời gian này để đọc tài liệu, tìm hiểu các sự kiện lịch sử và làm các bài tập của môn học. Nên hạn chế học ở thời điểm bạn cảm thấy mệt mỏi, chán nản vì đây là lúc cơ thể cần được nghỉ ngơi, thư giãn.

Bạn không nên học quá nhiều trong một ngày mà chỉ nên lựa chọn thời điểm phù hợp nhất để học lịch sử
Chia thông tin theo từng phần để ghi nhớ
Kiến thức Lịch sử là vô cùng rộng lớn. Nó bao hàm nhiều sự kiện, nhân vật, mốc thời gian khác nhau,… Do đó, bạn không thể nào ghi nhớ hết toàn bộ thông tin chỉ trong một thời gian ngắn. Việc gượng ép bản thân phải ghi nhớ quá nhiều kiến thức cùng một lúc sẽ chỉ khiến bạn cảm thấy chán nản và mất động lực học tập. Thay vào đó, bạn nên chia khối lượng kiến thức thành từng phần nhỏ, rồi học kỹ từng phần.
Đối với từng chương, từng phần nhỏ, bạn có thể kết hợp với việc làm bài tập, đọc tài liệu nâng cao, sử dụng giấy note,… để tăng khả năng ghi nhớ. Đây cũng là một cách học sử hiệu quả mà bạn nên tham khảo.

Nên áp dụng phương pháp chia nhỏ nội dung để học sử hiệu quả
Nghỉ ngơi đúng lúc
Học nhiều chưa chắc đã hiệu quả bằng việc học và nghỉ ngơi đúng thời điểm. Sau những giờ học căng thẳng, bạn cũng nên dành thời gian để thư giãn về tinh thần. Bạn không nên gượng ép bản thân phải học trong trạng thái uể oải, mệt mỏi. Bạn có thể đọc sách, nghe nhạc, xem phim, đi dạo, tập thể dục,… hoặc làm những việc mà bạn yêu thích trong thời gian nghỉ ngơi. Điều đó sẽ giúp bạn lấy lại năng lượng để tiếp tục học tập và làm việc hiệu quả.

Trong số những cách học sử hiệu quả, bạn không nên bỏ qua nguyên tắc nghỉ ngơi đúng thời điểm
Những cách học giỏi Lịch sử hiệu quả, nhanh chóng
Sau khi đã tìm hiểu 4 nguyên tắc quan trọng để học tốt môn Lịch sử, chắc hẳn các bạn đã phần nào suy nghĩ ra những phương pháp học phù hợp dành cho bản thân. Dưới đây là 7 cách học sử hiệu quả mà bạn nên ghi nhớ và thực hiện theo.
Đọc lại bài cũ vào mỗi buổi tối
Phương pháp đầu tiên trong những cách học sử hiệu quả đó là bạn phải ôn tập, đọc lại bài cũ vào mỗi buổi tối. Nếu chỉ học ở trên lớp mà không dành thời gian tự học ở nhà thì bạn rất dễ rơi vào tình trạng học trước quên sau. Bạn không cần phải học thuộc hết toàn bộ kiến thức mà có thể đọc tài liệu nhiều lần. Như vậy, não bộ sẽ dần hình thành khả năng ghi nhớ thông tin một cách chắc chắn.
Tiếp tục duy trì phương pháp này trong thời gian dài sẽ giúp bạn tạo lập một thói quen tốt. Bên cạnh đó, việc thường xuyên đọc lại bài cũ vào buổi tối còn giúp bạn giảm bớt gánh nặng, khối lượng kiến thức trong mỗi kỳ thi. Bởi vì lúc này, não bộ của bạn đã ghi nhận rất nhiều thông tin, và bạn cũng không cần phải ôn tập lại quá nhiều trước mỗi lần thi cử.
Đọc bài mới trước khi đến lớp
Ngoài việc ôn tập lại bài cũ thì bạn cũng cần chuẩn bị bài mới trước khi đến lớp. Nhiều học sinh chủ quan khi cho rằng, chỉ cần đến lớp nghe giảng là có thể hiểu được bài vở. Thực ra, học sử đòi hỏi một quá trình tìm hiểu kiến thức trong thời gian dài. Nếu bạn không có sự chuẩn bị từ trước thì khi đến lớp, bạn rất dễ bị choáng ngợp trước khối lượng thông tin, các mốc thời gian, sự kiện có trong bài.
Từ đó dẫn đến đến việc tiếp thu kiến thức trở nên kém hiệu quả. Bạn nên dành ít nhất 20 – 30 phút để đọc trước bài mới ở nhà. Là, như vậy sẽ giúp bạn nhanh hiểu bài hơn, và việc nắm bắt kiến thức trên lớp cũng trở nên tốt hơn.

Một cách học sử hiệu quả mà bạn nên áp dụng đó là dành từ 20 – 30 phút đọc bài mới trước khi đến lớp
Học thuộc bằng cách ghi chép thay vì đọc nhẩm
Không chỉ riêng môn sử mà đối với bất kỳ môn học nào, chỉ học kiến thức suông thì rất khó để ghi nhớ lâu dài. Nếu bạn chỉ đọc nhẩm các sự kiện, mốc thời gian thì càng dễ làm cho bạn cảm thấy buồn ngủ và khó tập trung. Thay vào đó, bạn nên ghi chép những ý chính ra vở. Mỗi lần ghi chép là mỗi lần não bộ tiếp nhận lại thông tin đã có sẵn.
Bạn có thể áp dụng áp dụng phương pháp này bằng cách đọc qua bài học vài lần, sau đó viết ra vở những nội dung mà bạn cho là trọng tâm. Ngoài ra, bạn cũng có thể viết những từ khóa, sự kiện quan trọng lên giấy note rồi dán ở vị trí bàn học. Đây là một cách học sử hiệu quả dành cho những ai muốn đạt kết quả cao trong môn học này.

Bạn nên tập cho mình thói quen ghi chép lại những nội dung chính của bài học
Đọc hiểu nhớ bài thay vì học vẹt
Khi học Lịch sử, bạn nên ghi nhớ một điều: Học vẹt chỉ có tác dụng tạm thời, giúp bạn đối phó với các bài kiểm tra trước mắt. Nó không có hiệu quả lâu dài vì rất dễ khiến cho người học quên đi kiến thức một cách nhanh chóng. Cho nên, sau mỗi kỳ thi, lượng kiến thức mà bạn cần phải ôn tập lại sẽ càng nhiều hơn. Chính vì vậy, bạn nên bỏ thói quen học vẹt.
Để việc học môn sử trở nên dễ dàng và hiệu quả hơn, bạn nên rèn cho mình phương pháp đọc hiểu. Bạn có thể chia bài học thành từng mục nhỏ khác nhau. Trước hết, bạn hãy đọc toàn bộ bài học để hiểu được nội dung chính được đề cập trong sách, sau đó gạch chân những từ khóa, kiến thức quan trọng. Với mỗi nội dung bài học, bạn cần phải nắm chắc ý nghĩa, bản chất của vấn đề, sự kiện.

Đọc hiểu bài học cũng là một cách học sử hiệu quả
Học theo sơ đồ tư duy
Học bằng sơ đồ tư duy cũng là một cách học sử hiệu quả được rất nhiều giáo viên và học sinh áp dụng trong quá trình giảng dạy và học tập. Hãy biến những con chữ, số liệu khô khan trên trang sách thành những hình ảnh trực quan, sinh động và bắt mắt. Điều này sẽ kích thích khả năng tư duy, sáng tạo, cũng như khơi dậy niềm đam mê, hứng thú của người học đối với môn Lịch sử.
Chỉ với một trang giấy A4, những ngòi bút bi nhiều màu là bạn đã có thể tự sáng tạo nên sơ đồ tư duy theo sở thích của mình. Tuy nhiên, trước khi vẽ sơ đồ tư duy, bạn cũng cần phải đọc qua bài học nhiều lần và nắm chắc thông tin, đồng thời chắt lọc, lựa chọn ra những từ khóa và nội dung chính để biểu thị bằng các hình vẽ.
Sử dụng sơ đồ tư duy là một cách học sử hiệu quả và thú vị mà bạn nên tham khảo
Xem thêm các tài liệu lịch sử qua phim ảnh
Học lý thuyết phải đi đôi với thực tế. Nếu chỉ học kiến thức suông trong sách vở thì sẽ rất khô khan và nhàm chán. Bạn có thể đổi mới “tài liệu học tập” của mình bằng cách xem những bộ phim, tranh ảnh liên quan đến lịch sử nước nhà. Đây cũng là một cách học sử hiệu quả và đem đến những giây phút thư giãn cho người học. Đối với phương pháp này, bạn có thể vừa học vừa chơi. Thông qua những thước phim về lịch sử, người học sẽ có hình dung chân thực và rõ nét hơn về quá trình xây dựng và bảo vệ đất nước của cha ông, từ đó khơi gợi niềm đam mê, hứng thú đối với môn học này.

Thông qua những thước phim về lịch sử, người học sẽ có những hình dung chân thực và rõ nét hơn về quá trình xây dựng và phát triển đất nước của các thế hệ đi trước
Học sử qua các ứng dụng mạng xã hội
Ngoài những phương pháp trên, bạn cũng có thể áp dụng một cách học sử hiệu quả và thú vị, đó là sử dụng các ứng dụng mạng xã hội như: Facebook, TikTok, Instagram, Youtube. Mỗi ứng dụng đều có những tính năng nổi bật riêng. Ví dụ, khi sử dụng Facebook hay Instagram, bạn có thể nhấn theo dõi các fanpage, blog cung cấp kiến thức về lịch sử. Hoặc với Youtube hay TikTok, bạn có thể xem các video, tranh ảnh giới thiệu về các mốc sự kiện, các nhân vật quan trọng trong lịch sử.
Các trang mạng xã hội có thể cung cấp cho người học nhiều kiến thức mới mẻ và thú vị mà không có trong sách vở. Bên cạnh đó, bạn cũng có thể giao lưu, kết bạn, tham gia những cộng đồng, hội nhóm học tập để trao đổi phương pháp học tập hiệu quả đối với tất cả các môn học.

Sử dụng mạng xã hội đúng cách sẽ là một cách học sử vô cùng hiệu quả
Những lưu ý để học sử hiệu quả
Học sử sẽ trở nên dễ dàng và thú vị hơn nếu chúng ta biết tìm ra phương pháp học đúng đắn và khoa học. Để áp dụng những cách học sử hiệu quả, bạn cần lưu ý một số điều dưới đây:
- Luôn luôn nắm vững kiến thức nền tảng, cơ bản trước khi tìm hiểu các kiến thức nâng cao.
- Khi có thắc mắc liên quan đến bài học, cần trao đổi với giáo viên để được giải đáp chi tiết.
- Bạn có thể học nhóm cùng với bạn bè để nâng cao hiệu quả học tập.
- Từ những phương pháp được gợi ý ở trên, bạn cũng có thể tự sáng tạo ra cách học khác, sao cho phù hợp với khả năng của bản thân và có thể khơi dậy động lực học tập.
- Đối với phương pháp ghi chép kiến thức, bạn nên rèn cho mình thói quen ghi chép một cách bài bản, cụ thể và khoa học, để có thể phân biệt được đâu là ý chính, ý phụ một cách dễ dàng.
- Học lịch sử không đơn thuần chỉ là học thuộc, mà bạn còn phải rèn luyện khả năng tư duy, suy luận, lập luận. Có như vậy thì bạn mới có thể hiểu rõ bản chất và ý nghĩa của từng vấn đề, sự kiện khác nhau.
- Điều quan trọng nhất khi học bất cứ môn học nào đó là phải tạo được niềm đam mê, hứng thú và động lực đối với môn học đó. Nếu bạn không có niềm yêu thích đối với môn sử, chỉ học để đối phó với các bài kiểm tra, các kỳ thi trên lớp thì rất dễ chán nản và bỏ cuộc. Việc học cũng vì thế mà trở nên kém hiệu quả.

Dù học bất cứ môn học nào, bạn cũng cần phải có đam mê, niềm yêu thích đối với môn học đó. Đây là một yếu tố quan trọng để bạn áp dụng những cách học sử hiệu quả
Xem thêm:
- 2 cách học tập hiệu quả của người Nhật bạn nên biết
- 10 cách học giỏi toán hiệu quả nhất cho người mất gốc
- 9 Cách học văn hiệu quả, nhanh thuộc, nhớ lâu, không buồn ngủ
Trên đây là tổng hợp 7 cách học sử hiệu quả và nhanh chóng nhất dành cho học sinh mà bạn có thể tham khảo và áp dụng theo. Chúc bạn lựa chọn được phương pháp học tập phù hợp và đạt kết quả cao trong các môn học.
Tổng hợp các cách vẽ học sinh đơn giản, tranh vẽ học sinh đẹp nhất
Vẽ tranh không chỉ đem lại sự sáng tạo, nâng cao trí tuệ mà còn giúp các bạn học sinh có thêm cái nhìn mới mẻ về cuộc sống xung quanh. Những nét vẽ hồn nhiên về đề tài học sinh luôn mang lại sự thu hút với cho người xem. Dưới đây là tổng hợp những cách vẽ học sinh đơn giản, một chủ đề đơn giản mà ý nghĩa cho các bé.
Vẽ học sinh đang nhảy dây
Trò chơi nhảy dây là một trò chơi dân gian gắn liền với bao thế hệ học trò chúng ta. Hầu như các bạn học sinh đều từng chơi trò này. Và để khắc họa lại kỉ niệm lúc nhỏ thì đề tài học sinh nhảy dây luôn được các bạn vẽ lại một cách chân thực và sinh động nhất. Vẽ về đề tài này không chỉ là giải trí hay nâng cao khả năng vẽ tranh mà còn thể hiện được nét đẹp của trò chơi dân gian Việt Nam.


Vẽ học sinh mặc áo dài
Từ xưa đến nay, chiếc áo dài luôn là trang phục truyền thống mang vẻ đẹp hoài cổ của nước ta. Áo dài làm cho những nữ sinh thêm phần trẻ trung, duyên dáng và xinh đẹp hơn. Những cách vẽ học sinh đơn giản thì không thể nào thiếu được hình dáng của những tà áo dài trong sân trường, tất cả được khắc họa chân thực tạo nên nhiều cảm xúc cho người xem tranh.


Vẽ học sinh đi xe đạp
Xe đạp không chỉ là phương tiện đi lại của mọi người mà còn là một phần trong nghệ thuật thị giác nói chung. Vậy nên không quá khó khi thấy những tác phẩm về chiếc xe đạp. Và học sinh đi xe đạp cũng là một trong những đề tài mà các bạn thường hay lựa chọn để vẽ. Nếu như bạn đang muốn vẽ về đề tài này nhưng bị bí ý tưởng thì có thể tham khảo dưới đây nhé.


Vẽ học sinh chào cờ
Nghi thức chào cờ là buổi lễ quan trọng mỗi thứ 2 đầu tuần. Thông qua buổi lễ này các bạn sẽ biết được thành tích của các lớp tuần qua hay những kiến thức mới, chủ điểm sinh hoạt trong tuần, trong tháng. Hầu như các bạn học sinh đều mong chờ buổi lễ này trong tuần và đã vẽ nên những bức tranh về lễ chào cờ vô cùng trang trọng và ấn tượng.


Vẽ học sinh đi học
Mỗi ngày tới lớp đều là một ngày vui nên đề tài học sinh đi học luôn mang màu sắc vô cùng tươi sáng. Nếu như các bạn đang tìm hiểu về cách vẽ học sinh đơn giản thì hãy vẽ cảnh học sinh đi học nhé. Chỉ cần vẽ những cô cậu học trò trong bộ đồng phục xinh xắn khoác trên vai chiếc cặp tung tăng đến trường là bạn đã có bức tranh đẹp rồi đấy.


Vẽ học sinh ngồi đọc sách
Với cuộc sống hiện đại như hiện nay thì việc phát triển văn hóa đọc cho các bạn học sinh là một điều quan trọng và hết sức cần thiết. Một trong những cách tuyên truyền việc đọc sách mà nhà trường lựa chọn đó là vẽ tranh về chủ đề này. Tuy không phải là chủ đề mới mẻ nhưng lại đem lại hiệu quả cao trong việc giúp các bạn chủ động đọc sách, khám phá nhiều kiến thức mà sách mang lại.


Vẽ học sinh ngồi học
Một trong những cách vẽ học sinh đơn giản đó chính là vẽ học sinh đang ngồi học. Không chỉ khắc họa được nét đẹp của các bạn mà còn thể hiện được tình cảm giữa thầy trò thân thương. Chủ đề này có khá nhiều ý tưởng để bạn lựa chọn và thường thì các bạn hãy chọn vẽ lại những khoảnh khắc vui vẻ trên lớp hoặc là những lúc các bạn tập trung học hành, nghề giáo viên giảng bài.


Vẽ học sinh đi học đơn giản
Trường học luôn là đề tài vẽ tranh khá hot bởi đây là nơi ươm mầm tương lai cho đất nước với những bài học hay kiến thức bổ ích. Đến trường là một phần không thể thiếu trong cuộc đời của mỗi người và để giúp các bạn học sinh thể hiện tình cảm của mình khi đi học thì giáo viên thường hay ra đề tài vẽ tranh này và đã có rất nhiều tác phẩm đầy sinh động được ra đời bởi các bạn nhỏ.


Vẽ học sinh nam
Khi nói đến vẽ tranh về đề tài trường học thì không thể nào thiếu những bức tranh vẽ về học sinh. Vẽ học sinh nam thường sẽ được các bạn trai lựa chọn và phát triển những nét vẽ ở nhiều chủ đề như: học sinh nam chơi đá cầu, học sinh nam chơi đá bóng, học sinh nam cùng nhau đọc sách….


Vẽ học sinh tặng hoa cho cô giáo
Không quá khó để vẽ những bức tranh về đề tài này. Những bó hoa mà các bạn thường tặng cô giáo đó chính là bó hoa điểm 10 vì thầy cô nào cũng cảm thấy tự hào khi học trò của mình đạt điểm số tốt. Cách vẽ học sinh đơn giản nhưng để lại ấn tượng trong lòng người ngắm tranh đó là về chủ đề này. Những bông hoa điểm 10 sẽ luôn là một món quà vô giá mà học trò trao tặng cho cô.


Vẽ học sinh nữ
Ngoài những bức tranh về chủ đề học sinh nam nói trên thì vẽ học sinh nữ sẽ được các bạn gái lựa chọn. Học sinh nữ thì thường sẽ khó vẽ hơn học sinh nam về khuôn mặt, đồng phục hay mái tóc. Nếu bạn cảm thấy hơi khó vẽ thì hãy luyện tập thường xuyên để việc vẽ về chủ đề này đơn giản hơn nhé.


Vẽ học sinh đang quét rác
Ngoài những bức tranh về đề tài lớp học, đến trường thì đề tài học sinh bảo vệ môi trường cũng được nhiều bạn lựa chọn. Học sinh đang quét rác là một trong những cách vẽ học sinh đơn giản mà bạn có thể tham khảo. Không chỉ thể hiện tài năng vẽ tranh, sự khéo léo qua cách tô màu mà đề tài này còn giúp tuyên truyền đến nhiều người về ý thức bảo vệ môi trường xung quanh.


Xem thêm:
- 100+ Ý tưởng vẽ tranh bảo vệ môi trường đẹp nhất, sáng tạo, độc nhất
- 40+ cách trang trí vở học sinh đẹp, cute, đẹp nhất, đơn giản dễ làm
- 100+ cách trang trí bàn học đẹp, gọn gàng, cute, kiểu Hàn Quốc
Hi vọng với những chia sẻ về cách vẽ học sinh đơn giản trên đây đã giúp bạn có thêm những ý tưởng mới của riêng mình rồi phải không nào. Chúc bạn có những bức tranh thật đẹp và ấn tượng nhé!
5 Bước lập kế hoạch học tập cho học sinh, sinh viên hiệu quả nhất
Lập kế hoạch luôn là bước gần như không thể thiếu cho bất cứ việc gì trong cuộc sống. Đặc biệt, đối với việc học tập, đây là công đoạn không thể thiếu. Tuy nhiên từng kiến thức khác sau, mục tiêu học tập khác nhau, làm sao để có thể lên kế hoạch một cách phù hợp và đạt được kết quả cao nhất? Vậy thì hôm nay chúng ta cùng điểm qua 5 bước lập kế hoạch học tập cho học sinh, sinh viên hiệu quả nhất để các bạn cũng như là các phụ huynh tham khảo cho chính bản thân hoặc cho con em mình nhé!
Xác định mục tiêu học tập ngắn hạn và dài hạn
Tại sao bước đầu tiên lại là xác định mục tiêu học tập ngắn hạn và dài hạn? Đó là vì việc xác định mục tiêu được coi như là việc định hướng giúp bạn đưa ra được lối học tập phù hợp với bản thân. Bên cạnh đó, mục tiêu sẽ được chia ra thành các mục tiêu ngắn hạn và dài hạn. Những mục tiêu ngắn hạn sẽ là tiền đề giúp bạn hoàn thành mục tiêu dài hạn. Và cũng chính những mục tiêu dài hạn, lại là động lực lớn mạnh nhớ để bạn vượt qua từng mục tiêu nhỏ ngắn hạn bên trong.

Sắp xếp mức độ ưu tiên hợp lý cho từng hoạt động
Tuy nhiên, thông thường trong công cuộc học tập của học sinh và sinh viên hay cả người đã đi làm, chúng ta không chỉ học riêng lẻ một môn học. Thay vào đó, mỗi người chúng ta luôn phải liên tục tiếp thu các loại, các nguồn và các dạng kiến thức khác nhau. Vậy nên sẽ có nhiều mục tiêu khác nhau được đặt ra. Vấn đề ở đây là bạn phải thực hiện việc nào trước?
Đó là nguyên nhân sau khi đã xác định được mục tiêu, bạn phải phân loại và sắp xếp được mức độ ưu tiên cho từng hoạt động. Bạn có thể thực hiện theo ma trận ra quyết định của Eisenhower
| Khẩn cấp | Không khẩn cấp | |
| Quan trọng | (1) | (2) |
| Không quan trọng | (3) | (4) |
Thứ tự ưu tiên cho từng hoạt động của bạn sẽ là (1) -> (2) -> (3) -> (4)

Kiên trì theo sát kế hoạch học tập
Đây được coi là bước khó thực hiện nhất trong 5 bước lập kế hoạch học tập. Vì nó hoàn toàn phụ thuộc vào tính tự giác của bạn. Để có thể kiên trì theo sát kế hoạch học tập, bạn có thể chủ động viết những gì bản thân cần làm vào đầu ngày, đầu buổi và viết những gì mà bạn đã làm được trong ngày hôm đó.

Việc này không chỉ giúp bạn dễ dàng theo sát kế hoạch, không bị lỡ mất bất kỳ deadline hay những đề mục quan trọng nào. Ngoài ra, cách này còn giúp bạn làm động lực để tự thúc đẩy bản thân, từ đó có thể theo sát quá trình một cách dài lâu và trọn vẹn.
Cân bằng thời gian học và các hoạt động giải trí
Học tập là một việc tốt cũng như là nên thực hiện một cách thường xuyên và lâu dài. Tuy nhiên không phải vì như vậy mà bạn dành trọn vẹn thời gian chỉ cho việc học và làm việc. Việc này sẽ khiến cho đầu óc bạn bị quá tải và sẽ giảm hiệu quả tiếp thu một cách đáng kể. Từ đó sẽ làm hao tổn không chỉ sức lực của bản thân từ thể chất đến tinh thần mà còn tốn cả thời gian.

Do vậy, bên cạnh việc lập thời gian cho việc học tập và làm việc, bạn cũng cần chừa ít thời gian cho các hoạt động vui chơi giải trí nhằm cân bằng được tần suất làm việc của não lẫn cơ thể. Từ đó mới mang lại được kết quả cao nhất.
Sử dụng phần mềm lập kế hoạch
Trello
Nếu như bạn là sinh viên đại học hoặc là học sinh cấp 3 chắc cũng đã nghe qua phần mềm Trello. Đây là phần mềm giúp không chỉ cá nhân mà cả tập thể tham gia lập và theo dõi kế hoạch. Với giao diện tương đối đơn giản, dễ hiểu và không tốn phí – Trello chắc chắn là phần mềm mà bạn nên thử.
Ưu điểm:
- Dễ điều chỉnh
- Giao diện thân thiện.
- Miễn phí.
Nhược điểm:
- Khi xóa task không có thông báo, bất cập khi sử dụng theo nhóm.
Linh tải:
Notion
Notion là một phần mềm đa năng. Bạn vừa có thể sử dụng Notion để lập kế hoạch, ghi chú bài học hay thậm chí làm portfolio, CV,… một cách vô cùng đẹp mắt và thỏa sức sáng tạo.
Ưu điểm:
- Đa dạng.
- Miễn phí.
Nhược điểm:
- Phức tạp so với người mới bắt đầu vì có quá nhiều tính năng.
Linh tải

Cloudoffice
So với Trello và Notion, Cloudoffice sẽ kém nổi tiếng hơn. Tuy nhiên nếu như bạn làm việc nhóm thì đây là phần mềm phù hợp nhất khi người dùng có thể theo dõi các task, nhiệm vụ được giao và phân loại, phê duyệt, xem theo ngày/ tuần/ tháng,… hay đặt ra hạn chót có kèm theo thông báo cho mọi người hoặc những người cần thiết.
Ưu điểm:
- Quản lý tài liệu một cách khoa học.
- Phân cấp thành viên tham gia.
Nhược điểm:
- Có tính phí
Linh tải:
Xem thêm:
- Cách chia thời gian học hiệu quả, tối ưu nhất cho học sinh
- 2 cách học tập hiệu quả của người Nhật bạn nên biết
- 10 cách học giỏi toán hiệu quả nhất cho người mất gốc
Trên là thông tin về 5 bước lập kế hoạch học tập cho học sinh, sinh viên hiệu quả nhất. Và mong rằng những thông tin mà Bamboo School chia sẻ sẽ phần nào giúp được các phụ huynh hiểu hơn về con em cũng như là các bạn học sinh, sinh viên sẽ tìm được cách học phù hợp nhất cho bản thân. Đừng quên thường xuyên ghé thăm website Bamboo School để cập nhật được những kiến thức bổ ích và thông tin mới nhất về các vấn đề liên quan đến học tập nhé!
50+ Cách làm đồ dùng học tập đẹp, cute, đơn giản dễ làm
Sắp đến năm học mới rồi chúng ta hãy cùng nhau học cách làm đồ dùng học tập từ những vật liệu quanh ta như bìa cứng, giấy A4, chai nhựa, ống hút nào. Nhờ những chiếc ống đựng bút, hộp đựng bút, món đồ trang trí để bàn này góc học tập của bạn sẽ xinh xắn hơn. Bạn cũng có thể làm vài món đồ dễ thương để tặng các bạn học trong năm học mới để có thêm nhiều tình bạn đẹp nha.
Cách làm đồ dùng học tập bằng ống hút
Ống hút nhựa là một trong những món đồ tái chế có thể tạo ra rất nhiều món đồ chơi, dùng học tập xinh xắn. Mời các bé cùng Bamboo School bắt tay vào làm ống đựng bút để bàn bằng ống hút nhựa tái chế nha.
Dụng cụ cần chuẩn bị
- Bìa cứng, giấy A4 trắng hoặc giấy A4 màu (tùy thích)
- Ống hút nhựa
- Súng bắn keo
- Keo sữa và cọ quét keo
- Kéo
- Dụng cụ vẽ cơ bản: bút chì, thước kẻ, compa.
Các bước làm ống đựng bút bằng ống hút nhựa
Đây là cách làm đồ dùng học tập bằng ống hút nhựa đơn giản. Hầu hết tất cả các bé trên 6 tuổi đều có thể thực hiện dễ dàng.
Bước 1: Các bé hãy dùng bút chì, compa và thước kẻ để tạo 3 hình lục giác như hình mô tả dưới đây.

Bước 2: Sử dụng súng bắn keo hoặc keo sữa dán ống hút vào phần bìa cứng lục giác như hình bên dưới.

Bước 3: Sau khi ống hút đã dính chặt vào tấm bìa cứng, chúng ta sẽ dùng cọ quét một lớp keo mỏng trên phần bìa cứng.
Sau đó, chúng ta hãy dán tấm giấy trắng che đi phần ống hút như hình bên dưới.

Các bạn hãy dán các mép giấy thừa ra phía sau để phần đế trắng bám chắc hơn nha.

Tiếp theo, chúng ta dùng miếng giấy lục giác còn lại để dán chồng lên phần đế để che đi các mép dán.

Hoàn thành bước 3 chúng ta sẽ được thành phẩm như hình trên.
Bước 4: Chúng ta hãy gấp các ống hút theo cạnh lục giác theo chiều kim đồng hồ, hoặc ngược chiều kim đồng hồ đều được. Nhưng nhất định phải tuân thủ theo một chiều cố định nhé các bạn.

Khi cần nối ống hút, các bạn hãy bóp nhỏ đầu ống hút và xỏ vào một đầu của ống hút tiếp theo.

Bước 5: Khi ống bút đạt đến chiều cao mong muốn, các bạn hãy dùng súng bắn keo để dán các mép ống hút ở vòng cuối cùng. Sau đó cắt bỏ phần ống hút thừa để tạo thành ống đựng bút hoàn chỉnh.

Cách làm đồ dùng học tập bằng lõi giấy vệ sinh
Từ lõi giấy vệ sinh, chúng ta có thể sáng tạo nên nhiều mẫu ống đựng bút xinh xắn. Các bạn hãy tham khảo cách làm dưới đây nhé.
Dụng cụ cần chuẩn bị
- Lõi giấy vệ sinh còn cứng cáp
- Giấy màu theo sở thích
- Đồ trang trí bên ngoài: Dây thừng nhỏ. Các bạn có thể thay thế bằng giấy màu họa tiết.
- Dụng cụ cơ bản: kéo, bút, thước, keo sữa.
Các bước làm ống đựng bút từ lõi giấy vệ sinh
Bước 1: Bạn hãy cắt miếng giấy màu có kích thước vừa bằng với lõi giấy vệ sinh. Sau đó bỏ vào ống lõi giấy. Hoặc bạn có thể sử dụng màu để tô vào trong thành của ruột lõi giấy. Như vậy trông lõi giấy sẽ đẹp hơn.
Bước 2: Quét keo lên xung quanh lõi giấy rồi dán dây thừng nhỏ quấn quanh lõi giấy như hình hướng dẫn bên dưới.

Bước 3: Sau khi quấn dây thừng xong, chúng ta hãy cắt 1 miếng bìa cứng hình tròn dán vào một đầu ống giấy để tạo thành đáy.
Bước 4: Trang trí ống bút theo sở thích. Như vậy là chúng ta đã có một chiếc ống đựng bút để bàn xinh thật là xinh rồi.

Cách làm đồ dùng học tập bằng bìa cắt tông
Nếu nhà bạn có nhiều bìa cắt tông thì hãy tham khảo cách làm kệ đựng đồ dùng học tập để bàn dưới đây nhé.
Dụng cụ cần chuẩn bị
- Bìa cắt tông
- Kéo
- Keo sữa hoặc súng bắn keo.
- Bút, thước.
- Cọ vẽ, màu vẽ
- Giấy màu dán trang trí.
Các bước làm kệ đựng dụng cụ học tập
Bước 1: Bạn hãy xác định vị trí đặt kệ đựng dụng cụ học tập để xác định kích thước kệ phù hợp nhất.
Bước 2: Vẽ ra ý tưởng về chiếc kệ đựng dụng cụ học tập mà bạn thích.
Bước 3: Dùng thước để vẽ nên các hình khối có kích thước chuẩn trên bìa cắt tông.
Bước 4: Cắt ghép các miếng bìa cắt tông thành các hình chữ nhật theo mong muốn.
Bước 5: Dán giấy màu hoặc vẽ họa tiết trang trí lên mỗi chiếc hộp.
Bước 6: Dán các hộp lại thành kệ đựng dụng cụ học tập như kế hoạch ban đầu.
Dưới đây là một số mẫu kệ đựng dụng cụ học tập mà bạn có thể tham khảo:



Cách làm đồ dùng học tập cute
Với những đôi tay khéo léo và sự sáng tạo của mỗi người, chúng ta có thể tạo ra rất nhiều món đồ dùng học tập cute.

Bạn có thể sử dụng những chiếc ly dùng một lần, ly mì tôm tiện dụng để làm hộp đựng bút. Cách làm tương tự như cách làm đồ dùng học tập bằng lõi giấy vệ sinh. Bạn chỉ cần dùng thêm giấy màu, giấy mút, len, bút màu để tạo nên những họa tiết cute như hình mẫu trên. Như vậy là bạn đã có một chiếc ống đựng bút siêu xinh rồi đấy.

Bạn cũng có thể tận dụng những chiếc giày cũ và giấy báo để tạo nên những chiếc ống đựng dụng cụ học tập có một không hai như hình gợi ý trên.
Cách làm đồ dùng học tập bằng giấy A4
Tùy theo loại giấy A4 sẵn có, bạn có thể sử dụng giấy A4 trắng hoặc màu. Sau đó bạn có thể dán giấy hoặc vẽ hình lên các món đồ dùng học tập theo sở thích riêng của mình.

Nhìn hình mẫu hẳn là bạn đã biết cách làm đồ dùng từ giấy A4 rồi phải không. Cách làm khá đơn giản. Bạn chỉ cần dùng giấy màu A4 theo sở thích. Dán thêm một lớp giấy màu A4 để tạo độ cứng cáp cho đồ đựng bút. Sau đó dùng thêm các miếng giấy màu nhỏ để tạo thành chỗ dắt bút, thước và giấy khi chú.

Từ giấy A4 bạn có thể tạo ra nghìn lẻ một chiếc thước kẻ siêu cute như hình mẫu trên. Bạn hãy dán thêm một lớp bìa cứng để giúp cây thước thêm cứng cáp và dùng được lâu hơn nhé.
Cách làm đồ dùng học tập từ đồ tái chế
Từ các món đồ dùng phế liệu thường có trong cuộc sống hằng ngày như chai nhựa, ống hút, lon sữa bò, que kem,… chúng ta có thể sáng tạo nên rất nhiều món đồ dùng học tập để bàn tiện lợi.

Bạn chỉ cần cắt ngang các chai nước ngọt là đã có ngay những chiếc ống đựng dụng cụ học tập rồi. Nếu bạn muốn chúng trông xinh hơn hãy dán hoặc vẽ thêm họa tiết nhé.

Từ chiếc ống thiếc không dùng đến, bạn hãy dán thêm các ống hút nhựa tái chế để tạo thành chiếc hộp đựng bút đa sắc màu.

Nếu bạn là người thích ăn kem, hãy sưu tầm các que kem và dán chúng lại thành kệ đựng bút, khung ảnh như hình trên. Chúng ta vừa có một góc học tập xinh xắn mà chẳng tốn kém. Quan trọng nhất là chúng ta hạn chế lượng rác thải gây ô nhiễm môi trường sống.
Cách làm đồ dùng học tập bằng chai nhựa
Nếu nhà bạn có nhiều chai nhựa với nhiều kích thước khác nhau, bạn hãy tham khảo các mẫu đồ dùng học tập làm từ chai nhựa dưới đây nhé.

Đây là mẫu hộp đựng dụng cụ học tập từ chai nhựa và dây kéo đang được rất nhiều bạn trẻ yêu thích. Tùy theo nhu cầu đựng đồ dùng mà bạn có thể điều chỉnh chiều dài của hộp đựng bút nha.

Xem thêm:
- 40+ cách trang trí vở học sinh đẹp, cute, đẹp nhất, đơn giản dễ làm
- 10 cách tập trung học cao độ hiệu quả, nhanh chóng, không buồn ngủ
- 100+ Ý tưởng vẽ tranh bảo vệ môi trường đẹp nhất, sáng tạo, độc nhất
Cách làm đồ dùng học tập bằng đồ tái chế cực đơn giản và dễ phải không các bạn. Hy vọng với những mẫu cơ bản mà Bamboo School vừa chia sẻ, bạn sẽ tự sáng tạo thêm nhiều món đồ dùng học tập độc đáo khác. Chúc bạn có một góc học tập thật đẹp, thật sáng tạo!
10 cách hết buồn ngủ khi đang học nhanh chóng, đơn giản, hiệu quả nhất
Những ngày thời tiết nắng nóng oi bức thì các bạn học sinh dường như mệt mỏi hơn với bài vở và đặc biệt cơn buồn ngủ bất ngờ ập đến cũng là một trong nguyên nhân khiến các bạn trở nên mất tập trung với việc học. Vậy phải làm thế nào để có thể xua tan được những cơn buồn ngủ luôn chầu chực một bên? Hãy tham khảo những cách đơn giản mà lại hiệu quả nhanh chóng dưới bài viết này nhé!
Tại sao lại dễ buồn ngủ khi học
Để tìm ra cách hết buồn ngủ khi đang học thì đầu tiên chúng ta hãy tìm hiểu nguyên nhân dẫn đến những cơn buồn ngủ không thể chống chọi trước nhé. Theo một số khảo sát thì đa số các bạn học sinh sẽ buồn ngủ vào khoảng 9h sáng và đầu giờ chiều.

Ngoài việc thức khuya để học bài thì vẫn nhiều bạn dành thời gian để lướt web, xem phim… đến rất khuya tầm 1-2h sáng trong khi 7h sáng bạn đã đến trường. Nên cho dù bạn có ngủ đủ 6-8 tiếng nhưng giấc ngủ không sâu thì vẫn luôn buồn ngủ và uể oải.
Đôi khi, môn học nào đó bạn không có hứng thú hay chán ngán không muốn học hoặc cũng có thể do tâm trạng không tốt làm bạn không tập trung vào bài học được cũng là nguyên nhân dẫn đến cơn buồn ngủ. Và việc ngủ gật của học sinh trên lớp đã không còn là chuyện quá xa lạ ngày nay.
12 cách giúp hết buồn khi học bài nhanh chóng hiệu quả
Dưới đây là một số cách hết buồn ngủ khi đang học hiệu quả mà bạn có thể tham khảo.
Thư giãn đôi mắt bị mỏi
Khi bạn phải học quá nhiều dẫn đến việc căng thẳng, mỏi mệt, mắt như tối sầm lại và cơn buồn ngủ ập đến. Thì đó là tín hiệu cho thấy mắt của bạn cần được thư giãn và nghỉ ngơi rồi đấy.
Bạn có thể thư giãn cho mắt bằng cách: đảo mắt nhìn xung quanh, cải thiện thị lực bằng những bài tập về mắt hay giảm mỏi mắt bằng dung dịch chuyên dùng hoặc nhắm mắt trong vài phút.
Lưu ý với cách này khi nhỏ mắt bằng dung dịch nhớ kiểm tra thuốc trước khi nhỏ còn với những bài tập về mắt thì hãy tập thường xuyên và điều độ để đôi mắt khỏe mạnh và chống lại cơn buồn ngủ nhé.
Đi bộ là cách hết buồn ngủ đơn giản nhất
Bạn cố gắng để tỉnh táo nhưng đôi mắt thì luôn muốn sụp xuống để ngủ. Thay vì tiếp tục cố gắng bạn có thể xin ra ngoài đi bộ vài phút, hít thở và lấy lại tinh thần rồi hãy trở lại lớp học.

Và theo một nghiên cứu từ Tiến sĩ Robert Sayer – Giáo sư tại Đại học tại California, Mỹ cho rằng khi chúng ta đi bộ trong 10 phút thì có thể tỉnh táo trong 2 giờ từ việc bơm oxy đến các tĩnh mạch, não và các cơ. Khi cơ thể chuyển động nhẹ nhàng sau một khoảng thời gian ngồi lì thì máu cũng sẽ được tuần hoàn tốt hơn.
Cách tỉnh ngủ: Ăn vặt để tăng năng lượng
Khi lượng đường trong cơ thể hạ thấp cũng là nguyên nhân dẫn đến việc bạn bị mệt mỏi và buồn ngủ. Vậy nên lúc này bạn có thể ăn vặt nhẹ để cung cấp thêm năng lượng.

Bạn có thể chọn một số đồ ăn vặt lành mạnh và có nhiều dinh dưỡng như hoa quả, nước ép, sinh tố hay các loại hạt….Những thực phẩm này sẽ nạp lại lượng đường cho cơ thể và refresh tinh thần hiệu quả đấy.
Nhưng có lưu ý là bạn chỉ nên nạp một lượng vừa phải vì quá nhiều đường nạp vào cơ thể một lúc sẽ khiến bạn uể oải mệt mỏi hơn và tránh sử dụng thức ăn nhẹ dầu mỡ và không lành mạnh nhé.
Cách hết buồn ngủ là uống nhiều nước
Một trong những cách hết buồn ngủ khi đang học hiệu quả là uống nhiều nước. Khi cơ thể mất nước dễ dẫn đến tình trạng mệt mỏi và buồn ngủ. Nên việc bổ sung lượng nước nhiều hơn bình thường là điều cần thiết. Khi lượng nước được nạp vào thì các cơ quan bài tiết sẽ hoạt động tích cực và bạn sẽ đi tiểu nhiều hơn từ đó giúp cơ thể được vận động và thêm tỉnh táo.

Ngoài nước lọc thì bạn cũng có thể sử dụng nước detox hay nước ép từ các loại rau củ quả vừa ngon lại vừa dinh dưỡng như dưa hấu, dâu tây, rau cần tây, cải bó xôi, mận, táo….
Hạn chế sử dụng các loại đồ uống có ga vì nó không bổ sung lượng nước cần thiết cho cơ thể mà còn giảm nhu cầu uống nước làm cơ thể mất nước hơn.
Cách giảm buồn ngủ: Bắt đầu một cuộc trò chuyện
Nếu như cảm thấy không thể nào chiến thắng cơn buồn ngủ bạn có thể nói chuyện một tí với người bên cạnh. Có thể trao đổi về bài học hoặc những câu chuyện khác mang tính giải trí hài hước. Đó là cách hết buồn ngủ khi đang học hiệu quả và còn giảm căng thẳng tốt.

Nếu áp dụng cách này trong lớp bạn lưu ý là không nên trò chuyện quá to để tránh làm ảnh hưởng đến các bạn học khác nhé.
Điều chỉnh ánh sáng mạnh hơn
Môi trường cũng là yếu tố ảnh hưởng đến tâm trạng và tinh thần của bạn. Những nơi có ánh sáng tối, mờ nhạt có thể khiến bạn thêm mệt mỏi và dễ rơi vào tình trạng buồn ngủ hơn. Một số nghiên cứu đã cho rằng việc tiếp xúc với ánh sáng mạnh sẽ làm tăng sự tỉnh táo và giảm sự buồn ngủ. Bạn có thể mở thêm đèn trong lớp học hoặc mở cửa sổ để đón nhận ánh sáng tự nhiên, đảm bảo là sẽ hiệu quả đấy.

Nếu như chỗ ngồi của bạn không thể đón nhận ánh sáng nhiều thì có thể dọn dẹp lại không gian học tập để trông thoáng đãng và sáng sủa hơn. Hoặc bạn cũng có thể sắm thêm một trở thủ đắc lực là chiếc đèn nhoe trên bàn học của mình.
Và lưu ý là bạn chỉ nên điều chỉnh mức ánh sáng phù hợp và đừng quá lạm dụng để có thể bảo vệ đôi mắt luôn sáng và khỏe mạnh.
Chợp mắt khi quá buồn ngủ
Thật sự là đôi khi chúng ta vẫn không thể nào chống chọi lại cơn buồn ngủ ập tới bất ngờ, nên cách hết buồn ngủ khi đang học có thể dùng lúc này chính là chợp mắt một lúc.

Theo bác sĩ Barry Krakow (Mỹ), cơ thể sẽ hoạt động linh hoạt hơn nếu bạn nên có giấc ngủ ngắn tầm 5 – 25 phút. Còn theo Tiến sĩ Allison T. Siebern – Trung tâm Y khoa Giấc ngủ của Đại học Stanford, Mỹ thì cho biết: “Nếu bạn không thể có giấc ngủ ngắn, chỉ cần nhắm mắt và nghỉ ngơi trong 10 phút cũng rất hữu ích”.
Chỉ chợp mắt vài phút nhưng hiệu quả mang lại vô cùng lớn đấy. Nhưng nếu sử dụng cách này bạn hãy đảm bảo là đặt đồng hồ báo thức để không bị ngủ quên hoặc nhờ bạn bên cạnh gọi dậy mà còn tiếp tục học nữa nhé.
Tiếp xúc ánh nắng mặt trời cũng là cách chống buồn ngủ
Không chỉ là cách hết buồn ngủ khi đang học nhanh chóng mà còn để duy trì sự tỉnh táo thì bạn nên tiếp xúc dưới ánh sáng mặt trời mỗi ngày tầm 30 phút. Ngoài ra với những bạn rơi vào tình trạng mất ngủ thì nên tiếp xúc tầm 1 giờ với ánh sáng mặt trời hằng ngày.

Trong trường hợp, bàn học của bạn ngồi gần cửa sổ thì hãy luôn mở cửa để đón nhận không khí tự nhiên và ánh sáng mặt trời như thế sẽ giúp bạn tập trung và thoải mái với việc học hơn.
Lưu ý là khi thời tiết quá nắng nóng, ánh sáng mặt trời quá mạnh làm ảnh hưởng tới thị lực thì bạn nên dùng tới rèm cửa nhưng đừng dùng loại quá dày cản ánh sáng hoàn toàn nhé.
Cách hết buồn ngủ: Tập thể dục đều đặn
Việc vận động cơ thể thường xuyên sẽ giúp lưu thông máu, giãn cơ và sức khỏe tốt. Còn khi bạn vận động trong một thời gian ngắn thì giúp xua tan sự mệt mỏi, uể oải, phục hồi tinh thần cơn buồn ngủ cũng vì vậy mà biến mất. Bạn có thể tham khảo một số động tác thể dục như sau:
- Co giãn các cơ, căng cơ mắt, căng cơ vai và cơ ngực khi quá buồn ngủ.
- Hít thở thật sâu, cố gắng mở mắt to và ngồi thẳng lưng ngay ngắn.
- Dùng tay xoa lên tai theo vòng tròn.
- Ngửa đầu ra sau từ 3-5 lần.

Theo một nghiên cứu với hơn 6.800 người tham gia của các nhà nghiên cứu tại Đại học Georgia (Mỹ) thì phát hiện ra việc tập thể dục giúp giảm mệt mỏi và tiếp thêm năng lượng hơn là dùng thuốc để điều trị về giấc ngủ.
Vậy nên, bạn lưu ý là nên duy trì việc tập thể dục đều đặn hằng ngày tầm 30 phút và tập trước khi đi ngủ tầm 2 – 3 tiếng để không bị khó ngủ và hôm sau không bị ủ rũ, mệt mỏi.
Cách hết buồn ngủ: Điều trị hội chứng ngủ nhiều
Một số người bị mắc hội chứng ngủ li bì (hypersomnia), họ luôn rơi vào tình trạng buồn ngủ liên tục khi đang học hay đang làm việc kể cả lúc giải trí. Và khi mà các phương pháp giúp hết buồn ngủ không hiệu quả thì đó là lúc bạn nên tìm cách điều trị hội chứng này.

Thật chất những người bị mắc hội chứng ngủ nhiều ban ngày thường là do ban đêm bạn rơi vào tình trạng thiếu ngủ hoặc giấc ngủ không ngon, không chất lượng làm cơ thể bạn mệt mỏi và luôn thiếu ngủ vào sáng hôm sau.
Bạn có thể thử thực hiện những cách dưới đây để cải thiện tình trạng này:
- Đảm bảo ngủ đủ giấc: bạn hãy tập thói quen đi ngủ lúc 10h – 11h tối và dậy tầm 5h – 6h sáng để đảm bảo giấc ngủ đủ 7 – 8 tiếng.
- Môi trường xung quanh tạo cảm giác dễ ngủ: lựa chọn chăn gối, mền thoải mái và không gian phòng nên thông thoáng nhất và hạn chế sử dụng thiết bị điện tử từ 1 – 2 tiếng trước khi đi ngủ.
- Tạo thói quen ăn uống đúng giờ giấc: ăn uống lành mạnh đúng bữa sẽ làm bạn ngủ ngon giấc hơn. Không nên sử dụng các đồ uống chứa cồn hay caffeine trước khi ngủ tầm 1 – 2 tiếng.
Xem thêm:
- 100+ cách trang trí bàn học đẹp, gọn gàng, cute, kiểu Hàn Quốc
- 5 cách khoa học để trở nên thông minh hơn bạn nên biết
- Cách chia thời gian học hiệu quả, tối ưu nhất cho học sinh
Tóm lại việc cơn buồn ngủ ập tới khi đang học sẽ gây ảnh hưởng đến kết quả học tập và sức khỏe của bạn. Do đó để tỉnh táo và tập trung tinh thần thì bạn có thể tham khảo những cách hết buồn ngủ khi đang học ở bài viết trên nhé!

