Các trường hợp bằng nhau, đồng dạng của tam giác vuông và ví dụ minh họa có đáp án

Như thế nào là các trường hợp bằng nhau của tam giác vuông, các trường hợp đồng dạng của tam giác vuông? Đó là thắc mắc chung của rất nhiều học sinh khi học Toán. Trong bài viết dưới đây, chúng ta sẽ cùng tìm hiểu cách nhận biết các trường hợp bằng nhau và đồng dạng của tam giác vuông, cũng như giải một số bài tập cụ thể.

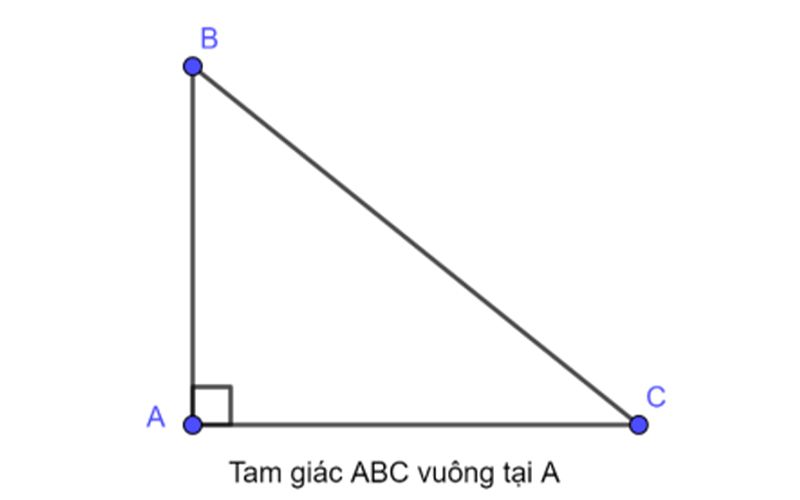
Tam giác vuông là gì? Cách nhận biết tam giác vuông

Hiểu một cách đơn giản, tam giác vuông là tam giác có một góc bằng 90 độ (góc vuông). Các góc vuông này có thể nằm ở 3 đỉnh của một tam giác.

Các cách nhận biết tam giác vuông là:

• Tam giác có một góc vuông là tam giác vuông 
• Tam giác có hai góc nhọn phụ nhau là tam giác vuông 
• Tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia là tam giác vuông 
• Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy là tam giác vuông 
• Tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn là tam giác vuông

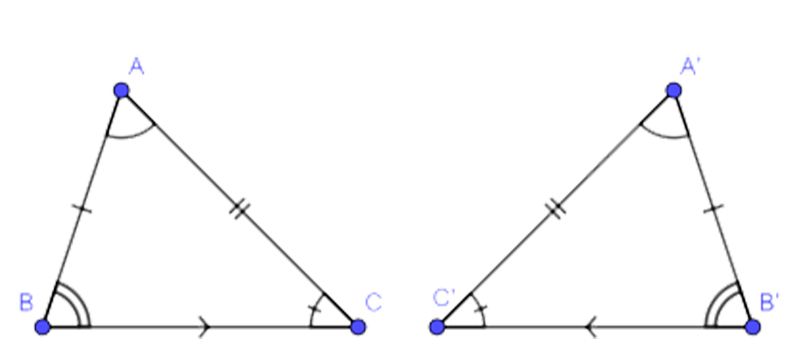
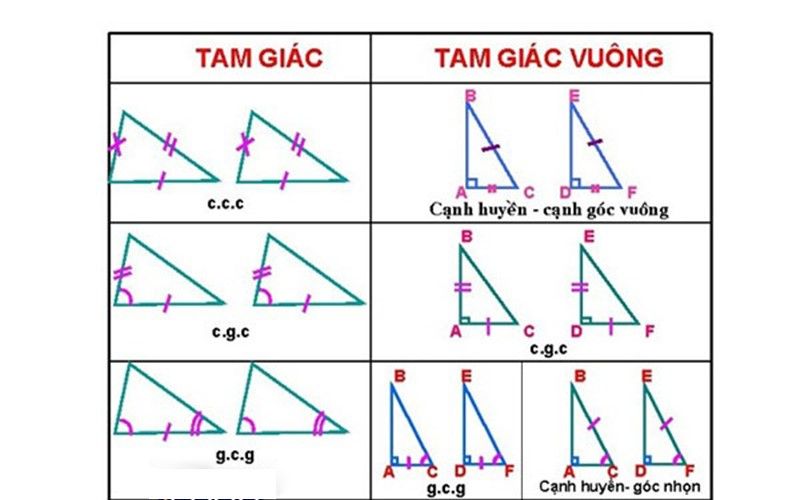
Các trường hợp bằng nhau của tam giác vuông

Các trường hợp bằng nhau của tam giác vuông bao gồm:

• Trường hợp 1: Nếu hai cạnh góc vuông của một tam giác vuông lần lượt bằng hai cạnh góc vuông của tam giác vuông khác, thì tức là hai tam giác vuông đó bằng nhau, theo trường hợp cạnh – góc – cạnh.
• 

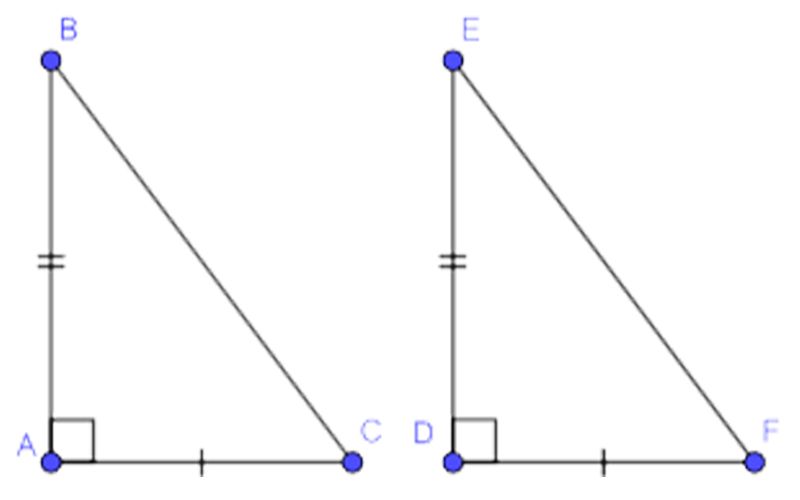
• Trường hợp 2: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này lần lượt bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia, thì hai tam giác vuông đó bằng nhau, theo trường hợp góc – cạnh – góc.

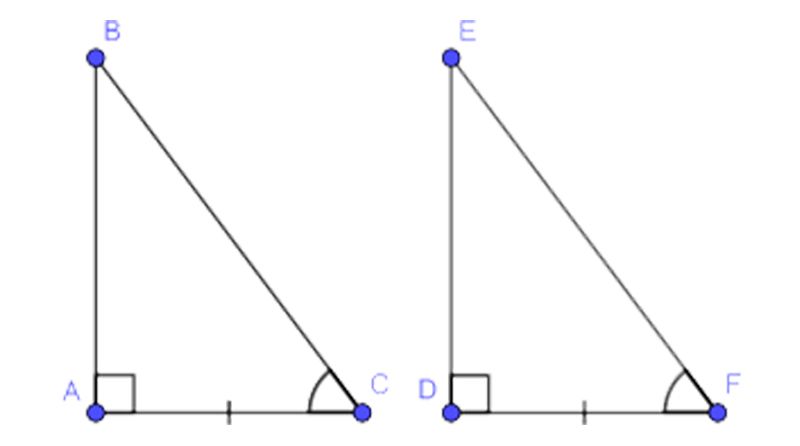
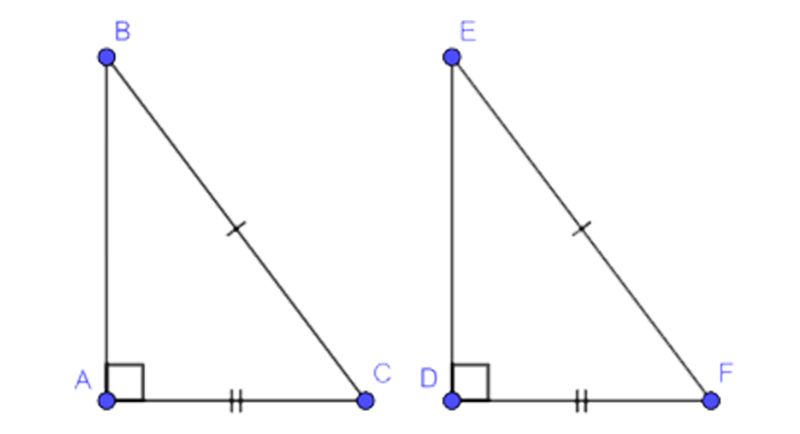
• Trường hợp 3: Nếu cạnh huyền và một góc nhọn của một tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông khác thì hai tam giác vuông đó bằng nhau, theo trường hợp cạnh huyền – góc nhọn. 

• Trường hợp 4: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt bằng cạnh huyền và một cạnh góc vuông của tam giác vuông khác, thì hai tam giác vuông này bằng nhau, theo trường hợp cạnh huyền – cạnh góc vuông.
  

Các trường hợp đồng dạng của tam giác vuông

Để nắm được các trường hợp đồng dạng của tam giác vuông, trước hết ta cần hiểu rõ các trường hợp đồng dạng của một tam giác. Có 3 trường hợp sau đây:

• Trường hợp 1: Các cạnh của một tam giác lần lượt tỉ lệ với các cạnh của tam giác kia thì hai tam giác này đồng dạng, theo trường hợp cạnh – cạnh – cạnh. 
• Trường hợp 2: Nếu hai cạnh của tam giác này lần lượt tỉ lệ với hai cạnh của tam giác kia, và góc tạo bởi hai cạnh đó bằng nhau thì hai tam giác này đồng dạng, theo trường hợp cạnh – góc – cạnh.
• Trường hợp 3: Nếu hai góc của một tam giác có số đo bằng hai góc của tam giác khác thì hai tam giác này đồng dạng, theo trường hợp góc – góc – góc.

Từ đây, ta có thể suy ra các trường hợp đồng dạng của tam giác vuông là:

• Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
• Nếu hai cạnh tạo nên góc vuông của tam giác vuông này tỉ lệ tương ứng với hai cạnh tạo nên góc vuông của tam giác vuông kia thì hai tam giác vuông này đồng dạng với nhau.

Ví dụ bài tập minh họa có đáp án

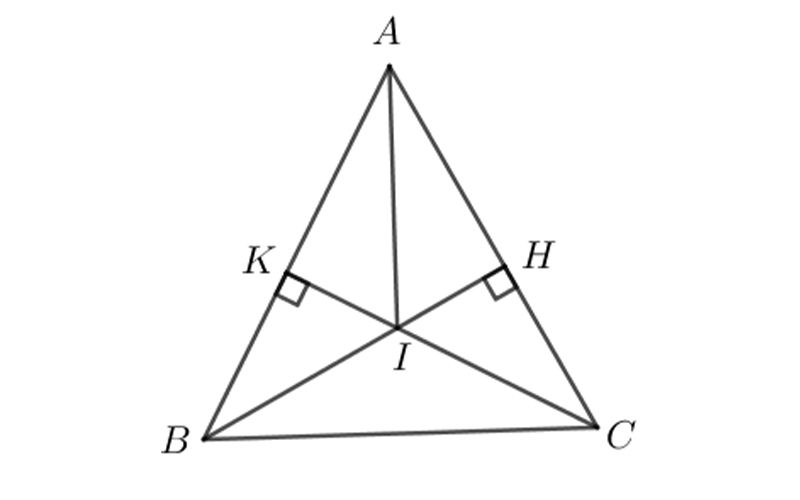
• Bài tập 1: Cho ΔABC cân ở A (∠A < 90 độ). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

1. a) Chứng minh: AH = HK 
2. b) Gọi I là giao điểm của BH và CK. Chứng minh: AI là tia phân giác của góc A

Đáp án:

1. a) Ta có: ΔABC cân tại A (giả thiết) => AB = AC và góc ABC = góc ACB 

Tam giác vuông HAB và KAC có: AB = AC (chứng minh trên), góc A chung 

=> ΔHAB = ΔKAC (cạnh huyền – góc nhọn)

=> AH = AK 

1. b) Tam giác vuông KAI và HAI có: AH = AK, AI là cạnh chung 

=> ΔHAI = ΔKAI (cạnh huyền – cạnh góc vuông) 

=> góc KAI = góc HAI

=> AI là tia phân giác của góc A

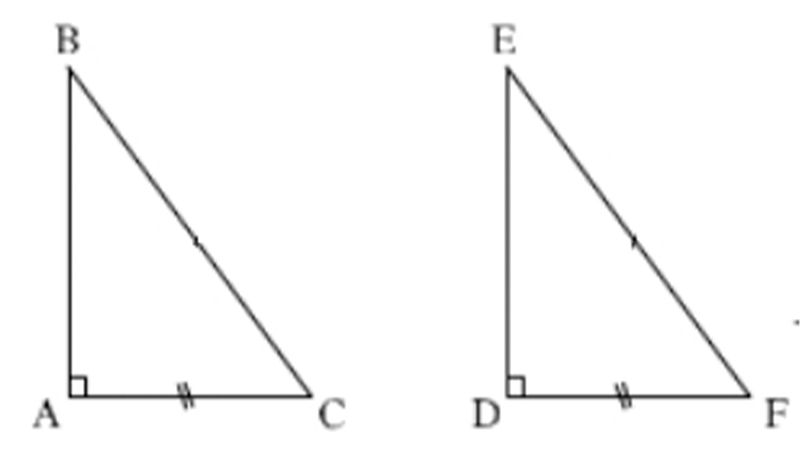
• Bài tập 2: Cho hai tam giác vuông ABC và DEF có góc A = góc D = 90 độ, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF.

Đáp án:

Có thể bổ sung 3 trường hợp sau:

• Trường hợp 1: AB = DE => ΔABC = ΔDEF (cạnh – góc – cạnh) 
• Trường hợp 2: góc C = góc F => ΔABC = ΔDEF (góc – cạnh – góc) 
• Trường hợp 3: BC = EF => ΔABC = ΔDEF (cạnh huyền – cạnh góc vuông)

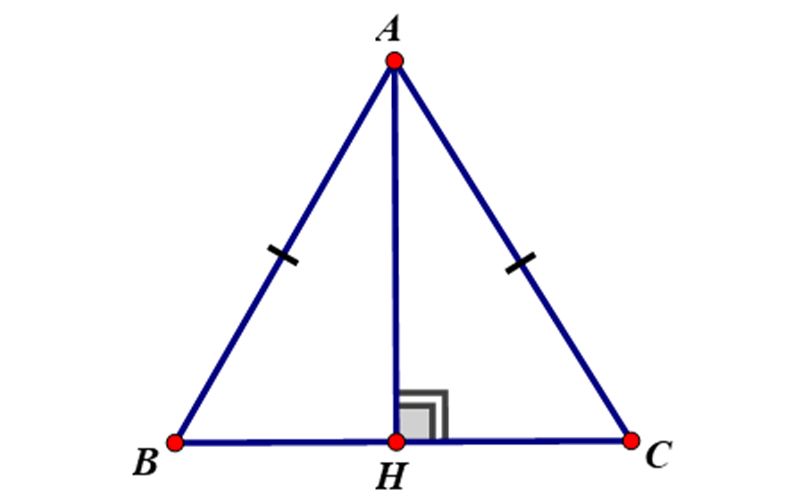
• Bài tập 3: Cho ΔABC cân tại A. AH vuông góc với BC. Chứng minh:

1. a) HB = HC 
2. b) Góc BAH = Góc CAH

Đáp án:

1. a) ΔABH và ΔACH có: AB = AC (giả thiết), AH là cạnh chung 

=> ΔABH = ΔACH (cạnh huyền – cạnh góc vuông) 

=> HB = HC 

1. b) ΔABH = ΔACH (cạnh huyền – cạnh góc vuông) 

=> góc BAH = góc CAH

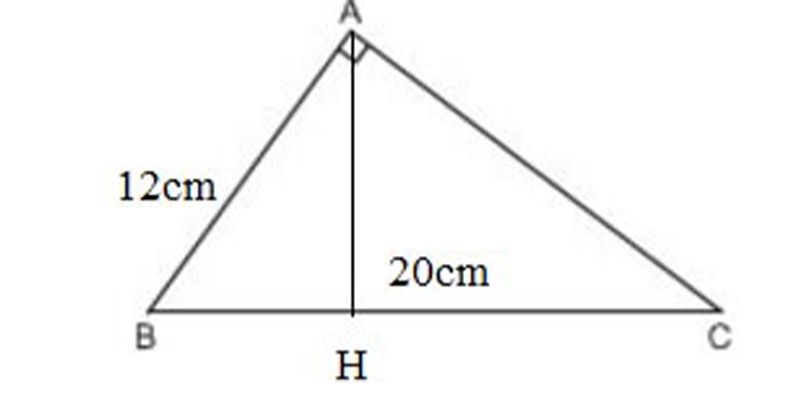
• Bài tập 4: Cho một tam giác vuông  có cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.

Đáp án:

Ta có: Góc B chung

Góc A = góc H = 90 độ

=> ∆ABH ∽ ∆CBA 

=> ABCB = BHBA => AB2 = BH.CB

=> BH = AB2CB = 122/20 = 7,2 (cm)

=> CH = BC – BH = 20 – 7,2 = 12,8 (cm)

• Bài tập 5: Cho hai tam giác đồng dạng với nhau. Trong các phát biểu dưới đây, phát biểu nào sai?

1. Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng. 
2. Tỉ số hai đường phân giác tương ứng bằng tỉ số đồng dạng. 
3. Tỉ số hai đường trung tuyến tương ứng bằng tỉ số đồng dạng. 
4. Tỉ số các chu vi bằng 2 lần tỉ số đồng dạng.

Đáp án: D. Vì trong hai tam giác đồng dạng, tỉ số các chu vi bằng tỉ số đồng dạng.

• Bài tập 6: Cho ΔABC và ΔMNP có góc A = góc M = 90 độ. ABMN = BCNP thì:

1. ΔABC ∼ ΔPMN 
2. ΔABC ∼ ΔNMP 
3. ΔABC ∼ ΔMNP 
4. ΔABC ∼ ΔMPN

Đáp án: C. 

Ta có: Góc A = góc M = 90 độ (giả thiết), ABMN = BCNP 

=> ΔABC ∼ ΔMNP (cạnh – góc – cạnh)\

Xem thêm:

• Cách tính phân tử khối và các dạng bài tập về phân tử khối cơ bản có đáp án
• Công thức tính chu vi hình vuông, chữ nhật, tam giác, hình tròn, hình thoi
• Công thức tính diện tích tam giác, hình thoi, hình vuông, hình chữ nhật, hình tròn

Trên đây là dấu hiệu nhận biết các trường hợp bằng nhau của tam giác vuông và các trường hợp đồng dạng của tam giác vuông. Hy vọng thông qua những ví dụ minh họa ở trên, bạn có thể nắm rõ hơn về các dạng toán này.