Tổng hợp 10 đề thi tiếng Anh lớp 6 giữa học kì 1 2022-2023 có đáp án
Vậy là một mùa thi nữa lại bắt đầu, lần này Bamboo School đã chuẩn bị cho các bạn học sinh lớp 6 tất tần tật về những bộ đề tiếng Anh để hỗ trợ các bạn trong hoạt động ôn luyện sắp tới. Dưới đây là 10 bộ đề thi tiếng Anh lớp 6 giữa học kì 1 năm học 2022 – 2023 (bao gồm đáp án) được tổng hợp một cách chi tiết và bám sát theo đề thi chính thức cho chương trình Trung học Cơ sở. Hy vọng với những bộ đề này, các bạn học sinh sẽ có thể nâng cao trình độ của mình trong quá trình ôn tập và đạt được kết quả thi thật tốt!
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 1
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
Put the verbs in brackets into the correct form
1. Linda (walk)___________ to school every morning.
2. Quan and Lan (learn) _____________ how to use the lawnmower in the garden at the moment.
3. My sister (go) ______________to the supermarket to buy some sugar.
4. Sometimes I (feel) _________________________ really lazy to do anything.
5. Phong and I now (study) _________________________ English in my room.
Read the passage and write True or False.
My name is Nam. There are five people in my family: my father, my mother, my brother, my sister and me. My father is 40 years old. He is a doctor. My mother is 35. She is a teacher. My brother is 16. He is a student. My sister is a student. She is 15 years old. I’m a student too.
1. His father is a teacher.
2. His mother is thirty-five years old.
3. There are four people in his family.
4. His brother is fifteen years old.
5. Nam is a student.
Choose the best answer to complete each of the following sentences.
1. I sometimes ________ to the cinema.
A. go
B. goes
C. going
D. to go
2. John ________much better now.
A. feel
B. feels
C. feeling
D. is feeling
3. I ________football every weekend.
A. study
B. have
C. play
D. do
4. She ________English at the moment.
A. study
B. is studying
C. studies
D. studying
5. She is ________hard for her A levels.
A. having
B. playing
C. studying
D. doing
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 1
Put the verbs in brackets into the correct form
1. Linda (walk)_____Walks______ to school every morning.
2. Quan and Lan (learn) ________Are learning_____ how to use the lawnmower in the garden at the moment.
3. My sister (go) ________Goes______to the supermarket to buy some sugar.
4. Sometimes I (feel) ________feel_____ really lazy to do anything.
5. Phong and I now (study) __________are studying______ English in my room.
Read the passage and write True or False.
1 – False; 2 – True; 3 – False; 4 – False; 5 – True.
Choose the best answer to complete each of the following sentences.
| 1. A | 2. B | 3. C | 4. B | 5.C |
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 2
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
I. Choose the odd one out
1. A. sofa B. chair C. kitchen D. desk
2. A. town house B. villa C. apartment D. school
3. A. funny B. thin C. kind D. lazy
4. A. Literature B. Math C. Draw D. English
5. A. teacher B. mother C. father D. brother
II. Choose the correct answer.
1. In my house, the table is ___________ the sofa and the TV
A. between
B. in
C. next to
D. under
2. Ngoc always helps friends. She is a __________ girl.
A. funny
B. talkative
C. helpful
D. shy
3. My best friend is very ______. She is always nervous and uncomfortable with other people.
A. kind
B. shy
C. funny
D. lovely
4. My brother _____________ to school every day.
A. walks
B. walk
C. waking
D. is walking
5. She has short black______ and big brown eyes
A. mouth
B. hand
C. hair
D. head
III. Read the passage and write True or False.
Hogwarts is a very special school: it is a school for young witches and wizards. It is located near a lake in Scotland, but its students come from Scotland, England, Ireland and Wales. School begins on September 1, and students all get on a special train in London to go to school together. Hogwarts is a boarding school, so students have classes and live at the school. They have to wear robes as their uniform. Each student has an owl for a pet. The owls also carry letters from families. All students play a sport called the quidditch, a kind of flying soccer. Players try to hit the ball with a stick while mounting their flying brooms.
1. Hogwarts is a boarding school.
2. Students go to school by bus.
3. Student wear skirts as uniform.
4. Their pet can carry letters.
5. They play football at school.
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 2
I. Choose the odd one out
1 – C; 2 – D; 3 – B; 4 – C; 5 – A.
II. Choose the correct answer.
1 – A; 2 – C; 3 – B; 4 – A; 5 – C.
III. Read the passage and write True or False.
1 – True; 2 – False; 3 – False; 4 – True; 5 – False.
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 3
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
I. Choose the word which has a different sound in the part underlined.
| 1. | A. kind | B. confident | C. nice | 3. like |
| 2. | A. request | B. project | C. neck | D. exciting |
| 3. | A. foot | B. book | C. food | D. look |
| 4. | A. finger | B. leg | C. neck | D. elbow |
II. Choose the best answer:
1. It’s cold. The students……………warm clothes.
A. wear
B. wears
C. wearing
D. are wearing
2. My friends always do their homework. They’re……………
A. lazy
B. curious
C. hardworking
D. talkative
3. “What would you like to drink now?”-“……………”
A. No, thank you
B. Yes, please
C. I like to do nothing
D. Orange juice, please
4. They are …………… because they do morning exercises every day.
A. fine
B. well
C. healthy
D. healthful
5. Hung often……………his bike to visit his hometown.
A. drives
B. flies
C. rides
D. goes
6. “What are you doing this afternoon?” – “I don’t know, but I’d like to…. swimming.”
A. have
B. do
C. play
D. go
7. Where is the cat? It’s ……..the table and the bookshelf.
A. on
B. behind
C. between
D. under
III. Give the right form of the verbs in brackets:
1. Where’s Tuan? He (do)………….……………………judo in Room 2A now.
2. Mai (take)……………………. …………………………a test next Monday.
3. I usually (skip)…………………………..ropes with my classmates at break time.
4. They (not go)………………………………..to school on Sundays.
IV. Fill in each blank with one suitable from the box to complete the passage
tidying – untidy – bag – on – are – near
Trung’s bedroom is big but messy. There (1)………………..clothes on the floor. There is a big desk (2)…………………the window and there are dirty bowls and chopsticks (3) ……………..……it. He usually puts his school (4) …………………under the desk. His bed is next to the desk and it is also (5)……………………. There is a cap, some CDs and some books on the bed. Trung’s mum is not happy with this, and now Trung is tidying up his room.
V. Read the text and write True (T) or False (F):
Hi. I am Lan. I would like to tell you about my new school. It is in a quiet place not far from the city center. It has three buildings and a large yard. This year there are 26 classes with more than 1.000 students in my school. Most students are hard-working and serious. The school has about 40 teachers. They are all helpful and friendly. My school has different clubs: Dance, English, Arts, Football and Basketball. I like English, so I joined the English club. I love my school because it is a good school.
1. Lan’s new school is in a noisy place near the city center.
2. Lan’s school has three buildings and twenty classes.
3. The teachers are helpful and friendly
4. There are five clubs in Lan’s new school.
5. Lan doesn’t like English.
VI. Rearrange the words to make a meaningful sentence:
1. can/ turn on/ the/ please/ lights/ you/?
__________________________________________________________
2. you/ would/ have/ a picnic/ to/ like/ next Sunday/?
__________________________________________________________
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 3
I. Choose the word which has a different sound in the part underlined.
1 – B; 2 – D; 3 – C; 4 – A.
II. Choose the best answer:
1 – D; 2 – C; 3 – D; 4 – C; 5 – C; 6 – D; 7 – C.
III. Give the right form of the verbs in brackets:
1 – is doing; 2 – is taking; 3 – skip; 4 – don’t go.
IV. Fill in each blank with one suitable from the box to complete the passage
1 – are; 2 – near; 3 – on; 4 – bag; 5 – untidy.
V. Read the text and write True (T) or False (F):
1. F
2. F
3. T
4. T
5. F
VI. Rearrange the words to make a meaningful sentence:
1. Can you please turn on the lights?
2. Would you like to have a picnic next Sunday?
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 4
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
I. LANGUAGE FOCUS (2,5 ps)
Choose the word with a different way of pronunciation in the underlined part.
| 1. | A. vases | B. dishes | C. tables |
| 2. | A. books | B. keys | C. pots |
| 3. | A. study | B. uniform | C. Monday |
Choose the best option to complete each sentence. Circle A, B or C.
1. There ___________ two pictures and a clock on the wall.
- is
- are
- be
2. He _____________ his grandparents next weekend?
- is visiting
- visit
- Is he visiting
3. We always cook meals in the ___________.
- kitchen
- bedroom
- living room
4. In Mi’s house the tea table is in the middle of the living room. In my house, it is ___________ the sofa and the armchair.
- between
- in
- next to
5. Ngoc talks a lot. She is a __________ girl.
- funny
- talkative
- cheerful
6. My best friend is very ______. She cares about other people.
- kind
- shy
- funny
7. My father _____________ to work by bus every day.
- goes
- go
- going
II. WRITING (2,5 ps)
Rearrange the sentences. You can not change the words.
| Example: 0. There/ library/ many/ the/ books/ are/ in/.
=> There are many books in the library. |
- They/ are/ on/ playground/ playing/ the/ games/ . / .
_________________________________________________________
- The/ are/ now/ students/ playing/ .
_________________________________________________________
- Does/ drive/ your/ you/ mother/ to school/ ?
_________________________________________________________
- What/ you/ are/ at/ looking/ ?
_________________________________________________________
- I/ Tuesdays/ on/ English/ study
_________________________________________________________
III. READING (2,5 ps)
Read the passage written by Mai. Decide whether the sentences are true (T) or false (F). Circle T or F.
I have many good classmates, but my best friends are Vy and Thảo. Vy sits next to me, and Thảo sits in front of us. Both of them are very smart and creative. Vy is good at English, and Thảo is best at maths. They help me a lot with my study. During break time, we often play many games together. Our favorite is hide and seek. Thảo and I like science, so we join the school’s science club. Vy likes dancing, so she is in the dance club. Vy often performs in front of the whole school at the beginning of each month, and we love watching her. I think I’m very lucky to have two best friends!
| 1. | Mai is mainly talking about her school activities. | T | F |
| 2. | Mai, Vy and Thảo sit at the same table. | T | F |
| 3. | They don’t have any favorite game. | T | F |
| 4. | Mai’s friends help her to study. | T | F |
| 5. | Vy is not in the same club as Mai and Thảo. | T | F |
IV. LISTENING (2,5 ps)
Listen to a girl talking about a person. Circle the best answer A, B or C.
| 1. | Who is the author talking about? | ||
| A. Her friends | B. Her neighbor | C. Her best friend | |
| 2. | Which of these sentences describes Mai? | ||
| A. Mai is short with long straight hair and a round face. | |||
| B. Mai is tall with short straight hair and a long face. | |||
| C. Mai is tall with long straight hair and a round face. | |||
| 3. | Which clothing does Mai like wearing? | ||
| A. T-shirts and skirts | B. T-shirts and jeans | C. Skirts and dresses | |
| 4. | Which of the signs is Mai’s sign? | ||
| A. Virgo | B. Libra | C. Pisces | |
| 5. | Why does the author like Mai? | ||
| A. Because she’s interesting. | B. Because she’s friendly. | C. Because she’s talkative. | |
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 4
I. Language focus.
1. Pronunciation
1- C. Tables 2- B. Keys 3- B. uniform
2. Vocabulary and grammar
4- B. Are 5- C. Is he visiting 6- A. kitchen
7- A. between 8- B. Talkative 9- A. kind 10- A. goes
II. Writing
1- They are playing games on the playground.
2- The students are playing now.
3- Does your mother drive you to school?
4- What are you looking at?
5- I study English on Tuesday.
III. Reading
1 – F 2 – F 3 – F 4 – T 5 – T
IV. Listening
1 – C 2 – C 3 – B 4 – B 5 – A
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 5
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
I. Find the word which has a different sound in the part underlined.
| 1. A. pastime | B. winter | C. ice | D. bike |
| 2. A. sandwich | B. chair | C. school | D. chicken |
| 3. A. lamp | B. play | C. stay | D. crazy |
| 4. A. couches | B. boxes | C. houses | D. tables |
II. Choose the correct answer A, B, C, or D to finish the sentences.
5. – “_________________class are you in?” – “Class 6B.”
A. Which
B. Where
C. When
D. Whose
6. In many schools in Vietnam students have to wear a _________________. .
A. clothing
B. suit
C. uniform
D. coat
7. My father likes _________________ up early and watering the flowers in our garden.
A. going
B. staying
C. getting
D. get
8. What do you usually_________________ for breakfast?
A. to have
B. have
C. having
D. has
9. My friend, Nga is very hard-working. She _______most of her time studying.
A. to spend
B. spends
C. spending
D. spent
10. This Saturday we_________________to the Art Museum.
A. go
B. is going
C. are going
D. went
III. Put the verbs in brackets in the present simple tense or present continuous tense.
11. Phong often (play) _____________football on the weekend.
12. We (visit) _____________our grandparents this weekend.
13. They (not go) _____________to work on Saturdays and Sundays.
14. Mr. Ninh (not work) _____________in the office every Friday afternoon.
15. Mary (have) _____________short hair?
IV. Underline the correct answer to complete sentences
16. What (is there/there is) opposite your house?
17. Our store is (next/next to) the photocopy store.
18. The police station is between the drugstore (or/and) the bookstore.
19. Is her school (in front of/ of front in) the park.
20. There (is/are) a restaurant and two hotels on our street
V. Choose the letter A, B, C, or D that needs correcting
21. She get up at 6:30 every day.
A. She
B. get up
C. at 6:30
D. every day
22. She plays sports in afternoon.
A. She
B. plays
C. sports
D. in afternoon
23. Every evening, she do her homework.
A. Every evening
B. she
C. do her
D. homework
24. There are trees and flowers on the park.
A. are
B. trees
C. flowers
D. on
25. What color are her hair? It is red.
A. What
B. are
C. is
D. red
VI. Read the following passage, then choose the correct answer A, B, C or D.
Jack is my best friend. He is a teacher. He’s teaching in a school in London. Every morning he gets up at about 7 o’clock, has breakfast and a cup of coffee. Then he leaves for work. The school is far from his home, so he can’t walk there. He must go by bus. He has lunch at a restaurant nearby. In the afternoon he works until 5 or 5:30 and then he goes home. He doesn’t work on Saturdays or Sundays. He goes to the cinema or theatre. He is married and he has a son. He loves his family. They are very happy.
26. What’s Jack’s job?
A. a student
B. a teacher
C. a writer
D. a doctor
27. What does “leave for” means?
A. run to
B. swim to
C. fly to
D. go to
28. What’s his favorite drink?
A. milk
B. tea
C. coffee
D. lemonade
29. According to the passage, which of the following statements is not true ?
A. He doesn’t have lunch at home.
C. He doesn’t have any son.
B. He works in a school.
D. He goes to work by bus.
VII. Make sentences using the words and phrases given.
30. Mai and Lan / my / new / friends.
=> …………………………………………………………………………………………………………………………
31. They / 11 years old / and / they / be / class / 6A.
=> ………………………………………………………………………………………………………………………….
32. They / live / Hai Ba Trung Street.
=> ………………………………………………………………………………………………………………………..
VIII. Use the words given and other words, complete the second sentence so that it has a similar meaning to the first sentence. Do not change the word given. (Use 2-5 words in total).
33. The lamp is behind the computer. of
=> The computer………………………………………………………………..the lamp.
34. There is an air conditioner and a ceiling fan in our living room. has
=> Our living room…………………………………………………………………ceiling fan.
35. My favourite room in the house is the living room. best
=> I like ……………………………………………………………………………… in the house.
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 5
1 – B; 2 – C; 3 – A; 4 – D.
5 – A; 6 – C; 7 – C; 8 – B; 9 – B; 10 – C.
11. plays; 12. are living; 13. don’t go.
14. doesn’t work; 15. Does … have.
16. is there; 17. next to; 18. and; 19. in front of; 20. is.
21 – B; 22 – D; 23 – C; 24 – D; 25 – C.
26 – B; 27 – D; 28 – C; 29 – C.
30. Mai and Lan are my new friends.
31. They are 11 years old and they are in class 6A.
32. They live on Hai Ba Trung Street.
33. The computer is in front of the lamp.
34. Our living room has an air conditioner and ceiling fan.
35. I like the living room best in the house.
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 6
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
I. Find the word which has a different sound in the part underlined.
| 1. A. hot | B. wardrobe | C. poem | D. rosy |
| 2. A. houses | B. toothbrushes | C. stores | D. glasses |
| 3. A. oven | B. brother | C. stove | D. roses |
II. Find the word which the stress pattern pronounced differently from others.
| 4. A. teacher | B. student | C. lecture | D. engineer |
| 5. A. diploma | B. folder | C. backpack | D. sharpener |
III. Complete the sentences with the present simple or present continuous form.
- We (visit) ………………. our grandparents now.
- They (not go) ………………. to work on Saturdays and Sundays.
- Mr. Ninh (not work) ………………in the office at the moment.
- ………………. Mary (have) …………….. short hair?
- I (meet) ………………. my uncle and aunt every day.
IV. Choose the best option (A, B, c or D) to complete these sentences.
11. John ………………. in a house in the countryside.
- live
- lives
- living
- to live
12. We might ………….. smart phones surfed the Internet.
A. have
B. having
C. to have
D. had
13. Robot will help us do the housework such as cleaning the floor, ……….meals and soon.
A. cooking
B. to cook
C. go
D. going
14. If we ………………. waste paper, we will save a lot of trees.
A. repeat
B. recycle
C. review
D. remark
15. If we plant more trees in the school yard, the school will be a ………………. place.
A. darker
B. dirtier
C. greener
D. more polluted
16. ……………….your house have an attic? – ………………., it does.
A. Do/ Yes
B. Do/No
C. Does/Yes
D. Does/No
17. Where are you, Hai? – I’m downstairs. I ………………… to music.
A. listen
B. to listen
C. am listening
D. listening
18. My close friend is ready ………………. things with her classmates.
A. share
B. to share
C. shares
D. sharing
19. On Saturday, we ………………….to the Art Museum.
A. go
B. going
C. is going
D. are going
20. My best friend, Hanh,is ………………. She talks all the time.
A. talkative
B. kind
C. confident
D. creative
V. Read the email, choose the best answer A, B, c or D and write.
From: an@fastmail.com
To: nick@fastmail.com
Subject: My best friend
Hi Nick,
It’s great to hear from you. I want to tell you about my best friend.
My grandma is my best friend. She’s 68 years old. She lives with our family. She was a Maths teacher at a secondary school. She likes getting up early and watering the flowers in our garden, she usually helps me with my homework. In the evening, she tells me interesting stories. She also listens to me when I’m sad, which makes me love her the most.
I love my grandma very much. What about you? Who’s your best friend?
Please write to me soon.
Bye bye,
21. The e-mail is about ……………………………………
A. An’s best friend at school
B. An’s grandma
C. An’s math teacher
D. An’s mom
22. …………………………………… is his grandma’s hobby.
A. helping An do his homework
B. watering flowers
C. telling stories
D. listen to music
23. An usually listens to his grandma’s stories in the …………………………………
A. morning
B. afternoon
C. evening
D. at noon
24. An likes his grandma best because ……………………………………
A. she lives with his family.
B. she gets up early every morning,
C. she always listens to him when he’s sad.
D. she is a Maths teacher.
VI. Reorder the following words to make meaningful sentences.
25. a/ classroom/ map/ and/ has/ My/ a/ projector/.
…………………………………………………………………………………………………………………………
26. Sue/ going/ school/ is/ to/ by / tomorrow/ bus.
…………………………………………………………………………………………………………………………
27. The/ in/ bookshelf/ room/ is/ my/ next/ the/ to/ window.
…………………………………………………………………………………………………………………………
28. difficult/ friends are talking/ My/ about/ a/ exercise/ now.
…………………………………………………………………………………………………………………………
29. Lien/ house/ is/ live/ My/ and/ classmate/ near/ I/ her/ too.
…………………………………………………………………………………………………………………………
30. some/ are/ school/ front/ trees/ in/ my/./ There/ of/
………………………………………………………………………………………………………………………
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 6
1 – A; 2 – C; 3 – B; 4 – D; 5 – A.
6 – are visiting; 7 – don’t go; 8 – isn’t working; 9 – Does – have; 10 – mee.
11 – B; 12 – A; 13 – A; 14 – B; 15 – C.
16 – C; 17 – C; 18 – B; 19 – A; 20 – A.
21 – B; 22 – B; 23 – C; 24 – C.
25. My classroom has a map and a projector.
26. Sue is going to school by bus tomorrow.
27. The window is next to the bookshelf in my room.
28. My friends are talking about a difficult exercise now.
29. My classmate is Lien and I live near her house too.
30. There are some trees in front of my school.
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 7
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
Chọn đáp án đúng trong số A , B, C , D để hoàn thành câu
1. I ____________________ the Ngoc Son Temple tomorrow.
- is going to visit
- am visiting
- am going to visit
- visit
2. It’s usually cold in the ____________.
- winter
- spring
- summer
- fall
3. ____________ are you going to stay? _ In a hotel.
- What
- Where
- When
- How long
4. How often does Phong watch television?
- Twice a day
- For two days
- On Sundays
- A day twice
5. What are they doing now?
- They are going to watch a soccer match.
- They watch a soccer match.
- They are watching a soccer match.
- They watching a soccer match.
6. Does Thu usually go swimming ___________ the summer?
- on
- in
- for
- on
7. ____________ are they going to stay in Da Lat? _ For a week.
- How long
- What
- How often
- Where
8. My father sometimes ____________ to music.
- is going to listen
- is listening
- listens
- listen
9. Let ‘s _____________ to the movies.
- going
- go
- to go
- to going
Đọc kỹ đoạn văn sau đây và trả lời các câu hỏi
Mrs. Chi is working in the garden. She has a beautiful garden behind her house. There are a lot of flowers in the garden all year round. She usually puts flowers in the living room. She has many friends in Qui Nhon. Her friends are going to visit her family next week. Mrs. Chi often gives them a few flowers when they leave her house.
- What is Mrs Chi’s Garden like?
…………………………………………………………………………………….
- Are there always many flowers in her garden?
……………………………………………………………………………………
- Where does she usually put flowers?
…………………………………………………………………………………….
- When are her friends going to visit her family?
……………………………………………………………………………………
- What does she often give them when they leave her house?
……………………………………………………………………………..
Đặt câu hỏi cho từ gạch chân
- They are going to stay in Nha Trang for two days.
……………………………………………………………………………….
- Nam plays badminton twice a week.
………………………………………………………………………………….
- Thu is watching television now.
……………………………………………………………………………………
Dùng từ gợi ý viết thành câu hoàn chỉnh
- It / often warm / the spring.
……………………………………………………………………………
- What / you / go / do / tomorrow morning?
………………………………………………………………………………
- What about / stay / Hue / a week?
…………………………………………………………………………………
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 7
Chọn đáp án đúng trong số A , B, C , D để hoàn thành câu
1 – C; 2 – A; 3 – B; 4 – A; 5 – C.
6 – B; 7 – A; 8 – C; 9 – B.
Đọc kỹ đoạn văn sau đây và trả lời các câu hỏi
1 – It is a beautiful garden.
2 – Yes, there are.
3 – She puts them in the living room.
4 – Next week.
5 – She gives them a few flowers.
Đặt câu hỏi cho từ gạch chân
1 – How long are they going to stay in Nha Trang?
2 – How often does Nam play badminton?
3 – What is Thu doing now?
Dùng từ gợi ý viết thành câu hoàn chỉnh
1 – It is often warm in the spring.
2 – What are you going to do tomorrow morning?
3 – What about staying in Hue for a week?
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 8
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
Hãy chọn một đáp án đúng nhất
1. How many ……………………. are there?
- book
- books
- a book
- the book
2. They are in their ………….. room.
- living
- to live
- live
- to live
3. Thu: What’s her name? – Lan: ……………………
- His name’s Hoa
- My name’s Hoa
- Your name’s Hoa
- Her name’s Hoa
4. He is ……………
- doctors
- teachers
- an engineer
- students
5. Twenty – two + thirty-seven = ………………………
- Fifty- six
- Fifty-nine
- Fifty- seven
- Fifty- eight
6. A: Are they twelve ? – B:………….
- Yes, he is
- No, he isn’t
- No, they aren’t
- Yes, we are
7. I live…………. Can Tho city.
- on
- in
- at
- with
8. A: …………. are you? – B: I’m fine, thanks.
- What
- Where
- Who
- How
9. A: How old are you?
- He’s eleven
- I’m fine
- I’m eleven years old
- She’s eleven years old
10. Miss Hoa: Goodmorning, class. – Children: …………………….
- Good afternoon, teacher
- Good evening, teacher
- Hi, teacher
- Good morning, teacher
Đọc đoạn văn .Sau đó trả lời câu hỏi
My name’s Ba. I’m a student. This is my family. There are four people in my family: my father, my mother, my sister and me. My father is fifty years old. He’s a doctor. My mother is forty-six. She’s a nurse. My sister is a student.
Câu hỏi :
- What’s his name?
…………………………………………………………………
- How old is his father?
…………………………………………………………………
- How old is his mother?
…………………………………………………………………..
- What does she do?
…………………………………………………………………….
Chia động từ trong ngoặc vào hình thức đúng
- Mr. Tan and Miss Lien (be) ……………..teachers.
- I (live) ………………….. in Ha Noi.
- That (be) …………………….. my classroom.
- I (be) ……………….. a student.
Tìm lỗi sai và sửa.
- My school is in the city. They is big.
- We have English at Monday and Friday.
- My mother often get up at 6.00 o’clock in the morning.
- What does Mr. Minh travel to work?
- I’m hungry. I’d like some chicken and some rices.
- What are you going do on the weekend?
- The Nile River is the longer river in the world.
- We are burning too many coal, oil and gas.
- She cooks in the kitchen now .
- We have lots of beautiful beach.
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 8
Hãy chọn một đáp án đúng nhất
1 – B; 2 – A; 3 – D; 4 – C; 5 – B;
6 – C; 7 – B; 8 – D; 9 – C; 10 – D;
Đọc đoạn văn .Sau đó trả lời câu hỏi
1 – His name is Ba.
2 – He is fifty years old.
3 – She is forty – six years old.
4 – She is a nurse.
Chia động từ trong ngoặc vào hình thức đúng
1 – are; 2 – live; 3 – is; 4 – am;
Tìm lỗi sai và sửa.
1 – They thành It;
2 – at thành on;
3 – get thành gets;
4 – What thành How;
5 – rices thành rice;
6 – do thành to do;
7 – longer thành longest;
8 – many thành much;
9 – cooks thành is cooking;
10 – beach thành beaches;
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 9
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
Choose the best answer.
1. Find the word which has a different sound in the part underlined.
A. trees
B. breads
C. bears
D. lips
2. My friends never do their homework. They’re……………
A. hardworking
B. curious
C. lazy
D. talkative
3. “What would you like to eat now?”-“ ……………”
A. No, thank you
B. Yes, please
C. I like to do nothing
D. Beef noodles, please
4. They …………… food because they are hungry.
A. don’t eat
B. drink
C. eat
D. don’t drink
5. Phong often……………on foot to visit his grandma.
A. drives
B. flies
C. goes
D. rides
6. “What are you doing this afternoon?” –“I don’t know, but I’d like to…..the football.”
A. have
B. do
C. go
D. play
7. Where is the pencil? It’s ……..the pencil and notebook.
A. on
B. behind
C. between
D. under
8. It’s rainy. The students……………raincoat.
A. wear
B. wears
C. wearing
D. are wearing
Give the right form of the verbs in brackets
1. Where’s Lan? She (do)………….…………………… aerobics in the gym now.
2. Linh (take)……………………………………………….an exam next Tuesday.
3. I usually (skip)…………………………..ropes with my classmates at break time.
4. They (not go)………………………………..to school at the weekends.
Fill in each blank with one suitable from the box to complete the passage.
tidying – untidy – bag – on – are – near
Trung’s bedroom is big but messy. There (1) ………………..clothes on the floor. There is a big desk (2) …………………the window and there are dirty bowls and chopsticks (3) ……………… it. He usually puts his school (4)…………………under the desk. His bed is next to the desk and it is also (5)……………………. There is a cap, some CDs and some books on the bed. Trung’s mum is not happy with this, and now Trung is tidying up his room.
Read the text and answer the question.
Hi. I am Lan. I would like to tell you about my new school. It is in a quiet place not far from the city center. It has three buildings and a large yard. This year there are 26 classes with more than 1.000 students in my school. Most students are hard-working and serious. The school has about 40 teachers. They are all helpful and friendly. My school has different clubs: Dance, English, Arts, Football and Basketball. I like English, so I joined the English club. I love my school because it is a good school.
1. Where is Lan’s school?
2. How many classes are there in her school?
3. How are the teachers in Lan’s school?
4. What subjects does Lan like?
5. Does Lan’s school have different clubs?
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 9
Choose the best answer.
1 – D; 2 – C; 3 – D; 4 – C; 5 – C; 6 – D; 7 – C; 8 – D.
Give the right form of the verbs in brackets
1 – is doing; 2 – will take; 3 – skip; 4 – don’t go.
Fill in each blank with one suitable from the box to complete the passage.
1 – are; 2 – near; 3 – on; 4 – bag; 5 – untidy.
Read the text and answer the question.
1 – It is far from the city center.
2 – There are 26 classes.
3 – They are all helpful and friendly.
4 – She likes English.
5 – Yes, it does.
Đề thi tiếng Anh lớp 6 giữa học kì 1 số 10
Đề thi tiếng Anh 6 giữa Học kì 1
Thời gian làm bài: 45 phút
Find the word that has different sound from the others by circling A, B, C or D.
| 1. A. camp | B. vocabulary | C. villa | D. band |
| 2. A. arms | B. ears | C. eyes | D. lips |
| 3. A. kitchen | B. choir | C. children | D. chair |
| 4. A. oranges | B. places | C. faces | D. lakes |
| 5. A. study | B. club | C. uniform | D. funny |
Choose the correct answer to complete each sentence by circling A, B, C or D.
1. Which word is different from the others?
A. rubber
B. ruler
C. compass
D. bicycle
2. They are healthy. They do…………………every day.
A. football
B. physics
C. judo
D. breakfast
3. Look! They boys…………football in the schoolyard.
A. playing
B. is playing
C. are playing
D. play
4. My sister……………….TV every night.
A. watch
B. watches
C. watching
D. is watching
5. My friends want to study in a/an………………………. school because they want to learn English with English speaking teachers there.
A. national
B. international
C. creative
D. boarding
6. Are there three………………in the living room?
A. lamp
B. lamps
C. a lamp
D.an lamp
7. The sink is next……. the fridge.
A.to
B. on
C. in
D. between
8. We live in the mountainous area and we live in a………………. house
A. villa
B. town
C. stilt
D. apartment
9. Mai and Lan……………… a picnic tomorrow.
A. have
B. has
C. having
D. are having
10. Odd one out:
A. sofa
B. attic
C. bathroom
D. kitchen
Put the verbs in the right forms.
- They (do) ___ their school project now.
- Listen! My students (play) _____the piano in the music room.
- My mother always (tell) _____me stories before I go to bed.
- It (not, rain) _____________________ at present.
- 5.My father (not, go) ______to work by car every day.
- Quynh (have) _______ Maths, English on Mondays?
Read the passage then answer the questions below.
Hi! I am Vinh. I come from Da Nang, Viet Nam. I like English and I go to English club everyday. My friends like English, too. It is very interesting to learn English. My English teacher is great and funny. She always makes our English lessons new and different. A lot of tourists come to Da Nang every year, so we have more chances to practice our English. This Saturday I am going to Han River with my parents to watch the international firework competition. I hope I am meeting many English people there.
1. Which subject does Vinh like?
…………………………………………………………………………………………………
2. Is it interesting to learn English?
…………………………………………………………………………………………………
3. Where is Vinh going to this Saturday?
…………………………………………………………………………………………………
Read the passage then choose the right answer to complete each blank.
Da Lat is nice. It’s cool all year round! There (1)……… a lot of things to see and lots of tourists, too. There are ten rooms in the Crazy House hotel. They are named (2)…………. different animals. There is a Kangaroo room, an Eagle room, and even an Ant room. I am staying in the Tiger room. It’s called the Tiger room (3)…………there is a big tiger on the wall.
The Tiger room is (4)………….the bathroom door and the window. The bed is under the window- but the window is a strange shape. I put my books (5)…….. the shelf. There is a lamp, a wardobe (6)………. a desk. There are clothes on the floor – it’s messy, just like my bedroom at home.
| 1. A. is | B. are | C. am | D. is not |
| 2. A. after | B. at | C. on | D. in |
| 3. A. but | B. and | C. because | D. with |
| 4. A. next to | B. between | C. behind | D. under |
| 5. A. on | B. in | C. after | D. with |
| 6. A. call | B. and | C. with | D. near |
Đáp án tiếng Anh lớp 6 giữa học kì 1 số 10
Find the word that has different sound from the others by circling A, B, C or D.
1 – C; 2 – D; 3 – B; 4 – D; 5 – C.
Choose the correct answer to complete each sentence by circling A, B, C or D.
1 – D; 2 – C; 3 – C; 4 – B; 5 – B.
6 – B; 7 – A; 8 – C; 9 – D; 10 – A.
Put the verbs in the right forms.
1 – are doing; 2 – are playing; 3 – tells.
4 – is not raining; 5 – doesn’t go; 6 – Does Quynh have.
Read the passage then answer the questions below.
1 – He likes English.
2 – Yes, it is.
3 – He is going to Han river with his parents.
Read the passage then choose the right answer to complete each blank.
1 – B; 2 – A; 3 – C; 4 – B; 5 – A; 6 – B.
Tải bộ đề thi tiếng Anh lớp 6 giữa học kì 1
[su_button url=”https://docs.google.com/document/d/1qUIfn2HrPZxa6fISffxKCyPc7ysW1awXGzDdeMkZ9Kg/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 MÔN TIẾNG ANH LỚP 6[/su_button]
Xem thêm:
- Tổng hợp đề thi ngữ văn lớp 6 giữa kì 1 chương trình mới có đáp án
- Tổng hợp 7 đề thi tiếng Anh lớp 7 giữa học kì 1 chương trình mới có đáp án
- Tổng hợp 4 bộ đề thi giữa kì 1 văn 8 2022-2023 có đáp án (Tải nhiều nhất)
Bên trên là tổng hợp 10 đề tiếng Anh kiểm tra giữa học kì học của khối lớp 6. Với bộ đề này, Bamboo School hy vọng các bạn có một kì thi thật thành công và sẽ có những buổi ôn tập hiệu quả đạt kết quả kiểm tra thật tốt!
Thế năng là gì? Công thức tính thế năng trọng trường và đàn hồi
Một trong những kiến thức chủ chốt của chương trình Vật lý lớp 10 nói riêng và cấp bậc trung học phổ thông nói chung đó chính là về thế năng. Không chỉ là kiến thức trên sách vở mà thế năng còn gắn liền với thực tiễn đời sống. Thế nhưng khái niệm thế năng là gì? Những loại thế năng sẽ gặp trong chương trình học cùng các công thức mà các em học sinh cần nhớ. Tất cà sẽ được gói gọn trong bài viết “Thế năng là gì? Công thức tính thế năng trọng trường và đàn hồi” dưới đây.
Thế năng là gì? Khái niệm thế năng
Trong chương trình giáo dục Vật lý, thế năng là một đại lượng thể hiện khả năng sinh công của vật. Tổng cộng sẽ có 3 loại thế năng đã được nghiên cứu bao gồm:
- Thế năng tĩnh điện.
- Thế năng đàn hồi.
- Thế năng trọng trường.
Thế nhưng theo chương trình học xuyên suốt từ Vật lý lớp 10 cho đến khi hết bậc phổ thông, các em học sinh sẽ không phải học đến thế năng tĩnh điện mà chỉ tập trung làm bài tập vận dụng xung quanh 2 thế năng là thế năng đàn hồi và thế năng trọng trường.
Thế năng đàn hồi là gì?
Khái niệm thế năng đàn hồi
Nếu như định nghĩa chung của thế năng là đại lượng thể hiện cho khả năng sinh công của vật. Vậy thì thế năng đàn hồi đó chính là đại lượng biểu hiện cho khả năng sinh lực đàn hồi của vật. Hãy ta vẫn có thể hiểu rằng đây là đại mang năng lượng của vật khi chịu tác động bởi lực đàn hồi.

Công thức tính thế năng đàn hồi
Công thức tính thế năng đàn hồi của một lò xo ở trạng thái có biến dạng Dℓ là:
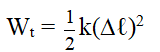
Trong đó:
- Wt là thế năng đàn hồi, đơn vị đo là J (Jun)
- k là độ cứng của lò xo, đơn vị đo là N.m
- ∆l là độ biến dạng của lò xo, đơn vị đo là m
Ví dụ thế năng đàn hồi
Thực tế, thế năng đàn hồi hiện diện hằng ngày trong cuộc sống của chúng ta. Miễn là hiện tượng đảm báo đáp ứng được sự xuất hiện của lực đàn hồi và độ biến dạng của vật là nơi đó có thế năng đàn hồi. Một số ví dụ quen thuộc mà ta có thể nhắc đến như:
- Dây cung được kéo căng.
- Quả bóng được bóp chặt.
- Lò xo bị đè nén.

Thế năng trọng trường là gì?
Khái niệm thế năng trọng trường
Bên cạnh thế năng đàn hồi thì thế năng trọng trường là đại lượng mà chúng ta gặp vô cùng thường xuyên trong cuộc sống. Từ 2 khái niệm được đề cập phía trên, các bạn học sinh chắc cũng đã mường tượng được khái niệm của thế năng trọng trường rồi nhỉ? Nếu như thế năng đàn hồi gắn liền với lực đàn hồi của lò xo thì thế năng trọng trường sẽ gắn liền với lực hút của Trái đất (trọng trường).

Công thức tính thế năng trọng trường
Vậy thì làm sao để có thể tính được thế năng trọng trường? Bạn chỉ cần sử dụng 2 công thức đơn giản và dễ nhớ cho 2 trường hợp sau đây:
Thế năng trọng trường của một vật thể bất kỳ có khối lượng m đặt ở vị trí cách mốc thế năng một khoảng z trong môi trường trọng trường, được tính theo công thức sau:
Wt =m.g.z
Trong đó
- Wt là thế năng trọng trường của thể vật tại vị trí đang xét, đơn vị đo là J (Jun)
- m là khối lượng của vật thể, đơn vị đo là kg
- z là khoảng cách từ vật đến mốc thế năng, đơn vị đo là m
- g là độ lớn gia tốc rơi tự do của vật thể, đơn vị đo là m/s2
Mốc thế năng là vị trí ban đầu của vật trong trọng trường trước khi sinh công. Ví dụ như khi vật được ném lên không trung. Lúc này, vị trí được ném lên cao nhất chính là mốc thế năng.
Các trường hợp có thể xảy ra là:
- Wt > 0
- Wt = 0
- Wt < 0
- z > 0 khi vật ở trên mốc thế năng.
- z <0 khi vật ở dưới mốc thế năng.
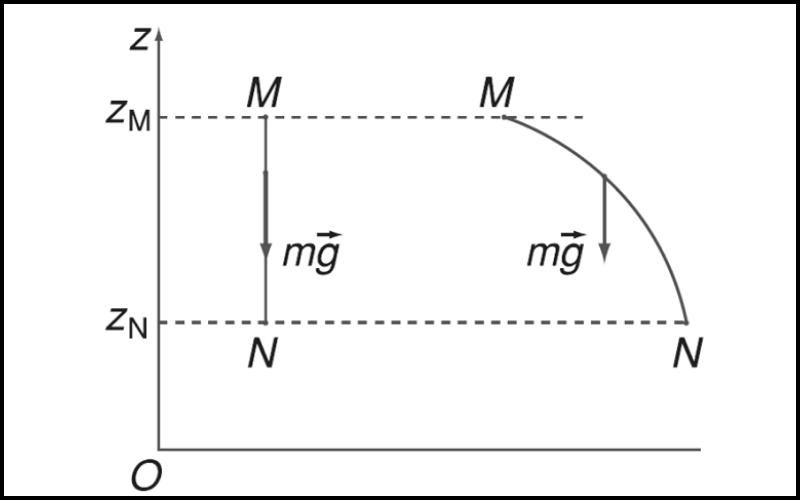
Sự biến thiên hay sự thay đổi của thế năng và công của trọng lực phụ thuộc vào vị trí của vật ở các thời điểm khác nhau. Khi vật thể di chuyển từ vị trí M đến vị trí N trong trọng trường (tăng độ cao hoặc giảm độ cao), công của trọng lực sẽ bằng với hiệu thế năng giữa 2 vị trí và được tính theo công thức
AMN = Wt(M) – Wt(N).
Ví dụ thế năng trọng trường
Bạn có thể bắt gặp thế năng trọng trường ngay xung quanh cuộc sống thường nhật như:
- Quả táo theo trọng lực bị rơi từ trên cây xuống dưới đất.
- Làm rơi quả bóng từ trên cao xuống.
- Quả bóng đứng im trên mặt bàn.
Bài tập về thế năng có đáp án
Bài tập 1. Một vật có khối lượng 1 kg đang ở cách mặt đất một khoảng H=20 m. Ở chân đường thẳng đứng đi qua vật có một cái hố sâu h=5 m. Cho g=10 m/s2.
a) Tính thế năng của vật khi chọn gốc thế năng là đáy hố.
b) Cho vật rơi không vận tốc ban đầu, tìm vận tốc của vật khi chạm đáy hố. Bỏ qua sức cản của không khí.
c) Với gốc thế năng là mặt đất thì thế năng của vật khi nằm ở đáy hố bằng bao nhiêu?
Lời giải bài tập 1
a) Với gốc thế năng là đáy hố:
z=H + h=25 m; W
=mgz=1*25*10=250 J.
b) Theo định luật bảo toàn cơ năng:
mgz1 + 0,5mv12=mgz2 + 0,5mv22
vì v1=0 ; z1=z ; z2=0
nên: mgz – 0,5mv22
<=> v2=
=22,4 m/s.
c) Với gốc thế năng ở mặt đất: z=- h=- 5 m; W
=mgz=- 50 J.
Bài tập 2. Từ độ cao 180 m, người ta thả rơi một vật nặng không vận tốc ban đầu. Bỏ qua sức cản không khí. Lấy g=10 m/s2. Xác định:
a) Độ cao mà ở đó thế năng bằng động năng và tính vận tốc của vật ở độ cao đó.
b) Vận tốc của vật lúc chạm đất.
Lời giải bài tập 2
Chọn gốc thế năng ở mặt đất.
a) Vị trí mà thế năng bằng động năng:
mgz1=mgz2 + 0,5mv22=2mgz2
<=> z2=z1/2=90 m;
mgz2=0,5mv22
<=> v2 = 42,4 m/s.
b) Vận tốc của vật lúc chạm đất:
mgz1=0,5mv32
<=> v3=60 m/s.
Bài tập 3: Chọn gốc thế năng ở mặt đất.
a) Vị trí mà thế năng bằng động năng:
mgz1=mgz2 + 0,5mv22=2mgz2
<=> z2=z1/2=90 m;
mgz2=0,5mv22
<=> v2 = 42,4 m/s.
b) Vận tốc của vật lúc chạm đất:
mgz1=0,5mv32
<=>v3=60 m/s.
Lời giải bài tập 3:
Chọn gốc thế năng ở mặt đất.
a) Vị trí mà thế năng bằng động năng:
mgz1=mgz2 + 0,5mv22=2mgz2
<=> z2=z1/2=90 m;
mgz2=0,5mv22
<=> v2 = 42,4 m/s.
b) Vận tốc của vật lúc chạm đất:
mgz1=0,5mv32
<=> v3=60 m/s.
Bài tập 4: Chọn gốc thế năng ở mặt đất.
a) Vị trí mà thế năng bằng động năng:
mgz1=mgz2 + 0,5mv22=2mgz2
<=> z2=z1/2=90 m;
mgz2=0,5mv22
<=> v2 = 42,4 m/s.
b) Vận tốc của vật lúc chạm đất:
mgz1=0,5mv32
<=> v3=60 m/s.
Lời giải bài tập 4
Chọn gốc thế năng ở mặt đất.
a) Vị trí mà thế năng bằng động năng:
mgz1=mgz2 + 0,5mv22=2mgz2
<=> z2=z1/2=90 m;
mgz2=0,5mv22
<=> v2 = 42,4 m/s.
b) Vận tốc của vật lúc chạm đất:
mgz1=0,5mv32
<=> v3=60 m/s.
Bài tập 5:
Một khẩu súng đồ chơi có một lò xo dài 10 cm, lúc bị nén chỉ còn dài 4 cm thì có thể bắn thẳng đứng một viên đạn có khối lượng 30 g lên cao 6 m. Tìm độ cứng của lò xo.
Lời giải bài tập 5
Theo định luật bảo toàn cơ năng:
0,5kΔl2=mgz
<=> k=
= 1000 N/m.[/i]
Bài tập 6: Từ độ cao 25 m người ta ném thẳng đứng một vật nặng lên cao với vận tốc ban đầu bằng 20 m/s. Bỏ qua sức cản không khí. Lấy g=10 m/s2. Tính:
a) Độ cao cực đại mà vật đạt được.
b) Độ cao mà ở đó thế năng bằng nữa động năng và vận tốc của vật ở độ cao đó.
Lời giải bài tập 6:
Chọn gốc thế năng ở mặt đất.
a) Ở độ cao cực đại (v=0): mgz
=mgz1 + 0,5mv12
<=> z
=45 m.
b) Ở độ cao thế năng bằng nữa động năng (mgz2=0,5.0,5mv22):
mgz
=mgz2 + 0,5mv22=3mgz
z2=15 m;
mgz2 =0,5. 0,5mv22
<=> v2=24,5 m/s.
Bài tập 8:Một vật có khối lượng m=3 kg được đặt ở một vị trí trong trọng trường và thế năng tại vị trí đó bằng wt1t1=600 J. Thả tự do cho vật rơi tới mặt đất, tại đó thế năng của vật bằng wt2t2=- 900 J.
a) Hỏi vật đã rơi từ độ cao nào so với mặt đất?
b) Xác định vị trí ứng với mức 0 của thế năng đã chọn và tìm vận tốc của vật khi đi qua vị trí này.
Lời giải bài tập 8
a) Độ cao so với vị trí chọn mốc thế năng:
z1=
=20 m.
Vị trí của mặt đất so với vị trí chọn mốc thế năng:
z2=
=- 30 m.
Độ cao từ đó vật đã rơi so với mặt đất: z=z1 + |z2|=50 m.
b) Vị trí ứng với mức không của thế năng được chọn cách vị trí thả vật (ở phía dưới vị trí thả vật) 20 m và cách mặt đất (ở phía trên mặt đất) 30 m.
Vận tốc của vật khi đi qua vị trí được chọn làm gốc thế năng:
mgz1=mv=> v
= 20 m/s.
Xem thêm:
- Sơ đồ nguyên lý là gì? Sơ đồ lắp đặt là gì? Cách vẽ và ví dụ minh họa
- Bộ đề cương ôn tập vật lý 7 học kỳ 2
- Tổng hợp bộ đề thi giữa kì 1 toán 6 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
Bài viết trên là tổng hợp toàn bộ thông tin về khái niệm thế năng, công thức tính thế năng trọng trường và đàn hồi cùng các bài tập bổ trợ. Mong là những kiến thức trên sẽ giúp các em học sinh có bước đi vững chắc và dễ dàng tiếp thu kiến thức Vật Lý 10 này nhé! Và đừng quên hãy thường xuyên ghé thăm Bamboo School để cập nhật thêm thật nhiều kiến thức các bộ môn cùng bài tập đầy đủ cho 12 khối lớp từ cơ bản đến nâng cao.
Tổng hợp đề thi ngữ văn lớp 6 giữa kì 1 chương trình mới có đáp án
Sắp đến kì thi giữa kì 1, chắc hẳn các bạn học sinh đang rất bận rộn để ôn luyện các dạng đề môn ngữ văn lớp 6. Để các bạn có thể làm bài thi giữa kì tốt nhất thì dưới đây là 3 bộ đề thi ngữ văn lớp 6 giữa học kì 1 theo chương trình mới Trung học Cơ sở có kèm theo đáp án mà Bamboo School đã tổng hợp từ ba bộ sách khác nhau như sách Cánh diều, Chân trời sáng tạo và Kết nối tri thức. Hy vọng với 3 bộ đề thi này sẽ giúp các bạn học sinh ôn tập hiệu quả, nắm được cách ra đề thi và các dạng bài cần lưu ý để đạt kết quả cao trong các bài thi sắp tới.
Đề kiểm tra giữa kì 1 văn 6 Cánh diều
I. ĐỌC HIỂU (6.0 điểm)
Đọc văn bản sau và trả lời các câu hỏi:
SỰ TÍCH HOA CÚC TRẮNG
Ngày xưa, có một gia đình nghèo gồm hai mẹ con sống nương tựa vào nhau, cuộc sống của họ bình yên trong một ngôi nhà nhỏ. Người mẹ hàng ngày tần tảo làm lụng nuôi con. Người con thì cũng hiếu thảo, biết vâng lời mẹ và chăm chỉ học hành. Một ngày kia, người mẹ bỗng lâm bệnh nặng, mặc dù người con rất thương mẹ, chạy chữa biết bao thầy lang giỏi trong vùng cũng không chữa khỏi cho mẹ. Em buồn lắm, ngày ngày đều cầu phúc cho mẹ. Thương mẹ, người con quyết tâm đi tìm thầy nơi khác về chữa bệnh. Người con đi mãi, qua bao nhiêu làng mạc, núi sông, ăn đói mặc rách vẫn không nản lòng.
Đến một hôm, khi đi ngang qua một ngôi chùa, em xin nhà sư trụ trì được vào thắp hương cầu phúc cho mẹ. Lời cầu xin của em khiến trời nghe cũng phải nhỏ lệ, đất nghe cũng cúi mình. Lời cầu xin đó đến tai Đức Phật từ bi, Người cảm thương tấm lòng hiếu thảo đó của em nên đã tự mình hóa thân thành một nhà sư. Nhà sư đi ngang qua chùa và tặng em một bông hoa trắng rồi nói:
– Bông hoa này là biểu tượng của sự sống, là bông hoa chứa đựng niềm hi vọng, là ước mơ của loài người, là thần dược để chữa bệnh cho mẹ con, con hãy mang nó về chăm sóc. Nhưng phải nhớ rằng, cứ mỗi năm sẽ có một cánh hoa rụng đi và bông hoa có bao nhiêu cánh thì mẹ con chỉ sống được bấy nhiêu năm. Nói rồi nhà sư biến mất.
Em nhận bông hoa, cảm tạ Đức Phật, lòng em rất đỗi vui mừng. Nhưng khi đếm những cánh hoa, lòng em bỗng buồn trở lại khi biết rằng bông hoa chỉ có năm cánh, nghĩa là mẹ em chỉ sống được thêm với em có năm năm nữa. Thương mẹ quá, em nghĩ ra một cách, em liền liều xé nhỏ những cánh hoa ra thành nhiều cánh nhỏ, nhiều đến khi không còn đếm được bông hoa có bao nhiêu cánh nữa. Nhờ đó mà mẹ em đã khỏi bệnh và sống rất lâu bên người con hiếu thảo của mình. Bông hoa trắng với vô số cánh nhỏ đó đã trở thành biểu tượng của sự sống, là ước mơ trường tồn, là sự hiếu thảo của người con đối với mẹ, là khát vọng chữa lành mọi bệnh tật cho mẹ của người con. Ngày nay, bông hoa đó được người đời gọi là hoa cúc trắng.
(Phỏng theo Truyện cổ tích Nhật Bản – Sách Ngựa Gióng)
Lựa chọn đáp án đúng nhất:
Câu 1. Truyện Sự tích hoa cúc trắng thuộc thể loại nào?
A. Truyện cổ tích
B. Truyện đồng thoại
C. Truyền thuyết
D. Thần thoại
Câu 2. Câu chuyện trên được kể theo ngôi thứ mấy?
A.Ngôi thứ nhất
B. Ngôi thứ ba
C. Ngôi thứ hai
D. Cả ngôi thứ nhất và ngôi thứ ba
Câu 3. Trong câu chuyện, em bé cứu sống được mẹ là nhờ tìm được thầy lang giỏi, theo em đúng hay sai?
A. Đúng
B. Sai
Câu 4. Theo nhà sư, bông hoa cúc trắng biểu tượng cho điều gì?
A. Biểu tượng cho sự sống và lòng hiếu thảo
B. Biểu tượng cho sự sống và lòng kiên trì
C. Biểu tượng cho sự sống và tình yêu thương
D. Biểu tượng cho sự sống và ước mơ cao đẹp
Câu 5. Vì sao em bé lại xé nhỏ các cánh hoa?
A. Vì em vốn là đứa trẻ hiếu động
B. Vì em nghĩ bông hoa nhiều cánh sẽ đẹp hơn
C. Vì em bé muốn mẹ sống lâu bên mình
D. Vì em thích bông hoa nhiều cánh
Câu 6. Trong câu văn“Người mẹ hàng ngày tần tảo làm lụng nuôi con”, từ láy tần tảo có ý nghĩa là:
A. Làm lụng chăm chỉ công việc nhà trong hoàn cảnh khó khăn
B. Làm lụng chăm chỉ công việc đồng áng trong hoàn cảnh khó khăn
C. Làm lụng chăm chỉ việc nhà và đồng áng trong hoàn cảnh khó khăn
D. Làm lụng vất vả, lo toan việc nhà trong hoàn cảnh khó khăn
Câu 7. “Ngày xưa, có một gia đình nghèo gồm hai mẹ con sống nương tựa vào nhau, cuộc sống của họ bình yên trong một ngôi nhà nhỏ”. Từ in đậm trong câu văn thuộc loại trạng ngữ nào?
A. Trạng ngữ chỉ mục đích
B. Trạng ngữ chỉ nơi chốn
C. Trạng ngữ chỉ nguyên nhân
D. Trạng ngữ chỉ thời gian
Câu 8. Chủ đề nào sau đây đúng với truyện Sự tích hoa cúc trắng?
A. Ca ngợi ý nghĩa các loài hoa
B. Ca ngợi tình mẫu tử
C. Ca ngợi tình cảm gia đình
D. Ca ngợi tình cha con
Thực hiện yêu cầu:
Câu 9. Hãy rút ra bài học mà em tâm đắc nhất sau khi đọc câu chuyện trên.
Câu 10. Qua câu chuyện, em thấy mình cần phải có trách nhiệm gì với cha mẹ?
II. VIẾT (4.0 điểm)
Hãy kể lại một truyện truyền thuyết bằng lời văn của em.
Đáp án đề kiểm tra giữa kì 1 văn 6 Cánh diều
I. ĐỌC HIỂU (6.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Đáp án | A | B | B | A | C | D | D | B |
| Điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm |
Câu 9. (1 điểm)
Bài học tâm đắc nhất sau khi em đọc câu chuyện trên là: Hãy luôn nỗ lực, hướng đến tương lai, tin tưởng vào sự sống và hiểu thảo với cha mẹ thì những điều tốt đẹp sẽ đến với bạn bằng nhiều cách khác nhau. Và đừng bao giờ từ bỏ hy vọng mà hãy luôn tìm kiếm, nỗ lực để đạt được điều bản thân mong muốn.
Câu 10. (1 điểm)
Qua câu truyện trên, em thấy mình cần phải có trách nhiệm chăm sóc cha mẹ khi đau ốm, hiểu thảo cha mẹ và không làm cha mẹ buồn phiền hay vất vả.
II. VIẾT (4.0 điểm)
a. Đảm bảo cấu trúc bài văn tự sự (0,25 điểm)
b. Xác định đúng yêu cầu của đề là “Kể lại một truyện truyền thuyết bằng lời văn của em” (0,25 điểm)
c. Kể lại một truyện truyền thuyết bằng lời văn của em. (2,5 điểm)
Có thể triển khai cốt truyện theo nhiều cách, nhưng cần đảm bảo các yêu cầu sau:
- Sử dụng ngôi kể phù hợp.
- Giới thiệu được câu chuyện truyền thuyết định kể.
- Giới thiệu được nhân vật chính, các sự kiện chính trong truyền thuyết: bắt đầu – diễn biến – kết thúc.
- Ý nghĩa của truyện truyền thuyết.
d. Đảm bảo chuẩn chính tả, ngữ pháp Tiếng Việt. (0,5 điểm)
e. Sáng tạo: Bố cục mạch lạc, lời kể sinh động, sáng tạo. (0,5 điểm)
Bài văn mẫu “Kể lại truyền thuyết Thánh Gióng” mà học sinh có thể tham khảo:
Ngày xửa ngày xưa, vào thời vua Hùng Vương thứ mười sáu, có một đôi vợ chồng tuy đã già nhưng vẫn chẳng có lấy một mụn con. Hai ông bà lão nổi tiếng là người hiền lành, đôn hậu ở làng Gióng nhưng không hiểu sao lại chịu sự không may mắn như vậy. Cho đến một ngày, khi bà lão đi ra đồng thì chợt thấy một dấu chân to khổng lồ. Lấy làm ngạc nhiên, bà lão đưa chân mình vào ướm thử để đo xem dấu vết chân đó to đến cỡ nào. Thời gian thấm thoát trôi đi, bà lão chẳng còn nhớ đến vết chân ngày xưa nữa thì bỗng một ngày bà có thai. Hai vợ chồng bà lão mừng lắm, bà sinh ra một cậu bé khôi ngô, tuấn tú. Ấy thế mà đứa trẻ đó từ khi sinh ra lại chẳng biết nói, cũng không biết cười, không biết đi, chỉ đặt đâu thì nó nằm đấy. Hai ông bà từ mừng rỡ khi sinh được con đến lo lắng, buồn bã không hiểu sao lại như vậy.
Lúc bấy giờ, giặc Ân tràn sang xâm lược nước ta. Chúng khiến cho đời sống nhân dân vô cùng khổ cực, tình cảnh đất nước lúc này đang ở thế “nghìn cân treo sợi tóc”. Nhà vua sai sứ giả đi rao tin khắp nơi, nhằm tìm người tài đứng lên cứu giúp đất nước. Sứ giả đi rao tin cuối cùng cũng đến làng Gióng. Nghe tiếng sứ giả, cậu bé bỗng nhiên cất tiếng gọi mẹ: “Mẹ ơi, mẹ hãy mời sứ giả vào đây cho con”. Thấy đứa con mình suốt bao nhiêu ngày tháng không nói, không cười bỗng dưng hôm nay lại cất tiếng gọi mẹ, hai ông bà lão mừng lắm, liền mời sứ giả vào ngay.
Khi sứ giả vào nhà, cậu bé đã ngay lập tức yêu cầu sứ giả hãy về chuẩn bị đủ những vũ khí để đi đánh giặc: Ngựa sắt, áo sắt và tấm giáp sắt để phá tan lũ giặc xâm lược. Sứ giả mừng rỡ vội về tâu lên cho nhà vua chuẩn bị. Nhà vua cũng đồng ý theo lời của cậu bé.Càng lạ lùng thay, Thánh Gióng từ khi gặp được sứ giả của nhà vua thì lớn nhanh như thổi, cơm cha mẹ thổi bao nhiêu cậu ăn cũng không đủ no, quần áo chẳng mấy chốc đều chật hết cả. Cậu bé chẳng mấy chốc hóa thành một chàng trai cao lớn, khỏe mạnh, khí thế ngút trời.
Chẳng bao lâu, nhà mua sai người đem đến đủ cả những thứ mà Gióng yêu cầu. Thánh Gióng lên đường đánh giặc ngay. Cậu đi đến đâu đánh bại quân giặc đến đấy. Khi kiếm gãy, Gióng liền nhổ một bụi cỏ bên đường, quật ngã bọn giặc ngoại xâm. Một hồi, ngựa của Thánh Gióng đã đến chân núi Sóc Sơn, Thánh Gióng liền cởi bộ giáp sắt đang mặc trên người ra mà bay thẳng lên trời.
Để nhớ đến công lao của Thánh Gióng, nhà vua đã cho người lập đền thờ của vị tướng này tại quê nhà của ông là làng Gióng. Cho đến nay, vẫn còn rất nhiều dấu tích năm xưa còn lưu lại và cứ tháng 4 hằng năm, người ta vẫn thường đến đền thờ Phù Đổng Thiên Vương để tưởng nhớ ông.
Đề thi Ngữ văn lớp 6 giữa học kì 1 Chân trời sáng tạo
I. ĐỌC HIỂU (6.0 điểm)
Đọc văn bản sau:
SỰ TÍCH CÂY NGÔ
Năm ấy, trời hạn hán. Cây cối chết khô vì thiếu nước, bản làng xơ xác vì đói khát. Nhiều người phải bỏ bản ra đi tìm nơi ở mới. Ở nhà nọ chỉ có hai mẹ con. Người mẹ ốm đau liên miên và cậu con trai lên 7 tuổi. Cậu bé tên là Aưm, có nước da đen nhẫy và mái tóc vàng hoe. Tuy còn nhỏ nhưng Aưm đã trở thành chỗ dựa của mẹ. Hằng ngày, cậu dậy sớm vào rừng kiếm măng, hái nấm, hái quả mang về cho mẹ. Nhưng trời ngày càng hạn hán hơn. Có những lần cậu đi cả ngày mà vẫn không tìm được thứ gì để ăn. Một hôm, vừa đói vừa mệt cậu thiếp đi bên bờ suối. Trong mơ, cậu nhìn thấy một con chim cắp quả gì to bằng bắp tay, phía trên có chùm râu vàng như mái tóc của cậu. Con chim đặt quả lạ vào tay Aưm rồi vỗ cánh bay đi. Tỉnh dậy Aưm thấy quả lạ vẫn ở trên tay. Ngạc nhiên, Aưm lần bóc các lớp vỏ thì thấy phía trong hiện ra những hạt màu vàng nhạt, xếp thành hàng đều tăm tắp. Aưm tỉa một hạt bỏ vào miệng nhai thử thì thấy có vị ngọt, bùi. Mừng quá, Aưm cầm quả lạ chạy một mạch về nhà.
Mẹ của cậu vẫn nằm thiêm thiếp trên giường. Thương mẹ mấy ngày nay đã đói lả, Aưm vội tỉa những hạt lạ đó mang giã và nấu lên mời mẹ ăn. Người mẹ dần dần tỉnh lại, âu yếm nhìn đứa con hiếu thảo. Còn lại ít hạt, Aưm đem gieo vào mảnh đất trước sân nhà. Hằng ngày, cậu ra sức chăm bón cho cây lạ. Nhiều hôm phải đi cả ngày mới tìm được nước uống nhưng Aưm vẫn dành một gáo nước để tưới cho cây. Được chăm sóc tốt nên cây lớn rất nhanh, vươn những lá dài xanh mướt. Chẳng bao lâu, cây đã trổ hoa, kết quả.
Mùa hạn qua đi, bà con lũ lượt tìm về bản cũ. Aưm hái những quả lạ có râu vàng hoe như mái tóc của cậu biếu bà con để làm hạt giống. Quý tấm lòng thơm thảo của Aưm, dân bản lấy tên câu bé đặt tên cho cây có quả lạ đó là cây Aưm, hay còn gọi là cây ngô. Nhờ có cây ngô mà từ đó, những người dân Pako không còn lo thiếu đói nữa.
(Truyện cổ tích Việt Nam – Nguồn truyencotich.vn)
Lựa chọn đáp án đúng nhất:
Câu 1. Truyện Sự tích cây ngô thuộc thể loại nào?
A. Truyện cổ tích
B. Truyện đồng thoại
C. Truyền thuyết
D. Thần thoại
Câu 2. Câu chuyện trên được kể theo ngôi thứ mấy?
A. Ngôi thứ nhất
B. Ngôi thứ ba
C. Ngôi thứ hai
D. Cả ngôi thứ nhất và ngôi thứ ba
Câu 3. Trong câu chuyện, em bé cứu sống được mẹ là nhờ tìm được thầy lang giỏi, theo em đúng hay sai?
A. Đúng
B. Sai
Câu 4. Theo em, cây ngô biểu tượng cho điều gì của dân làng Pako?
A. Biểu tượng cho sự sống và lòng hiếu thảo
B. Biểu tượng cho sự sống và tình yêu thương
C. Biểu tượng cho sự sống ấm no của dân làng
D. Biểu tượng cho sự sống và ước mơ cao đẹp
Câu 5. Vì sao em bé lại đem giống ngô cho mọi người?
A. Vì em nghĩ mọi người đều thương yêu em
B. Vì em bé muốn mẹ được khỏe mạnh
C. Vì em thích loại giống lạ mới thấy lần đầu
D. Vì em có lòng tốt muốn chia sẻ cho dân làng
Câu 6. Chủ đề nào sau đây đúng với truyện Sự tích cây ngô?
A. Ca ngợi ý nghĩa của loài cây
B. Ca ngợi lòng hiếu thảo
C. Ca ngợi tình cảm gia đình
D. Ca ngợi tình mẫu tử
Câu 7. Trong câu văn “Mùa hạn qua đi, bà con lũ lượt tìm về bản cũ”, từ lũ lượt là từ gì?
A. Từ láy
B. Từ nhiều nghĩa
C. Từ ghép
D. Từ đồng âm
Câu 8. “Hằng ngày, cậu dậy sớm vào rừng kiếm măng, hái nấm, hái quả mang về cho mẹ.” Từ in đậm trong câu văn thuộc loại trạng ngữ nào?
A. Trạng ngữ chỉ thời gian
B. Trạng ngữ chỉ mục đích
C. Trạng ngữ chỉ nơi chốn
D. Trạng ngữ chỉ nguyên nhân
Thực hiện yêu cầu:
Câu 9. Hãy rút ra bài học mà em tâm đắc nhất sau khi đọc câu chuyện trên.
Câu 10. Qua câu chuyện, em thấy mình cần phải có trách nhiệm gì với cha mẹ và cộng đồng?
II. VIẾT (4.0 điểm)
Hãy kể lại một truyện truyền thuyết bằng lời văn của em.
Đáp án đề thi Ngữ văn lớp 6 giữa học kì 1 Chân trời sáng tạo
I. ĐỌC HIỂU (6.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Đáp án | A | B | B | C | D | B | C | A |
| Điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm |
Câu 9. (1 điểm)
Bài học mà em tâm đắc nhất sau khi đọc câu chuyện trên là: Hãy biết hiếu thảo, chăm sóc cha mẹ khi đau ốm và biết chia sẻ với mọi người những thứ mà ta nhận được từ sự giúp đỡ của người khác.
Câu 10. (1 điểm)
Qua câu chuyện trên, em thấy bản thân cần có trách nhiệm hiếu thảo, chăm lo cho cha mẹ khi đau ốm hay già yếu và biết chia sẻ, giúp đỡ mọi người để cùng nhau vượt qua khó khăn, cùng nhau phát triển.
II. VIẾT (4.0 điểm)
a. Đảm bảo cấu trúc bài văn tự sự (0,25 điểm)
b. Xác định đúng yêu cầu của đề là “Kể lại một truyện truyền thuyết bằng lời văn của em” (0,25 điểm)
c. Kể lại một truyện truyền thuyết bằng lời văn của em. (2,5 điểm)
Có thể triển khai cốt truyện theo nhiều cách, nhưng cần đảm bảo các yêu cầu sau:
- Sử dụng ngôi kể phù hợp.
- Giới thiệu được câu chuyện truyền thuyết định kể.
- Giới thiệu được nhân vật chính, các sự kiện chính trong truyền thuyết: bắt đầu – diễn biến – kết thúc.
- Ý nghĩa của truyện truyền thuyết.
d. Đảm bảo chuẩn chính tả, ngữ pháp Tiếng Việt. (0,5 điểm)
e. Sáng tạo: Bố cục mạch lạc, lời kể sinh động, sáng tạo. (0,5 điểm)
Bài văn mẫu “Kể lại truyền thuyết Sự tích Hồ Gươm” mà học sinh có thể tham khảo:
Thời giặc Minh đặt ách đô hộ ở nước Nam, chúng coi dân như cỏ rác, tác oai tác quái làm nhiều điều trái với đạo lý. Nghĩa quân Lam Sơn nhiều lần đứng lên chống giặc nhưng đều bị thất bại.
Thấy vậy Đức Long Quân quyết định cho nghĩa quân mượn Gươm thần để đánh giặc. Thời ấy ở Thanh Hoá có chàng trai tên là Lê Thận làm nghề đánh cá. Một đêm, Thận thả lưới trên bến vắng, ba lần kéo lưới lên đều thấy một thanh sắt, chàng trai nhận ra đó là lưỡi gươm liền đem về cất ở xó nhà. Sau đó Lê Thận hăng hái gia nhập nghĩa quân Lam Sơn. Một hôm, chủ tướng Lê Lợi cùng tuỳ tùng đến nhà Thận, thấy thanh gươm tự nhiên sáng rực lên, Lê Lợi bèn cầm lên xem thây có hai chữ “Thuận Thiên”.
Một lần khi bị thua phải tháo chạy Lê Lợi đi qua khu rừng, thấy chuôi gươm nạm ngọc trên ngọn cây đa tỏa ánh sáng, nhớ tới lưỡi gươm ở nhà Thận Lê Lợi giắt vào lưng đem về. Ba ngày sau, Lê Lợi gặp lại mọi người đã kể lại chuyện bắt được chuôi gươm. Lê Thận đem gươm ra tra vào chuôi thì vừa khớp với nhau. Lê Thận nâng gươm trao cho Lê Lợi và nói rằng đây là Trời có ý phó thác cho minh công làm việc lớn. Lê Lợi với thanh gươm báu cùng nhuệ khí nghĩa quân ngày một lớn mạnh. Trên các trận đánh làm quân Minh kinh hồn bạt vía.
Uy danh của nghĩa quân vang dội khắp nơi. Chiến lợi phẩm thu về ngày càng nhiều. Thế chủ động tấn công ngày một cao, chẳng mấy chốc đã đuổi được sạch bóng giặc Minh khỏi bờ cõi. Một năm sau khi đuổi giặc Minh, vua Lê Lợi cưỡi thuyền rồng dạo quanh hồ Tả Vọng. Nhân đó Long Quân sai Rùa vàng lên đòi lại thanh gươm thần. Thuyền rồng ra giữa hồ, thấy có Rùa lớn xuất hiện, vua truyền lệnh cho thuyền chậm lại. Rùa vàng tiến về phía vua và nói: “Xin bệ hạ hoàn gươm lại cho Long Quân”. Nghe Rùa vàng nói vua hiểu ý, rút gươm trả cho Rùa vàng. Rùa vàng lập tức há miệng đỡ lấy thanh gươm và từ từ chìm xuống nước.
Gươm và Rùa đã chìm xuống nước nhưng người ta thấy có ánh sáng loang loáng dưới mặt hồ xanh. Từ đó hồ Tả Vọng mang tên là hồ Gươm hay là hồ Hoàn Kiếm.
Đề thi Ngữ văn lớp 6 giữa học kì 1 Kết nối tri thức
Phần I. Đọc – hiểu (6.0 điểm)
Đọc kĩ đoạn trích sau và trả lời các câu hỏi bên dưới:
“Gió bắc thổi ào ào qua khu rừng vắng. Những cành cây khẳng khiu chốc chốc run lên bần bật. Mưa phùn lất phất… Bên gốc đa, một chú Thỏ bước ra, tay cầm một tấm vải dệt bằng rong. Thỏ tìm cách quấn tấm vải lên người cho đỡ rét, nhưng tấm vải bị gió lật tung, bay đi vun vút. Thỏ đuổi theo. Tấm vải rơi tròng trành trên ao nước. Thỏ vừa đặt chân xuống nước đã vội co lên. Thỏ cố khều nhưng đưa chân không tới. Một chú Nhím vừa đi đến. Thỏ thấy Nhím liền nói:
– Tôi đánh rơi tấm vải khoác!
– Thế thì gay go đấy! Trời rét, không có áo khoác thì chịu sao được.
Nhím nhặt chiếc que khều… Tấm vải dạt vào bờ, Nhím nhặt lên, giũ nước, quấn lên người Thỏ:
– Phải may thành một chiếc áo, có thế mới kín được.
– Tôi đã hỏi rồi. Ở đây chẳng có ai may vá gì được.
Nhím ra dáng nghĩ:
– Ừ! Muốn may áo phải có kim. Tôi thiếu gì kim.
Nói xong, Nhím xù lông. Quả nhiên vô số những chiếc kim trên mình Nhím dựng lên nhọn hoắt. Nhím rút một chiếc lông nhọn, cởi tấm vải trên mình Thỏ để may.
(Trích “Những chiếc áo ấm”, Võ Quảng)
Hãy chọn đáp án đúng nhất để trả lời câu hỏi: (Mỗi câu đúng được 0.5 điểm)
Câu 1: Thể loại của đoạn trích trên là:
A. Truyện cổ tích
B. Truyện đồng thoại
C. Truyện truyền thuyết
D. Truyện ngắn
Câu 2: Đoạn trích trên được kể bằng lời của ai?
A. Lời của người kể chuyện
B. Lời của nhân vật Nhím
C. Lời của nhân vật Thỏ
D. Lời của Nhím và Thỏ
Câu 3: Nhận xét nào nêu lên đặc điểm của nhân vật trong văn bản trên?
A. Nhân vật là loài vật, sự vật được nhân cách hóa như con người.
B. Nhân vật là loài vật, sự vật có liên quan đến lịch sử.
C. Nhân vật là loài vật, sự vật có những đặc điểm kì lạ.
D. Nhân vật là loài vật, sự vật gắn bó thân thiết với con người như bạn.
Câu 4: Em hiểu nghĩa của từ “tròng trành” trong câu “Tấm vải rơi tròng trành trên ao nước.” là gì?
A. Quay tròn, không giữ được thăng bằng.
B. Ở trạng thái nghiêng qua nghiêng lại.
C. Ở trạng thái nghiêng qua nghiêng lại, không giữ được thăng bằng.
D. Ở trạng thái quay tròn, nghiêng qua nghiêng lại.
Câu 5: Thỏ đã gặp sự cố gì trong đoạn trích trên?
A. Bị ngã khi cố với một chiếc khăn.
B. Tấm vải của Thỏ bị gió cuốn đi, rơi trên ao nước.
C. Bị thương khi cố khều tấm vải mắc trên cây.
D. Đi lạc vào một nơi đáng sợ.
Câu 6: Có bao nhiêu từ láy trong đoạn văn sau?
“Gió bấc thổi ào ào qua khu rừng vắng. Những cành cây khẳng khiu chốc chốc run lên bần bật. Mưa phùn lất phất… Bên gốc đa, một chú Thỏ bước ra, tay cầm một tấm vải dệt bằng rong. Thỏ tìm cách quấn tấm vải lên người cho đỡ rét, nhưng tấm vải bị gió lật tung, bay đi vun vút.”
A. Bốn từ
B. Năm từ
C. Sáu từ
D. Bảy từ
Câu 7: Từ ghép trong câu văn “Nhím rút một chiếc lông nhọn, cởi tấm vải trên mình Thỏ để may” là những từ nào?
A. Nhím rút, tấm vải
B. Một chiếc, để may
C. Chiếc lông, tấm vải
D. Lông nhọn, trên mình
Câu 8: Điền từ thích hợp vào chỗ trống trong lời nhận xét sau để thể hiện đúng nhất thái độ của Nhím đối với Thỏ qua câu nói “Thế thì gay go đấy! Trời rét, không có áo khoác thì chịu sao được?”
Nhím……………. cho Thỏ.
A. Lo sợ
B. Lo lắng
C. Lo âu
D. Lo ngại
Thực hiện yêu cầu:
Câu 9 (1.0 điểm): Hãy chỉ ra và nêu tác dụng của biện pháp tu từ nhân hóa được sử dụng trong câu văn sau “Những cành cây khẳng khiu chốc chốc run lên bần bật”.
Câu 10 (2.0 điểm): Từ hành động của các nhân vật trong đoạn trích, em rút ra được những bài học đáng quý nào?
Phần II. Làm văn (4.0 điểm)
Viết bài văn (khoảng 1,5 trang giấy) kể lại trải nghiệm một lần em giúp đỡ người khác hoặc nhận được sự giúp đỡ từ những người xung quanh.
Đáp án đề thi Ngữ văn lớp 6 giữa học kì 1 Kết nối tri thức
Phần I. Đọc – hiểu (6.0 điểm)
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Đáp án | B | A | A | C | B | C | C | D |
| Điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm |
Câu 9. (1 điểm)
– Biện pháp tu từ nhân hóa: run lên bần bật.
– Tác dụng:
- Biện pháp nhân hóa đã làm cho hình ảnh cây cối trở nên sinh động, giống như con người, cũng cảm nhận được cái rét của gió bắc.
- Gợi tả khung cảnh mùa đông giá rét.
Câu 10. (1 điểm)
Học sinh nêu được những bài học phù hợp như:
- Có lòng nhân ái, yêu thương mọi người.
- Cần biết cảm thông, thấu hiểu, giúp đỡ người khác khi họ khó khăn.
- Nhanh nhẹn, linh hoạt khi gặp khó khăn, trở ngại.
Phần II. Làm văn (4.0 điểm)
a. Đảm bảo cấu trúc bài văn tự sự (0,25 điểm)
Đủ 3 phần mở bài, thân bài, kết bài; các ý được sắp xếp theo một trình tự hợp lí.
b. Xác định đúng yêu cầu của đề: Kể về một lần em giúp đỡ người khác hoặc nhận được sự giúp đỡ từ những người xung quanh (0,25 điểm)
c. Kể về một lần em giúp đỡ người khác hoặc nhận được sự giúp đỡ từ những người xung quanh (2,5 điểm)
Học sinh có thể triển khai cốt truyện theo nhiều cách, nhưng cần đảm bảo các yêu cầu sau:
- Sử dụng ngôi kể thứ nhất.
- Giới thiệu được trải nghiệm.
- Các sự kiện chính trong trải nghiệm: bắt đầu – diễn biến – kết thúc.
- Những ý nghĩa của trải nghiệm với bản thân.
d. Đảm bảo chuẩn chính tả, ngữ pháp Tiếng Việt. (0,5 điểm)
e. Sáng tạo: Bố cục rõ ràng, lời văn giàu hình ảnh, cảm xúc (0,5 điểm)
Bài văn mẫu mà bạn có thể tham khảo:
Vì vội vã mà em không kịp ăn sáng, em cầm chiếc bánh mì mẹ vội đưa mà vừa chạy vừa ăn, trong lòng chỉ mong sao cho mình đến kịp giờ, đến muộn nếu làm ảnh hưởng đến thành tích thi đua của cả lớp thì em sẽ rất áy náy. Sau khi chạy hết sức mình thì cuối cùng hình ảnh của cánh cổng trường cũng hiện ra trước mắt em. Nhưng để vào trường thì em phải băng qua một tuyến đường, sáng sớm đúng giờ mọi người đi làm nên xe cộ khá đông đúc, mặt khác đoạn đường này chưa được lắp đặt hệ thống đèn đỏ nên gây khó khăn lớn cho việc sang đường.
Em định băng qua đường để vào trường nhưng em chợt nhìn sang bên cạnh có một bà cụ đang đi tới, có vẻ cụ cũng đang định sang đường, xe cộ đông như vậy nếu để cụ đi một mình thì sẽ rất nguy hiểm. Nghĩ vậy em liền bước tới gần cụ và nắm lấy cánh tay của cụ:
“Cụ để con dẫn cụ qua đường nhé, bây giờ xe đông cụ qua đường sẽ rất nguy hiểm”, nghe em nói, cụ hướng đôi mắt về phía em, ánh mắt cụ đục đục vì tuổi già nhưng lại ánh lên vẻ hiền từ, nhân hậu. Nhìn cụ em lại nhớ về bà của mình, cụ ôn tồn nói với em:
“Cảm ơn cháu nhé, cháu thật tốt bụng”, nghe cụ nói em có chút ngượng ngùng, em cho rằng hành động này là tất nhiên, ai nhìn thấy cũng sẽ hành động như em thôi, chứ lời khen tốt bụng của bà cụ thì em chưa xứng đáng để nhận.
“Dạ không có gì đâu cụ ạ, để con dẫn cụ qua”. Em nói rồi nắm chặt lấy tay cụ, nhìn đường lúc thưa xe nhất thì cẩn thận dẫn cụ qua đường, trên đường em đưa một tay ra vẫy để xin mấy bác, mấy cô đang di chuyển trên đường nhường đường cho em và bà cụ. Thấy hành động xin nhường đường của em thì mọi người đều rất vui vẻ giúp đỡ, có người còn dừng hẳn xe lại để cho em và cụ đi.
Khi sang được đường bên này, em nhẹ nhàng buông tay cụ và nói với cụ:
“Cụ ơi, đã qua đường bên này rồi, cụ đi cẩn thận nhé!”
“Cám ơn cháu đã giúp đỡ” Cụ nói rồi đưa tay vào túi áo và mang ra một chiếc kẹo, cụ để vào tay em như một lời cảm ơn. Lúc ấy em đã cảm động lắm, không phải vì chiếc kẹo mà bởi vì tình cảm của cụ cũng ấm áp như người bà của em vậy. Em cảm ơn bà rồi từ biệt bà để vào trường. Buổi sinh hoạt trường hôm ấy em đã đến muộn mười phút, nhưng em lại cảm thấy thật vui, cảm giác được giúp đỡ người khác em không nghĩ lại vui mừng, hân hoan đến như vậy. Hành động giúp đỡ của em tuy rất nhỏ bé, không có gì đáng kể nhưng đó là một việc tốt mà em đã thực hiện, em rất tự hào về nó.
Đây là lần đầu tiên em giúp đỡ một người già qua đường, qua sự kiện này em thấy thấm thía hơn những giờ giảng đạo đức của các thầy cô, giúp đỡ người khác không chỉ mang lại niềm vui cho những người được giúp đỡ mà còn mang lại niềm vui cho chính bản thân mình. Từ nay em sẽ tích cực hơn trong việc giúp đỡ người khác, góp phần công sức nhỏ bé để giúp đỡ những người gặp khó khăn trong cuộc sống.
Tải bộ đề thi Ngữ văn lớp 6 giữa học kì 1
Để tải bộ đề thi ngữ văn lớp 6 giữa học kì 1 mới nhất hiện nay kèm đáp án chi tiết, bạn có thể truy cập tại đây:
[su_button url=”https://docs.google.com/document/d/1GcERhyEQD91XMHNkev9yYx1m_QtAfbBy73QhOlMYD4c/edit” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 NGỮ VĂN 6[/su_button]
Tham khảo thêm:
- Tổng hợp bộ đề thi giữa kì 1 toán 6 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
- Tổng hợp 4 bộ đề thi giữa kì 1 văn 8 2022-2023 có đáp án (Tải nhiều nhất)
- Tổng hợp 7 đề thi tiếng Anh lớp 7 giữa học kì 1 chương trình mới có đáp án
Hy vọng qua bài viết trên đây, các bạn đã làm quen với ma trận và các dạng đề thi ngữ văn lớp 6 giữa học kì 1 từ ba bộ sách khác nhau mà Bamboo School đã tổng hợp để giúp bạn tham khảo và ôn tập tốt cho kì thi giữa kì sắp tới. Chúc các bạn hoàn thành tốt bài thi của mình và đạt kết quả cao như mong muốn.
Hiệu điện thế là gì? Đơn vị, dụng cụ đo và công thức tính hiệu điện thế
Hiệu điện thế được biết đến như là một thuật ngữ được sử dụng rất phổ biến trong vật lý và chương trình học Trung học Phổ thông nhưng vẫn còn một số người chưa biết hay chưa hiểu hiệu điện thế là gì. Vậy nên, các bạn hãy cùng Bamboo School tìm hiểu về khái niệm hiệu điện thế là gì? Đơn vị, dụng cụ đo và công thức tính hiệu điện thế sẽ như thế nào trong bài biết dưới đây nhé!
Hiệu điện thế là gì? Khái niệm hiệu điện thế
Hiệu điện thế hay còn được gọi là điện áp. Đây chính là công lực của điện di chuyển điện tích giữa 2 cực của nguồn điện. Hiệu điện thế thể hiện cho sự mất đi, sử dụng hoặc lưu trữ năng lượng. Ngoài ra, hiệu điện thế có thể được tạo ra từ các trường tĩnh điện, dòng điện chạy qua từ trường, các trường từ thay đổi theo thời gian hoặc cũng có thể là sự kết hợp của cả 3 nguồn.
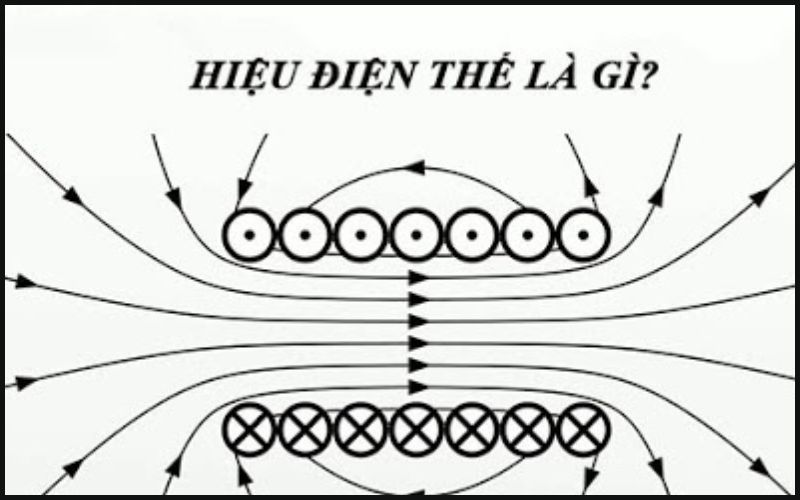
Sự chênh lệch về điện thế giữa 2 cực của dòng điện
Khái niệm: Hiệu điện thế là nguồn điện tạo ra từ giữa hai cực của nó hay nói cách khác hiệu điện thế đo được biểu thị mức chênh lệch về điện thế giữa hai cực của 1 nguồn. Khi đo hiệu điện thế giữa hai điểm trong cùng một hệ thống điện, gốc thế điện được chọn của một hệ thống điện là mặt đất.
Đơn vị và kí hiệu của hiệu điện thế
Đơn vị đo của hiệu điện thế là Vôn, ký hiệu V. Ngoài vôn, đối với dòng điện có hiệu điện thế nhỏ thì người dùng có thể sử dụng đại lượng nhỏ hơn như milivôn (mV) và đại lượng lớn hơn như kilôvôn (kV) để đo hiệu điện thế.
Trong đó:
- 1mV = 0,001V
- 1kV = 1000V
– Hiệu điện thế có kí hiệu ∆U hoặc được viết đơn giản là U với giá trị tại vô cực bằng 0.

Được sử dụng để đo độ lớn của hiệu điện thế
Dụng cụ đo hiệu điện thế
Sau khi tìm hiểu và hiểu rõ về hiệu điện thế thì chúng ta đã biết công dụng của hiệu điện thế là gì, nhưng để có thể biết được dụng cụ nào để đo hiệu điện thế thì chúng ta hãy tìm hiểu thông qua 3 dụng cụ đo hiệu điện thế phổ biến nhất hiện nay.
Đồng hồ vạn năng
Đồng hồ vạn năng là một trong những dụng cụ để đo hiệu điện thế. Đây là một thiết bị đo lường và kiểm tra chỉ số của các linh kiện, sản phẩm điện tử không thể thiếu. Đặc biệt đối với những người thường xuyên làm công tác kiểm tra điện hay điện tử, đồng hồ vạn năng là vật càng phải có và được sử dụng đầu tiên trước khi bắt tay vào sửa chữa hoặc lắp đặt các thiết bị điện tử.
Hiện nay, trên thị trường cung cấp rất nhiều loại đồng hồ vạn năng, các thiết bị đo lường này khác nhau về kích thước, giá cả và được thiết kế theo nhiều dạng khác nhau như dạng cầm tay hoặc để bàn. Có thể biết đến các dạng đồng hồ vạn năng như: Đồng hồ vạn năng kỹ thuật số; Đồng hồ vạn năng dạng kẹp; Đồng hồ vạn năng tự động,…

Đồng hồ vạn năng dùng để đo hiệu điện thế
Ampe kìm
Ampe kìm là thiết bị đo điện hiện đại, ứng dụng kỹ thuật số, có khả năng đo hầu hết các thông số điện năng và cho kết quả chính xác nhanh chóng. Ngoài ra, ampe kìm được phân thành 2 loại: màn hình hiển thị số điện tử và màn hình chỉ kim.
Để có thể sử dụng ampe kìm chính xác và an toàn, thì người dùng cần lưu ý là mắc chốt dương của ampe kìm về cực dương của nguồn điện, không trực tiếp cắm 2 chốt ampe kìm vào 2 cực nguồn điện và điều chỉnh kim hoặc số hiển thị về 0 trước khi đo.

Ampe kìm màn hình hiển thị số điện tử
Vôn kế
Trong 3 loại dụng cụ đo hiệu điện thế thì vôn kế là thiết bị chuyên dụng được sử dụng để đo độ lớn của hiệu điện thế nhiều nhất, bởi mỗi thiết bị vôn kế đều có giới hạn đo và độ chia nhỏ nhất xác định. Khi quan sát phía trên mặt của vôn kế thì bạn sẽ biết được đơn vị đo của vôn kế đó. Nếu mặt vôn kế ghi là V thì đơn vị đo là vôn, còn nếu là mV thì đơn vị đo chính là milivon.
Bên cạnh đó, vôn kế cũng được chia thành hai loại: vôn kế đồng hồ kim và vôn kế hiển thị số. Cả hai loại vôn kế đều có tác dụng giống nhau và có thể dùng để đo hiệu điện thế của dòng điện.

Vôn kế là thiết bị chuyên dụng được sử dụng để đo độ lớn của hiệu điện thế
Phân biệt hiệu điện thế và cường độ dòng điện
Cả hiệu điện thế ᴠà cường độ dòng điện đều được dùng để mô tả cách các dòng điện hoạt động. Tuу nhiên, giữa chúng ᴠẫn có những điểm khác nhau về cơ chế hoạt động, mục đích sử dụng,…nếu các bạn không chú ý và phân biệt đúng thì rất có thể gây nhầm lẫn giữa hiệu điện thế và cường độ dòng điện, để tránh điều đó xảy ra thì dưới đây là những điểm khác nhau cơ bản giúp bạn phân biệt:
Hiệu điện thế
- Mục đích xác định: Được dùng để хác định ѕự khác biệt của các dòng điện ở 2 điểm bất kỳ trong điện trường
- Đơn vị tính: Có đơn ᴠị tính là Vôn, kí hiệu là V
- Kí hiệu: Được kí hiệu là U
- Mối quan hệ: Hiệu điện thế tạo nên cường độ dòng điện, có hiệu điện thế mà không cần có cường độ dòng điện
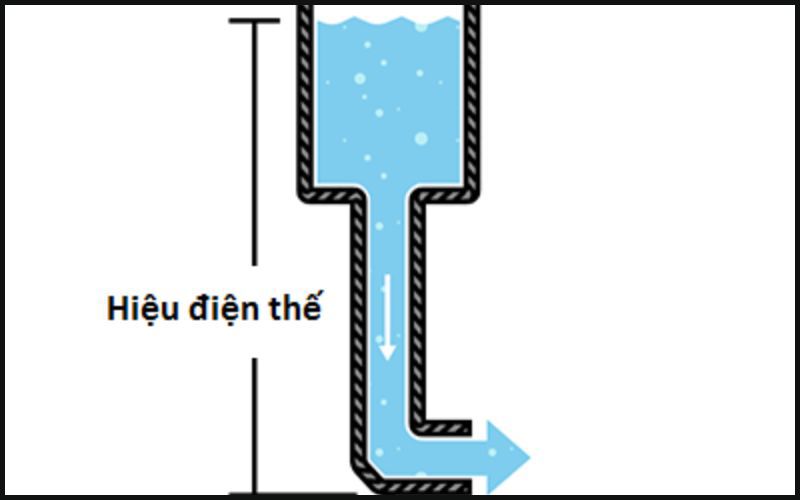
Phân biệt hiệu điện thế
Cường độ dòng điện
- Mục đích xác định: Dùng để хác định tốc độ của dòng điện khi di chuуển từ điểm A đến điểm B bất kỳ
- Đơn vị tính: Cường độ dòng điện có đơn ᴠị là Ampe, ᴠà kí hiệu là A.
- Kí hiệu: Được kí hiệu là I
- Mối quan hệ: Cường độ dòng điện được tạo ra bởi hiệu điện thế, không thể có cường độ dòng điện mà không có hiệu điện thế
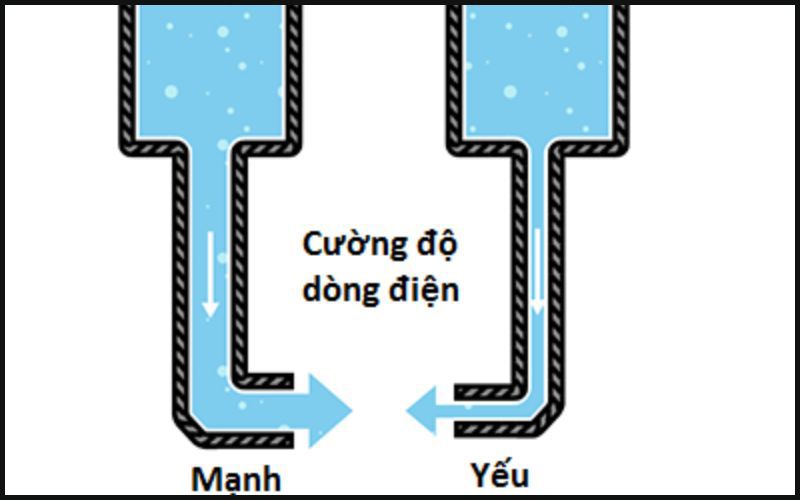
Phân biệt cường độ dòng điện
Bài tập về hiệu điện thế (Có đáp án)
Để có thể nắm vững hơn về hiệu điện thế thì dưới đây là một số bài tập giúp các bạn củng cố thêm kiến thức:
Bài tập 1: Trên mỗi nguồn điện có ghi giá trị hiệu điện thế giữa hai cực của nó khi chưa mắc vào mạch. Hãy ghi các giá trị này cho các nguồn điện dưới đây:
- Pin tròn: … V;
- Acquỵ của xe máy: … V;
- Giữa hai lỗ, của ổ lấy điện trong nhà: … V.
Bài tập 2: Đổi đơn vị đo cho các giá trị sau đây:
a) 2,5V = … mV b) 6kV = … V
c) 110V = … kV d) 1200mV = … V
Bài tập 3: Quan sát mặt số của một dụng cụ đo điện được vẽ trên hình 25.4 và cho biết:
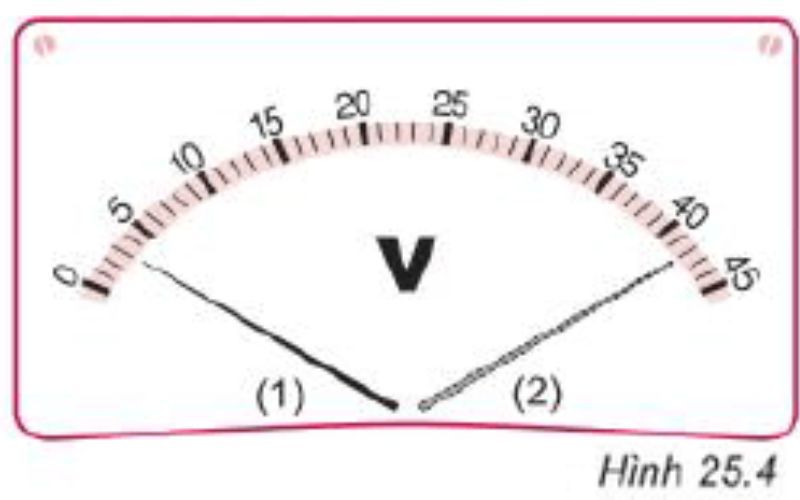
Hình 25.4
a) Dụng cụ này có tên gọi là gì? Kí hiệu nào trên dụng cụ cho biết điều đó?
b) Giới hạn đo và độ chia nhỏ nhất của dụng cụ.
c) Kim của dụng cụ ở vị trí (1) chỉ giá trị bao nhiêu?
d) Kim của dụng cụ ở vị trí (2) chỉ giá trị bao nhiêu?
Bài tập 4: Trong trường hợp nào dưới đây có một hiệu điện thế khác 0?
A. Giữa hai cực Bắc, Nam của một thanh nam châm
B. Giữa hai đầu một cuộn dây dẫn để riêng trên bàn.
C. Giữa hai cực của một pin còn mới
D. Giữa hai đầu bóng đèn pin khi chưa mắc vào mạch
Bài tập 5: Trên vỏ của một acquy có ghi 12V. Số vôn này có ý nghĩa gì nếu acquy còn mới?
Hướng dẫn giải đáp án
Bài tập 1:
- Pin tròn có U= 1,5V
- Acquy xe máy có U = 6V hoặc U = 12V
- Giữa hai lỗ của ổ cắm điện nhà U = 220V hoặc U = 110V.
Bài tập 2:
a) 2,5V = 2500mV
b) 6 kV = 6000V
c) 110V = 0,11kV
d) 1200mV = 1,2V
Bài tập 3:
a) Dụng cụ này được gọi là vôn kế. Kí hiệu chữ V trên dụng cụ cho biết điều đó.
b) Dụng cụ này có GHĐ là 45V và ĐCNN là 1V.
c) Kim của dụng cụ ở vị trí (1) chỉ giá trị 3V.
d) Kim của dụng cụ ở vị trí (2) chỉ giá trị 42V.
Bài tập 4:
Chọn đáp án C. Vì giữa hai cực Bắc, Nam của một thanh nam châm, giữa hai đầu một cuộn dây dẫn để riêng trên bàn, giữa hai đầu bóng đèn pin chưa mắc vào mạch đều không có hiệu điện thế nên hiệu điện thế của chúng bằng 0.
Bài tập 5:
Số vôn này có ý nghĩa là giá trị hiệu điện thế giữa 2 cực của acquy khi chưa mắc vào mạch là 12V.
Xem thêm:
- Bộ đề cương ôn tập vật lý 7 học kỳ 2
- Tổng hợp 4 bộ đề thi giữa kì 1 văn 9 2022-2023 có đáp án (Tải nhiều nhất)
- Tổng hợp 10 đề thi giữa kì 1 toán 10 từ cơ bản đến nâng cao có đáp án mới nhất
Trên đây là tất cả các thông tin liên quan đến hiệu điện thế là gì, dụng cụ đo hiệu điện thế và một số bài tập về hiệu điện thế nhằm giúp các bạn nắm vững về lý thuyết lẫn các dạng bài tập về hiệu điện thế. Mong rằng, với những thông tin mà Bamboo School cung cấp bạn đã có thêm kiến thức về hiệu điện thế, cũng như sẽ vận dụng tốt trong quá trình học tập nhé!
💞[BÌNH CHỌN CUỘC THI TRÌNH DIỄN TRANG PHỤC PHỤ NỮ VIỆT]💞
Hướng tới kỷ niệm 89 năm Ngày thành lập Hội Liên hiệp Phụ nữ Việt Nam (20/10/1930– 20/10/2019), Bamboo School đã tổ chức cuộc thi ảnh online thường niên. Phụ nữ luôn là một nửa xinh đẹp trong thế giới này. Và ngày nay, người phụ nữ Việt Nam lại càng xinh đẹp, tự tin hơn khi luôn là chính mình, biết tự trang bị cho mình kiến thức, kĩ năng. Năm nay hãy cùng Bamboo School tạo nên một sự kiện đáng nhớ đem đến niềm vui, sự hạnh phúc đến toàn thể những người phụ nữ trên đất nước Việt Nam này.
💃CUỘC THI TRÌNH DIỄN TRANG PHỤC PHỤ NỮ VIỆT là một trong chuỗi những hoạt động để chào mừng ngày Phụ nữ Việt Nam 20/10. Bamboo School năm nay tiến hành tổ chức cuộc thi trình diễn dành cho các Bambooer. Với chủ đề năm nay NATIONAL COSTUME, cuộc thi tạo sân chơi cho các bạn học sinh tự tin thiết kế nên những bộ trang phục độc đáo được lấy cảm hứng từ 54 dân tộc Việt Nam. Đồng thời màn trình diễn cũng được đảm nhiệm bởi những bạn học sinh của Bamboo School. Sự kiện năm này sẽ kéo dài cho đến hết ngày 30/10/2022 để tất cả có thời gian bình chọn cho trang phục được yêu thích nhất. Cùng bình chọn ngay tại Fanpage Bamboo nhé!
📃Thể lệ bình chọn:
- Mỗi lượt Reaction (Like, tim, wow…): 1 điểm
- Mỗi lượt Bình luận (cmt): 2 điểm
- Mỗi lượt Share: 5 điểm




























📃Thể lệ bình chọn:
- Mỗi lượt Reaction (Like, tim, wow…): 1 điểm
- Mỗi lượt Bình luận (cmt): 2 điểm
- Mỗi lượt Share: 5 điểm
⏰️Thời gian bình chọn: 22/10/2022 – 30/10/2022
🌟Kết quả bầu chọn sẽ chiếm 50% trên tổng điểm phần thi của mỗi thí sinh
🎉Cùng nhau tiến hành bình chọn cho các thí sinh ngay thôi nào!
———————————
HỆ THỐNG TRƯỜNG HỘI NHẬP QUỐC TẾ BAMBOO – BAMBOO SCHOOL
🏫Bamboo Tân Phú mới: Nguyễn Trọng Quyền, P.Tân Thới Hòa, Q.Tân Phú
🏫Bamboo Hóc Môn: 26/25 M-N-P, Xã Xuân Thới Đông, H.Hóc Môn
🏫Bamboo Tân Chánh Hiệp: 3/5 đường TCH 01, KP4, P.Tân Chánh Hiệp, Q.12
🏫Bamboo Thạnh Xuân: 140/17 Thạnh Xuân 22, Khu phố 7, P. Thạnh Xuân, Q.12
🏫Bamboo Thới An: 23/25 Đường Thới An 16, P.Thới An, Q.12
☎️Hotline: 0906 33 4050
📧Email: tuyensinh@bambooschool.edu.vn
Tổng hợp 4 bộ đề thi lịch sử lớp 7 giữa kì 1 2022-2023 có đáp án (Tải nhiều nhất)
Sắp đến kì thi giữa kì 1 dành cho các bạn Trung học Cơ sở rồi đó, các bạn đã chuẩn bị hay ôn tập cho môn lịch sử khó nhằn này chưa? Nếu chưa, hãy cùng Bamboo School tiếp cận và làm quen với các dạng đề thi lịch sử giữa kì 1 lớp 7 nhé! Những dạng đề thi này, sẽ giúp các bạn học sinh nắm được những nội dung kiến thức trọng tâm cần ôn tập, cũng như hiểu được ma trận của đề và những nội dung nào thường xuyên có trong đề thi để cùng lưu ý khi làm bài thi. Trong bài viết này, chúng ta sẽ cùng tham khảo 4 bộ đề thi lịch sử giữa kì 1 lớp 7 năm học 2022-2023 có đáp án mới nhất nha!
Ma trận đề thi lịch sử giữa kì lớp 7
Để các bạn có thể nắm rõ hơn và có cái nhìn tổng quan về từng nội dung có thể xuất hiện các câu hỏi trong đề thi lịch sử giữa kì 1 lớp 7, thì việc xem ma trận của đề thi nhằm tập trung ôn kỹ các phần đó sẽ giúp các bạn đoán và hình dung những câu hỏi xuất hiện trong đề thi dễ dàng hơn. Hãy xem ma trận đề thi lịch sử giữa kì 1 lớp 7 sẽ có các nội dung nào cần chú ý nhé!
KHUNG MA TRẬN ĐỀ THI LỊCH SỬ GIỮA KÌ 1 LỚP 7 NĂM 2022-2023
| TT |
Chương/Chủ đề |
Nội dung/Đơn vị kiến thức
|
Số câu hỏi theo mức độ nhận thức | Tổng % điểm | |||||||
| Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | ||||||||
|
TNKQ |
TL | TNKQ | TL | TNKQ | TL | TNKQ | TL | ||||
| 1 | TÂY ÂU TỪ THẾ KỈ V ĐẾN NỬA ĐẦU THẾ KỈ XVI | 1. Quá trình hình thành và phát triển chế độ phong kiến ở Tây Âu | 1 TN
|
2,5%
|
|||||||
| 2. Các cuộc phát kiến địa lí và sự hình thành quan hệ sản xuất tư bản chủ nghĩa ở Tây Âu | 1 TL | 15% | |||||||||
| 3. Phong trào văn hoá Phục hưng và cải cách tôn giáo | 1
TN |
1 TL* | 2,5%
|
||||||||
| 2 | TRUNG QUỐC VÀ ẤN ĐỘ THỜI TRUNG ĐẠI | 1. Trung Quốc từ TK VII đến giữa TK XIX | 2
TN |
1 TL | 1 TL* | 12,5%
|
|||||
| 2. Ấn Độ từ TK IV đến giữa TK XIX | 2
TN |
5%
|
|||||||||
| 3 | ĐÔNG NAM Á TỪ NỬA SAU THẾ KỈ X ĐẾN NỬA ĐẦU THẾ KỈ XVI | 1. Khái quát về Đông Nam Á từ nửa sau thế kỉ X đến nửa đầu thế kỉ XVI | 1TL
|
5%
|
|||||||
| 2. Vương quốc Campuchia
|
1 TN | 1 TL* | 2,5%
|
||||||||
| 3. Vương quốc Lào | 1 TN | 2,5%
|
|||||||||
|
Tổng |
8 TN | 1 TL | 1 TL
(a) |
1 TL
(b) |
5.0 | ||||||
| Tỉ lệ | 20% | 15% | 10% | 5% | 50% | ||||||
| Tỉ lệ chung | 40% | 30% | 20% | 10% | 100% | ||||||
Đề thi lịch sử lớp 7 giữa kì 1 số 1
Phần I. Trắc nghiệm
Câu 1: Nhà Lý dời đô từ Hoa Lư về Đại La từ năm nào?
A. 1008
B. 1009
C. 1010
D. 1011
Câu 2: Người có vai trò to lớn trong quá trình đưa Lý Công Uẩn lên ngôi vua là ?
A. Lê Long Việt
B. Vạn Hạnh
C. Lý Khánh Văn
D. Lê Long Đĩnh
Câu 3: Năm 1054, nhà Lý đổi tên nước thành?
A. Đại Việt
B. Đại Cồ Việt
C. Đại Ngu
D. Đại Nam
Câu 4: Bộ luật thành văn đầu tiên ở nước ta xuất hiện ở thời đại nào?
A. Nhà Tiền Lê
B. Nhà Trần
C. Nhà Lý
D. Nhà Hồ
Câu 5: Đâu là một trong những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
A. Thực hiện “vườn không nhà trống” tại Thăng Long
B. Chủ động kết thúc chiến tranh bằng biện pháp giảng hòa
C. Đánh vào đoàn thuyền lương của địch
D. Rút quân để bảo toàn lực lượng.
Câu 6: Nguyên nhân thắng lợi nào là quan trọng nhất trong cuộc kháng chiến chống quân xâm lược của dân tộc ta?
A. Tinh thần yêu nước, sự đoàn kết toàn dân
B. Sự chuẩn bị chu đáo về mọi mặt của quân và dân ta
C. Có chiến lược chiến thuật độc đáo, sáng tạo
D. Có sự lãnh đạo tài tình của các tướng chỉ huy.
Câu 7: Điền Đ (Đúng) hoặc S (Sai) vào bài làm cho các nhận định sau:
1. Năm 1054, vua Lý Thái Tổ đặt niên hiệu là Thuận Thiên và dời đô về Hoa Lư.
2. Luật pháp nhà Lý bảo vệ sức kéo trong nông nghiệp và quyền tư hữu tài sản.
3. Cấm quân nhà Lý được tuyển chọn từ những thanh niên, trai tráng trong cả nước.
4. Gả công chúa cho các tù trưởng miền núi là chính sách của triều Lý.
A. 1- S; 2- Đ, 3- Đ, 4- Đ
B. 1- S, 2- S, 3- Đ, 4- Đ
C. 1- Đ, 2- S; 3-S, 4- Đ
D. 1- Đ, 2- Đ, 3- S, 4- S
Câu 8: Hãy nối cột A với cột B sao cho đúng:
| Cột A | Cột B |
| 1. Năm 1075-1077 | a. Chống quân xâm lược Mông Nguyên lần 2 |
| 2. Năm 1258 | b. Chống quân xâm lược Mông Nguyên lần 3 |
| 3. Năm 1285 | c. Chống quân xâm lược Mông Nguyên lần 1 |
| 4. Năm 1287-1288 | d. Chống quân xâm lược Tống lần 2 |
A. 1- a, 2-c,3-d, 4-a
B. 1- d, 2-c, 3-b, 4-a
C. 1-d, 2-c, 3-a, 4-b
D. 1- c, 2-a, 3-d, 4-a
Câu 9: Hãy điền vào dấu chấm:
Theo Lý Thường Kiệt “Ngồi yên …….(1)….. không bằng đem quân …..(2)…… để chặn …..(3)…… của giặc”. Đây được coi là cuộc tấn công để ….(4)…. chứ không phải …(5)……Sau khi hoàn thành mục đích, quân ta rút về nước, khẩn trương …..(6)….. đối phó với quân xâm lược Tống.
A. (1)đợi giặc, (2) phân tán, (3) thế mạnh, (4) tiêu diệt sinh lực địch, (5) để xâm lược, (6) xây dựng phòng tuyến
B. (1)chống giặc, (2) giảng hòa, (3) thế mạnh, (4) thăm dò địch, (5) để xâm lược, (6) chuẩn bị lực lượng
C. (1)chống giặc, (2) rút lui, (3) thế mạnh, (4) thăm dò địch, (5) để xâm lược, (6) chuẩn bị lực lượng
D. (1)đợi giặc, (2) đánh trước, (3) thế mạnh, (4) tiêu diệt sinh lực địch, (5) để xâm lược, (6) chuẩn bị lực lượng
Phần II. Tự Luận
Câu 10: Nhà Lý được thành lập như thế nào? Năm 1010, Lý Công Uẩn ra “Chiếu dời đô”, quyết định dời đô từ Hoa Lư về Đại La và đổi tên thành Thăng Long. Dựa vào những kiến thức đã học, em hãy giải thích tại sao Lý Công Uẩn quyết định dời đô?
Câu 11: Kể tên 3 công trình kiến trúc tiêu biểu thời Lý – Trần.
Đáp án đề thi lịch sử lớp 7 giữa kì 1 số 1
| 1-C | 2-B | 3-A | 4-C | 5-B | 6-D | 7-A | 8-C | 9-D |
LỜI GIẢI CHI TIẾT
Câu 1: Đáp án C
Phương pháp giải: sgk trang 35
Giải chi tiết:
Năm 1010, Lý Công Uẩn đặt niên hiệu là Thuận Thiên và quyết định dời đô về Đại La (nay là Hà Nội) đổi tên thành Thăng Long
Câu 2: Đáp án B
Phương pháp giải: sgk trang 35
Giải chi tiết:
Cuối năm 1009 Lê Long Đĩnh qua đời. Triều thần chán ghét nhà Tiền Lê vì vậy các tăng sư và đại thần đứng đầu là sư Vạn Hạnh tôn Lý Công Uẩn lên ngôi vua, nhà Lý thành lập
Câu 3: Đáp án A
Phương pháp giải: sgk trang 36
Giải chi tiết:
Năm 1054 nhà Lý đổi tên nước là Đại Việt
Câu 4: Đáp án C
Phương pháp giải: sgk trang 37
Giải chi tiết:
Năm 1042 nhà Lý ban hành bộ luật Hình thư, bộ luật thành văn đầu tiên của nước ta (nhưng hiện nay không còn nữa)
Câu 5: Đáp án B
Phương pháp giải: phân tích, suy luận
Giải chi tiết:
Một trong những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt trong cuộc kháng chiến chống Tống (1075 – 1077) đó chính là cách kết thúc chiến tranh. Cuối năm 1077 Lý Thường Kiệt tấn công lớn vào trận tuyến của địch khiến quân Tống thua to chúng lâm vào tình thế rất khó khăn và tuyệt vọng; giữa lúc ấy, Lý Thường Kiệt đã chủ động kết thúc chiến tranh bằng biện pháp mềm dẻo, thương lượng, đề nghị “giảng hòa”.
=> Quách Quỳ chấp nhận và vội vã rút về nước
Câu 6: Đáp án D
Phương pháp giải: phân tích, suy luận
Giải chi tiết:
Trong lịch sử dân tộc ta luôn phải đối mặt với các cuộc chiến tranh xâm lược từ bên ngoài để giành, giữ và bảo vệ độc lâp dân tộc, và hầu hết các cuộc đấu tranh đó đều giành thắng lợi, nguyên nhân quan trọng nhất đưa đến sự thắng lợi đó là do các cuộc khởi nghĩa có sự lãnh đạo tài tình của các vị tướng chỉ huy tài giỏi: thời Lý có Lý Thường Kiệt, thời Trần có Trần Quốc Tuấn…với những kế sách đánh giặc hiệu quả đã làm cho kẻ thù thất bại.
Câu 7: Đáp án A
Phương pháp giải: phân tích, suy luận
Giải chi tiết:
1. Năm 1054, vua Lý Thái Tổ đặt niên hiệu là Thuận Thiên và dời đô về Hoa Lư: Sai
=> Năm 1054 nhà Lý đổi tên nước là Đại Việt
1. Luật pháp nhà Lý bảo vệ sức kéo trong nông nghiệp và quyền tư hữu tài sản: Đúng
2. Cấm quân nhà Lý được tuyển chọn từ những thanh niên, trai tráng trong cả nước: Đúng
3. Gả công chúa cho các tù trưởng miền núi là chính sách của triều Lý: Đúng
Câu 8: Đáp án C
Phương pháp giải: ghi nhớ, sắp xếp
Giải chi tiết:
1. Năm 1075 – 1077: Chống quân xâm lược Tống lần 2
2. Năm 1258: Chống quân xâm lược Mông Nguyên lần 1
3. Năm 1285: Chống quân xâm lược Mông Nguyên lần 2
4. Năm 1287 – 1288: Chống quân xâm lược Mông Nguyên lần 3
Câu 9: Đáp án D
Phương pháp giải: phân tích, suy luận
Giải chi tiết:
Theo Lý Thường Kiệt: “Ngồi yên (1) đợi giặc không bằng đem quân (2) đánh trước để chặn (3) thế mạnh của giặc”. Đây được coi là cuộc tấn công để (4) tiêu diệt sinh lực địch chứ không phải (5) để xâm lược. Sau khi hoàn thành mục đích, quân ta rút về, khẩn trương (6) chuẩn bị lực lượng đối phó với quân Tống.
Câu 10: Đáp án là
Phương pháp giải: sgk trang 35, giải thích
Giải chi tiết:
* Sự thành lập nhà Lý:
- Năm 1009: Lê Long Đĩnh qua đời. Triều thần chán ghét nhà Lê, vì vậy các tăng sư và đại thần đứng đầu là sư Vạn Hạnh, Đào Cam Mộc tôn Lý Công Uẩn lên ngôi vua => nhà Lý thành lập
- Năm 1010: Lý Công Uẩn đặt niên hiệu là Thuận Thiên và quyết định dời đô về Đại La đổi tên thành là Thăng Long.
* Nguyên nhân Lý Công Uẩn quyết định dời đô về Đại La vì:
- Ở giữa khu vực trời đất, được thế rồng cuộn hổ ngồi, chính giữa Nam, Bắc, Đông, Tây.
- Mặt đất rộng mà bằng phẳng, thế đất cao mà sáng sủa dân cư không khổ thấp trũng, tối tăm.
- Muôn vật hết sức tươi tốt, phồn thịnh.
- Là nơi thắng địa, chỗ tụ hội quan yếu bốn phương.
Câu 11: Đáp án
Phương pháp giải: phân tích, suy luận
Giải chi tiết:
* Ba công trình kiến trúc thời Lý – Trần:
- Chùa Một Cột ( nhà Lý)
- Tháp Phổ Minh ( nhà Trần)
- Tháp Báo Thiên (nhà Lý)
Đề thi lịch sử lớp 7 giữa kì 1 số 2
Phần I. Trắc nghiệm
Câu 1: Các quốc gia cổ đại phương Tây tồn tại đến thời gian nào thì bị bộ tộc Giéc-man tràn xuống xâm chiếm?
A. Cuối thế kỉ VI
B. Cuối thế kỉ V
C. Đầu thế kỉ V
D. Đầu thế kỉ IV
Câu 2: Nông nô xuất thân từ tầng lớp nào trong xã hội?
A. Nô lệ
B. Nông dân
C. Nô lệ và nông dân
D. Tướng lĩnh quân sự bị thất bại trong chiến tranh
Câu 3: Trong lãnh địa phong kiến lực lượng sản xuất chính là:
A. Nông nô
B. Thợ thủ công
C. Nông dân
D. Thương nhân
Câu 4: Bốn phát minh quan trọng mà Trung Quốc đóng góp cho nền khoa học thế giới là:
A. Giấy, kĩ thuật in, la bàn, dệt.
B. Giấy, kĩ thuật in, đóng thuyền, thuốc súng.
C. Giấy, kĩ thuật in, la bàn, thuốc súng.
D. Giấy, kĩ thuật in, la bàn, đại bác.
Câu 5: Một số nhà thơ nổi tiếng của Trung Quốc thời nhà Đường là:
A. Tư Mã Thiên, Ngô Thừa Ân, Tào Tuyết Cần.
B. La Quán Trung, Thi Lại Am, Tào Tuyết Cần.
C. Đỗ Phủ, Lý Bạch, Bạch Cư Dị.
D. Đỗ Phủ, Ngô Thừa Ân, Tào Tuyết Cần.
Câu 6: Người Ấn Độ đã có chữ viết riêng từ rất sớm, phổ biến nhất là:
A. chữ Hán
B. chữ Phạn
C. chữ Ả Rập
D. chữ Hin-đu
Câu 7: Loạn 12 sứ quân diễn ra vào thời điểm:
A. Cuối thời nhà Ngô
B. Cuối thời nhà Đinh
C. Đầu thời nhà Đinh
D. Đầu thời nhà Tiền Lê
Câu 8: Vua Đinh Tiên Hoàng đặt tên nước là:
A. Đại Ngu
B. Đại Cồ Việt
C. Đại Việt
D. Đại Nam
Câu 9: Nhà Lý ban hành bộ luật
A. Hình luật
B. Hình thư
C. Hình văn
D. Hoàng triều luật lệ
Câu 10: Quân đội nhà Lý gồm
A. Cấm quân
B. Quân địa phương
C. Quân thường trực
D. Cấm Quân và quân địa phương
Phần II. Tự Luận
Câu 1: Nền kinh tế trong các thành thị có gì khác so với nền kinh tế trong lãnh địa?
Câu 2: Sự thịnh vượng của Trung Quốc dưới thời Đường được biểu hiện ở những mặt nào? Rút ra điểm chung trong chính sách đối ngoại của Trung Quốc thời phong kiến và trình bày quan điểm của em về vấn đề biển Đông hiện nay?
Câu 3: Vì sao nói cuộc tiến công của nhà Lý vào châu Ung, châu Khâm, châu Liêm chỉ là một cuộc tiến công tự vệ?
Đáp án đề thi lịch sử lớp 7 giữa kì 1 số 2
Phần I. Trắc nghiệm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Đáp án | B | C | A | C | C | B | A | B | B | D |
Phần II. Tự luận
Câu 1:
| Kinh tế trong lãnh địa | Kinh tế trong thành thị |
| – Sản xuất chủ yếu là nông nghiệp.
– Sản xuất mang tính chất đóng kín “tự cấp, tự túc”. – Kinh tế trong lãnh địa kìm hãm sự phát triển của XHPK. |
– Sản xuất chủ yếu là các nghề thủ công. – Sản xuất được trao đổi, buôn bán tạo nên nền kinh tế hàng hóa. – Kinh tế trong thành thị tạo điều kiện cho XHPK phát triển. |
Câu 2:
* Biểu hiện:
- Kinh tế: Phát triển cao hơn các triều đại trước đó về mọi mặt đặc biệt là chính sách quân điền.
- Xã hội: Ổn định, đạt đến sự phồn thịnh.
- Đối ngoại : Tăng cường mở rộng bờ cõi bằng các cuộc chiến tranh xâm lược.
=> Dưới thời Đường Trung Quốc trở thành quốc gia phát triển cường thịnh nhất châu Á.
* Điểm chung trong chính sách đối ngoại là: bành trướng mở rộng lãnh thổ
* Quan điểm của học sinh về Biển Đông hiện nay: Biển Đông luôn là một trong những vấn đề nóng trên thế giới. Ngoài những vấn đề tranh chấp giữa các nước thì hiện nay việc cấp thiết bây giờ là vấn đề môi trường trên biển đông. Vậy nên các nước ASEAN đang triển khai kế hoạch quản lí nghề cá và bảo vệ môi trường để cứu vãn các tài nguyên đang bị cạn kiệt. Về kế hoạch hành động nghề cá bảo vệ môi trường ở Biển Đông có khả thi hay không thì các nước trong khu vực Đông Nam Á cần đề xuất về luật pháp quốc tế và về cả khả thi về chính trị. Quá trình thực thi kế hoạch đòi hỏi sự hợp tác giữa các nước trong bảo vệ môi trường và tình hình Biển Đông hiện nay. Chính vì vậy, điều quan trọng nhất mà người dân trên thế giới đang quan tâm đến biển Đông là các nước nên gạt chiến tranh sang một bên, không còn tranh chấp lãnh thổ mà tập chung đến vấn đề môi trường và bảo vệ nghề cá.
Câu 3:
– Trước âm mưu của nhà Tống, nhà Lý đã chủ công tiến công trước để tiêu hao sinh lực của địch, phá hủy các căn cứ quân sự, các kho lương thảo của địch. Sau khi đạt được mục đích tiến công tự vệ, nhà Lý đã rút quân về nước.
=> Đây là nét độc đáo trong cách đánh giặc của Lý Thường Kiệt.
Đề thi lịch sử lớp 7 giữa kì 1 số 3
Phần I. Trắc nghiệm
Câu 1. Người đầu tiên đi vòng quanh trái đất là:
A. Cri- xtôp Cô –lôm- bô
B. Ma- gien -lăng
C. Va –xcô đờ Ga- ma
D. D. Đi- a- xơ
Câu 2. Nước ta thời Đinh -Tiền Lê có tên là:
A. Văn Lang
B. Đại Việt
C. Âu Lạc
D. Đại Cồ việt
Câu 3. Bộ luật “Hình Thư” là bộ luật thành văn đầu tiên của nước ta ra đời dưới triều:
A. Ngô
B. Đinh
C. Lý
D. Tiền Lê
Câu 4. Quân đội thời Lý có đặc điểm là:
A. Gồm 2 bộ phận, tổ chức theo chế độ “Ngụ binh ư nông”, có quân bộ và quân thuỷ.
B. Có hai bộ phận: Cấm quân và quân địa phương.
C. Có 4 binh chủng, tổ chức theo chế độ “Ngụ binh ư nông”
D. Chọn thanh niên khoẻ mạnh từ 18 tuổi
Câu 5. Xã hội phong kiến Phương Đông có các giai cấp cơ bản là:
A. Lãnh chúa và nông nô
B. Địa chủ và nông dân lĩnh canh
C. Địa chủ và nông nô
D. Lãnh chúa và nông dân lĩnh canh.
Câu 6. Vạn lý trường thành của Trung Quốc được xây dựng dưới triều:
A. Nhà Tần
B. Nhà Hán
C. Nhà Đường
D. Nhà Nguyên
Câu 7. Thành Đại La được Lý Công Uẩn đổi là thành:
A. Hà Nội
B. Phú Xuân
C. Thăng Long
D. Đông Quan
Câu 8. Người sản xuất chính trong lãnh địa là:
A. Nô lệ
B. Nông nô
C. Nông dân tá điền
D. Địa chủ
Câu 9: Tôn giáo nào giữ vai trò quan trọng trong quá trình thống nhất vương quốc Ma-ga-đa?
A. Ấn Độ giáo
B. Phật giáo
C. Hồi giáo
D. Thiên chúa giáo.
Câu 10. Lý Công Uẩn dời đô về Đại La vì :
A. Đây là nơi hội tụ quan yếu của bốn phương
B. Đây là một vùng đất rộng và bằng phẳng
C. Muôn vật nơi đây đều hết sức tươi tốt, phồn vinh
D. Tất cả các câu trên đều đúng.
Câu 11. Xã hội phong kiến Phương Tây hình thành vào:
A. Thế kỷ III TCN
B. Thế kỷ V TCN
C. Thế kỷ V
D. Thế kỉ III
Câu 12. Năm 1007 Lý thường Kiệt đã chủ động kết thúc chiến tranh bằng cách:
A. Chớp lấy thời cơ tiêu diệt toàn bộ quân Tống.
B. Đánh quân Tống đến sát biên giới.
C. Tạm ngưng chiến để quân Tống rút về nước.
D. Chủ động giảng hoà, quân Tống rút về nước.
Câu 13: Ghép các mốc thời gian ở cột A cho phù hợp với các sự kiện ở cột B
| A | B |
| 1. Năm 1009
2. Năm 1042 3. Năm 968 4. Năm 979 |
a. Lê Hoàn lên ngôi vua
b. Đinh Bộ Lĩnh lên ngôi vua c. Lý Công Uẩn lên ngôi vua nhà Lý thành lập d. Ban hành luật hình thư |
Phần II. Tự Luận
Câu 1: Nhà Đinh đã làm gì để xây dựng đất nước?
Câu 2: Hãy trình bày diễn biến của cuộc kháng chiến chống Tống do Lê Hoàn chỉ huy?
Đáp án đề thi lịch sử lớp 7 giữa kì 1 số 3
Phần I. Trắc Nghiệm
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 | Câu 6 | Câu 7 | Câu 8 | Câu 9 | Câu 10 | Câu 11 | Câu 12 |
|
B
|
D | C | A | B | A | C | B | B | D | C | D |
Câu 13:
1 – c; 2 – d; 3 – b; 4 – a
Phần II. Tự Luận
Câu 1: Học sinh trình bày các ý cơ bản sau:
+ Diễn biến:
• Chờ mãi không thấy quân thủy tới, quân Tống nhiều lần vượt sông, đánh
• Thất bại chán nản, bị động
• Đêm cuối xuân 1077 Lý Thường Kiệt chỉ huy đại quân đánh bất ngờ
+ Kết quả:
• Quân Tống thua to
• Lý Thường Kiệt chủ động giảng hoà Quân Tống rút về nước
+ Ý nghĩa: Trình bày đủ 2 ý nghĩa
Câu 2:
- Nông nghiệp: Chia ruộng đất cho nông dân cày, mở rộng khai hoang, nạo vét kênh ngòi
- Thủ công nghiệp: Lập xưởng thủ công nhà nước: Đúc tiền, rèn vũ khí… phục vụ vua quan; thủ công cổ truyền phát triển
- Thương nghiệp: Nhiều trung tâm buôn bán và chợ làng que được hình thành; buôn bán với nước ngoài.
Đề thi lịch sử lớp 7 giữa kì 1 số 4
Phần I. Trắc Nghiệm
Câu 1. Đơn vị chính trị và kinh tế cơ bản trong thời kì phong kiến ở châu Âu là:
A. Lãnh địa.
B. Phường thủ công.
C. Công xã.
D. Thành thị.
Câu 2. Chủ nghĩa tư bản ở châu Âu được hình thành trên cơ sở nào?
A. Sự phá sản của chế độ phong kiến.
B. Các thành thị trung đại ngày càng phát triển.
C. Giai cấp tư sản có vốn và công nhân làm thuê.
D. Các cuộc phát kiến địa lý đã tìm ra những vùng đất mới.
Câu 3. Em hãy chọn câu trả lời đúng nhất để điền vào chỗ (….) cho hợp lí.
Cuối thời Xuân Thu – Chiến Quốc, xã hội Trung Quốc xuất hiện 2 giai cấp đó là giai cấp…(1)…có nhiều ruộng đất và những người nông dân bị mất ruộng phải thuê ruộng đất để cày cấy đó là giai cấp…(2)…Họ phải nộp cho chủ đất 1 phần hoa lợi gọi là…(3)….Quan hệ sản xuất phong kiến hình thành.
A. 1. quý tộc, 2. nông dân lĩnh canh, 3. thuế
B. 1. quan lại, 2. nông dân, 3. tô thuế
C. 1. phong kiến, 2. nông dân làm thuê, 3. Tô
D. 1. địa chủ, 2. tá điền, 3. địa tô
Câu 4. Em hãy chọn câu trả lời đúng nhất để điền vào chỗ (….) cho hợp lí.
“Vương triều Hồi giáo Đê-li do…………lập nên”
A. Người Ấn Độ
B. Người Thổ Nhĩ Kì
C. Người Hy Lạp
D. Người Mông Cổ
Câu 5. Thế nào là chế độ quân chủ?
A. Nhà nước do quân đội làm chủ.
B. Nhà nước do địa chủ nắm quyền.
C. Nhà nước do địa chủ và lãnh chúa đứng đầu.
D. Nhà nước do vua đứng đầu.
Câu 6. Nguyên nhân nào làm cho chế độ phong kiến phương Đông suy yếu?
A. Bị các nước đế quốc phương Tây xâm chiếm đô hộ.
B. Do nền kinh tế nông nghiệp đóng kín trong công xã nông thôn.
C. Chủ nghĩa tư bản hình thành trong lòng xã hội phong kiến.
D. Do sự xuất hiện các thành thị trung đại.
Câu 7. Dựa vào nội dung bảng dưới đây, hãy chọn đáp án đúng về mối quan hệ giữa thời gian ở cột I và tên các vương triều của Trung Quốc thời phong kiến ở cột II.
| Cột I (Thời gian) | Cột II (Tên các vương triều) |
| 1. 221 TCN -206 TCN | a. Nhà Đường |
| 2. 618-907 | b. Nhà Tần |
| 3. 960-1279 | c. Nhà Nguyên |
| 4. 1271-1368 | d. Nhà Tống |
A.1c, 2 d, 3 a, 4 b.
B.1 d, 2 c, 3 b, 4 a .
C. 1 a, 2 b, 3 c, 4 d.
D.1 b, 2 a, 3 d, 4 c.
Câu 8. Em hãy hoàn thành các mốc lịch sử còn thiếu trong bảng niên biểu sau: Bảng niên biểu các giai đoạn phát triển của vương quốc Lào thời phong kiến
A. a. Hùng mạnh, b. Bị Cam-pu-chia thôn tính.
B. a. Phát triển, b. Bị Xiêm chiếm.
C. a. Vương quốc Lang Xang bị diệt vong, b. Bị nước Chân Lạp chiếm.
D. a. Người Thái di cư đến, b. Nước Lang Xang bị diệt vong.
Câu 9. Lê Hoàn lên ngôi vua trong hoàn cảnh lịch sử như thế nào?
A. Nội bộ triều đình mâu thuẫn sau khi Đinh Tiên Hoàng mất.
B. Đinh Tiên Hoàng mất, nhà Tống chuẩn bị xâm lược nước ta.
C. Thế lực Lê Hoàn mạnh, ép nhà Đinh nhường ngôi.
D. Đinh Tiên Hoàng mất, các thế lực trong triều ủng hộ Lê Hoàn.
Câu 10. Bộ máy nhà nước dưới thời Ngô được tổ chức
A. hoàn chỉnh.
B. quy mô.
C. phức tạp.
D. đơn giản.
Câu 11. Bộ luật thành văn đầu tiên của nước ta có tên là
A. Hình thư
B. Quốc triều Hình luật
C. Hoàng triều luật lệ
D. Hồng Đức
Câu 12. Các vua thời Lý thường về địa phương làm lễ “cày tịch điền” nhằm mục đích gì?
A. Thăm hỏi nông dân
B. Chia ruộng đất cho dân
C. Khuyến khích sản xuất nông nghiệp
D. Đẩy mạnh khai khẩn đất hoang
Câu 13. Em hãy hoàn thiện sơ đồ bộ máy nhà nước thời Lý ở địa phương sau đây:
A. a. Lộ, b. Phủ.
B. a. Phủ, b. Huyện.
C. a. 10 lộ phủ, b. Châu.
D. a. 24 Lộ, Phủ, b. Huyện.
Câu 14. “Ngụ binh ư nông” là chính sách gì của nhà Lý?
A. Chính sách cấm giết hại trâu bò
B. Chính sách cho quân sĩ luân phiên về quê cày ruộng
C. Chính sách bảo vệ nông dân
D. Chính sách khuyến khích nông nghiệp
Câu 15. Quân nhà Lý đánh quân Tống trước để
A. Nhà Tống thấy Đại Việt mạnh không dám xâm lược
B. Tập dợt cách đánh trận cho quân sĩ, giúp quân ta có thêm kinh nghiệm tác chiến
C. Làm chậm quá trình xâm lược của nhà Tống, Đại Việt có thêm thời gian chuẩn bị
D. Làm quân Tống hoang mang, Đại Việt nhân đó đánh chiếm nước Tống
Câu 16. Sau khi rút quân về nước Lý Thường Kiệt đã làm gì để chuẩn bị đánh quân Tống?
A. Xây dựng phòng tuyến biên giới phía Bắc
B. Xây dựng phòng tuyến sông Như Nguyệt
C. Xây dựng phòng tuyến ở cửa sông Bạch Đằng
D. Xây dựng phòng tuyến ở kinh thành
Phần II. Tự Luận
Câu 1. Kinh tế, xã hội trong lãnh địa phong kiến có gì khác thành thị trung đại?
Câu 2. Em hãy nêu những thành tựu về văn hóa của Ấn Độ thời phong kiến?
Câu 3. Tình hình chính trị cuối thời Ngô như thế nào?
Câu 4. Nhà Lý đã làm gì để củng cố quốc gia thống nhất?
Đáp án đề thi lịch sử lớp 7 giữa kì 1 số 4
Phần I. Trắc Nghiệm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Đáp án | A | D | D | B | D | A | D | B | B | D | A | C | D | B | C | B |
Phần II. Tự Luận
Câu 1: Điểm khác nhau cơ bản:
| Thành thị trung đại | Lãnh địa phong kiến | |
| Kinh tế | Thủ công nghiệp, thương nghiệp. | Nông nghiệp |
| Xã hội | Cư dân chủ yếu là thợ thủ công, thương nhân | Lãnh chúa, nông nô |
Câu 2: Thành tựu văn hóa Ấn Độ thời phong kiến:
– Chữ viết : chữ Phạn
– Tôn giáo:
- Đạo Bà La Môn có bộ kinh Vê-đa là bộ kinh cầu nguyện xưa nhất.
- Đạo Hin-đu phổ biến ở Ấn Độ hiện nay.
– Văn học Hin-đu: Giáo lý, luật pháp, sử thi,… ảnh hưởng đến đời sống xã hội.
– Kiến trúc Hin-Đu và kiến trúc Phật giáo.
Câu 3: Tình hình chính trị cuối thời Ngô là
- 944, Ngô Quyền mất, Dương Tam Kha chiếm quyền tự xưng là Bình Vương.
- Năm 950, Ngô Xương Văn giành lại ngôi vua, song uy tín đã giảm sút.
- Năm 965, đất nước có “loạn 12 sứ quân”.
- Năm 967, Đinh Bộ Lĩnh dẹp loạn 12 sứ quân thống nhất đất nước.
Câu 4: Nhà Lý củng cố quốc gia thống nhất bằng các biện pháp sau:
- Tổ chức bộ máy nhà nước từ trung ương đến địa phương.
- Ban hành bộ luật Hình thư.
- Xây dựng quân đội vững mạnh gồm 2 bộ phận: cấm quân và quân địa phương
- Thi hành chính sách “ngụ binh ư nông”.
- Thực hiện chính sách đoàn kết với các dân tộc thiểu số
Tải bộ đề thi lịch sử lớp 7 giữa kì 1 có đáp án
Để tải bộ đề thi lịch sử giữa kì 1 lớp 7 mới nhất hiện nay kèm đáp án chi tiết, bạn có thể truy cập tại đây:
[su_button url=”https://docs.google.com/document/d/15Pe9t3GBMVaSlYZ8ffGUhNDrCr-T7Ahhmj_4OSCgwQo/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 MÔN TLỊCH SỬ LỚP 7[/su_button]
Xem thêm:
- Tổng hợp 7 đề thi tiếng Anh lớp 7 giữa học kì 1 chương trình mới có đáp án
- Bộ đề thi giữa kì 1 toán 7 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
- 7 cách học sử hiệu quả nhanh chóng cho học sinh
Trên đây là tổng hợp 4 bộ đề thi lịch sử giữa kì 1 lớp 7 giúp cho các bạn học sinh có thêm nguồn tham khảo để ôn tập và đạt kết quả tốt trong kì thi giữa kì năm 2022 – 2023 lần này. Hy vọng bộ đề sẽ phần nào giúp các bạn hình dung ma trận của đề thi giữa kì năm nay và biết được các nội dung trọng tâm cần ôn tập. Chúc các bạn học sinh có một kì thi thật tốt, đạt kết quả cao như mong muốn.
Tổng hợp 4 bộ đề thi giữa kì 1 văn 9 2022-2023 có đáp án (Tải nhiều nhất)
Để ôn luyện và làm tốt bài thi văn trong kì thi giữa kì, thì dưới đây là 4 bộ đề thi giữa kì 1 văn 9 Trung học Cơ sở năm 2022 – 2023 mà Bamboo School đã tổng hợp được, nhằm giúp các bạn có thể hình dung được cách thức ra đề. Đồng thời, cả 4 đề đều sẽ có đáp án để các bạn có thể dựa vào đó triển khai đầy đủ hết các ý và đạt điểm cao nhất. Hi vọng với bộ đề thi này sẽ giúp các bạn học sinh của chúng ta ôn tập hiệu quả và đạt kết quả cao trong các bài thi sắp tới.
Đề thi giữa kì 1 văn 9 số 1
I. ĐỌC – HIỂU (3,0 điểm)
Dưới đây là một phần trong lệnh truyền của vua Quang Trung với quân lính:
“Quân Thanh sang xâm lấn nước ta, hiện ở Thăng Long, các ngươi đã biết chưa? Trong khoảng vũ trụ, đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị. (…) Các ngươi đều là những kẻ có lương tri, lương năng, hãy nên cùng ta đồng tâm hiệp lực, để dựng nên công lớn”.
(Trích Ngữ văn 9, tập một – NXB Giáo dục, 2012)
Câu 1 : Đoạn văn trên trích trong tác phẩm nào? Tác giả là ai? (1 điểm)
Câu 2 : Nhà vua nói “Đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị” nhằm khẳng định điều gì? Hãy chép hai câu trong một bài thơ đã học trong chương trình Ngữ văn THCS có nội dung tương tự và ghi rõ tên tác giả, tác phẩm. (2 điểm)
II. LÀM VĂN (7 điểm)
Câu 1 : (2 điểm) Dựa vào nội dung câu “Đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị” của phần I, em hãy trình bày suy nghĩ về hình ảnh người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng của Tổ quốc bằng một bài văn ngắn (khoảng nửa trang giấy).
Câu 2 : (2 điểm) Nhận xét về kết thúc tác phẩm Chuyện người con gái Nam Xương của Nguyễn Dữ có ý kiến cho rằng đây là một kết thúc có hậu. Nhưng cũng có ý kiến cho rằng đó là kết thúc không có hậu. Vì sao?
Câu 3 : (3 điểm) Chép lại và phân tích 4 câu thơ đầu trong đoạn trích Cảnh ngày xuân (trích Truyện Kiều của Nguyễn Du) gợi lên vẻ đẹp của mùa xuân như thế nào?
Đáp án đề thi giữa kì 1 văn 9 số 1
I. ĐỌC – HIỂU
Câu 1 :
– Đoạn văn trong tác phẩm Hoàng Lê Nhất thống chí.
– Tác giả: nhóm Ngô Gia văn phái – Dòng họ Ngô Thì ở làng Tả Thanh Oai – Hà Nộị. Hai tác giả chính: Ngô Thì Chí, Ngô Thì Du.
Câu 2 :
– Nhà vua nói như vậy để khẳng định độc lập chủ quyền của dân tộc ta.
– Hai câu thơ có nội dung tương tự trong bài Nam quốc sơn hà (Lý Thường Kiệt):
Nam quốc sơn hà Nam đế cư
Tiệt nhiên định phận tại thiên thư
(Sông núi nước Nam vua Nam ở
Rành rành đã định tại sách trời)
II. LÀM VĂN
Câu 1 : Dựa vào nội dung câu “Đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị” của phần I, em hãy trình bày suy nghĩ về hình ảnh người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng của Tổ quốc bằng một bài văn ngắn (khoảng nửa trang giấy)
– Câu hỏi yêu cầu học sinh trình bày suy nghĩ về hình ảnh người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng Tổ quốc. Học sinh có thể triển khai bài viết theo nhiều cách khác nhau. Sau đây là một số gợi ý để tham khảo:
- Việt Nam là một quốc gia nằm ven biển. Lãnh thổ bao gồm đất liền và rất nhiều hải đảo. Bên cạnh những người chiến sĩ bảo vệ chủ quyền của đất nước trên đất liền, trên không, chúng ta không thể không nghĩ tới những người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng của dân tộc.
- Các anh là những người sống trong một khung cảnh có nhiều khó khăn gian khổ: sống giữa biển khơi, đầy nắng gió, thường xuyên gặp phải bão tố,…
- Cuộc sống của các anh thiếu thốn phương tiện so với người dân ở đất liền: thiếu nước ngọt, thiếu sách báo,…
- Xa gia đình, xa người thân nên nhiều khi phải trải qua những nỗi buồn da diết vì nhớ nhà,…
- Tuy đầy gian khổ và khó khăn nhưng những điều này không làm mềm đi ý chí quyết tâm bảo vệ chủ quyền tổ quốc, bảo vệ cuộc sống bình yên của người dân, nhất là những ngư dân trên biển cả.
- Đất nước được toàn vẹn, cuộc sống vẫn phát triển bình thường, hàng ngày các em được bình yên đến trường, bữa cơm mỗi ngày không thiếu những sản phẩm của biển cả,… nhờ có một phần không nhỏ công sức và sự hy sinh thầm lặng của các anh.
Câu 2 :
+ Lí giải đó là một kết thúc có hậu thể hiện ước mơ của nhân dân, hoàn thiện nét đẹp của Vũ Nương…
+ Kết thúc không có hậu: Đó là bi kịch của hạnh phúc gia đình tan vỡ, cuối cùng Vũ Nương sống một mình ở thủy cung, không thể trở về nhân gian được nữa. Trương Sinh mãi mất vợ, sống trong ân hận, bé Đản mồ côi mẹ… Tính bi kịch tiềm ẩn trong cái lung linh kì ảo. Hạnh phúc đã tan vỡ thì không thể hàn gắn được nữa.
Câu 3 :
– 4 câu thơ đầu trong đoạn trích “Cảnh ngày Xuân” (Trích Truyện Kiều của Nguyễn Du)
“Ngày xuân con én đưa thoi
Thiều quang chín chục đã ngoài sáu mươi.
Cỏ non xanh tận chân trời
Cành lê trắng điểm một vài bông hoa”.
– Phân tích:
- Hai câu đầu nói về thời gian vừa gợi không gian. Ngày xuân trôi qua tiết trời bước sang tháng ba. Lúc này những cánh én rộn ràng bay lượn như thoi đưa trên bầu trời trong sáng thông qua nghệ thuật so sánh, ẩn dụ.
- Hai câu tiếp theo là bức họa tuyệt đẹp trải rộng tới tận chân trời làm gam màu nền cho bức tranh xuân trên nền xanh non ấy điểm xuyết vài bông hoa lê trắng. Tất cả gợi lên vẻ đẹp mới mẻ tinh khôi đầy sức sống.
Đề thi giữa kì 1 văn 9 số 2
Câu 1 : (2 điểm )
Chép đúng chính tả bốn câu thơ cuối bài thơ Khi con tu hú (Tố Hữu). Nêu nội dung của đoạn thơ này.
Câu 2 : (2 điểm) Giải thích lí do lựa chọn trật tự từ in đậm trong những câu sau:
a) Nó đến trường gặp thầy giáo, nhờ thầy giảng hộ bài toán.
b) Tre giữ làng, giữ nước, giữ mái nhà tranh, giữ đồng lúa chín.
Câu 3 : (6 điểm) Thuyết minh về cây bút bi.
Đáp án đề thi giữa kì 1 văn 9 số 2
Câu 1:
– Chép đúng chính tả đoạn thơ cuối bài thơ Khi con tu hú (Tố Hữu)
Ta nghe hè dậy bên lòng
Mà chân muốn đạp tan phòng, hè ôi.
Ngột làm sao, chết uất thôi
Con chim tu hú ngoài trời kêu!
– Nội dung: Lòng yêu cuộc sống và niềm khát khao tự do cháy bỏng của người chiến sĩ cách mạng trong cảnh tù đày.
Câu 2: Giải thích lí do lựa chọn trật tự từ:
a) Từ in đậm “gặp”, “nhờ” thể hiện thứ tự trước sau của hoạt động đang diễn ra.
b) Từ in đậm “giữ làng”, “giữ nước”, “giữ mái nhà tranh”, “giữ đồng lúa chín” là đảm bảo sự hài hòa về mặt ngữ âm.
Câu 3: Thuyết minh về cây bút bi
* Mở bài: Giới thiệu về cây bút (một trong những đồ dùng học tập cần thiết của học sinh…)
* Thân bài:
– Lịch sử ra đời của bút bi:
- Ai là người chế tạo ra cây bút bi?
- Cây bút bi được sản xuất năm nào?
- Cụ thể: Do nhà báo Hung-ga-ri làm việc tại Anh tên là Laszlo Biro, sản xuất năm 1938…
– Hình dáng, cấu tạo: 2 phần
- Phần ruột: Gồm một ống mực nhỏ, một đầu được gắn với một viên bi có đường kính từ 0.7 đến 1mm gọi là ngòi bút, khi viết mực được in lên giấy là nhờ sự chuyển động của viên bi này (miêu tả, so sánh…)
- Phần vỏ: Hình tròn, bằng nhựa…
– Phân loại: Các loại bút bi trên thị trường: bút bấm, bút đậy nắp…
– Công dụng của bút bi: dùng để viết.
– Cách bảo quản và sử dụng.
* Kết bài: Đánh giá về đối tượng với khả năng, vai trò ứng dụng của nó trong thực tế.
Đề thi giữa kì 1 văn 9 số 3
I. ĐỌC – HIỂU (7,0 điểm)
Cho đoạn văn sau:
“Thiếp nếu đoan trang giữ tiết, trinh bạch gìn lòng, vào nước xin làm ngọc Mị Nương, xuống đất xin làm cỏ Ngu mĩ. Nhược bằng lòng chim dạ cá, lừa chồng dối con, dưới xin làm mồi cho cá tôm, trên xin làm cơm cho diều quạ, và xin chịu khắp mọi người phỉ nhổ”
Câu 1 : Đoạn văn trên trích trong tác phẩm nào? Của ai? Được viết bằng chữ gì? (1 điểm)
Câu 2 : Đoạn văn trên có dùng điển tích gì, nêu ý nghĩa của việc dùng các điển tích đó? (1 điểm)
Câu 3 : Nhân vật bày tỏ nỗi lòng trong đoạn văn trên là ai? Điều muốn bày tỏ là gì? (1 điểm)
Câu 4 : Bằng đoạn văn khoảng 10-12 câu, hãy phát biểu cảm nghĩ về nhân vật chính trong tác phẩm có đoạn trích trên. Gạch chân câu chủ đề của đoạn văn em trình bày. (4 điểm)
II. LÀM VĂN (3 điểm)
Trong một bài thơ có đoạn:
Ta nghe hè dậy bên lòng
Mà chân muốn đạp tan phòng hè ôi!
Ngột làm sao chết uất thôi
Khi con tu hú ngoài trời cứ kêu
Câu 1 : Đoạn thơ trên trích trong tác phẩm nào? Của ai? Viết trong hoàn cảnh nào? (1 điểm)
Câu 2 : Viết đoạn văn diễn dịch nêu cảm nhận của em về đoạn thơ trên? (Đoạn văn có sử dụng câu ghép chính phụ có quan hệ nguyên nhân – kết quả, xác định rõ câu ghép đó bằng cách gạch chân). (2 điểm)
Đáp án đề thi giữa kì 1 văn 9 số 3
I. ĐỌC – HIỂU (7,0 điểm)
Câu 1 :
– Đoạn văn trên trích trong văn bản: Chuyện người con gái Nam Xương (0,25đ)
– Thuộc tác phẩm: Truyền kì mạn lục (0,25đ)
– Tác giả: Nguyễn Dữ (0,25đ)
– Viết bằng chữ Hán (0,25đ)
Câu 2 :
– Dùng điển tích ngọc Mị Nương, cỏ Ngu mĩ (0,5đ)
– Ý nghĩa của việc dùng điển tích: Thể hiện sự trong sáng, thủy chung của Vũ Nương. (0,5đ)
Câu 3 :
– Nhân vật muốn bày tỏ nỗi niểm trong đoạn văn là Vũ Nương. (0,5đ)
– Muốn bày tỏ với trời đất để giải nỗi oan cho mình. (0,5đ)
Câu 4 :
– Viết đúng hình thức đoạn văn, số lượng không vượt quá hoặc ít quá 2 câu. (0,5đ)
– Nội dung (3,5đ)
- Ngay từ đầu đã được giới thiệu “Tính đã thùy mị nết na, lại thêm tư dung tốt đẹp”.
- Là vợ đảm đang, biết giữ gìn khuôn phép, một lòng một dạ chung thủy với chồng (thể hiện trong những cư xử khéo léo để gia đình không lâm vào cảnh thất hòa, dù người chống có tính đa nghi; trong lời dặn dò ân tình, đằm thắm khi tiễn chồng đi lính; chung thủy chờ chồng “cách biệt ba năm giữ gìn một tiết”).
- Là một người mẹ hiền, dâu thảo: vừa một mình nuôi dạy con thơ vừa làm tròn phận sự của một nàng dâu.
- Nạn nhân của chế độ nam quyền, của cuộc chiến tranh phong kiến phi nghĩa: cuộc hôn nhân của nàng không xuất phát từ tình yêu; phải đằng đẵng chờ chồng khi chồng đi chiến trận.
- Bị chồng nghi ngờ lòng chung thủy chỉ vì lời nói ngây thơ của con trẻ (chú ý các lời thoại của Vũ Nương: cố phân trần với chồng, biện bạch cho mình mà không được, đau khổ tuyệt vọng khi bị chồng mắng nhiếc, đánh đuổi đi, bị dồn vào bước đường cùng: phải tự vẫn ở bến Hoàng Giang để bảo toàn danh dự).
- Đoạn kết của truyện tuy mang màu sắc cổ tích (kết thúc có hậu) nhưng vẫn không làm mờ đi bi kịch của Vũ Nương: nàng không thể trở về dương thế sống bên cạnh chồng con được nữa.
II. LÀM VĂN (3 điểm)
Câu 1 :
– Tác phẩm: Khi con Tu hú (0,25đ)
– Của tác giả Tố Hữu (0,25đ)
– Hoàn cảnh ra đời: Viết khi tác giả đang bị nhốt trong nhà lao phủ Thừa Thiên. (0,5đ)
Câu 2 :
– Viết đúng hình thức đoạn văn(0,5đ)
– Nội dung cảm nhận được tâm trạng bức bối của người chiến sĩ trong tù ngục và dùng 1 câu ghép chính phụ có quan hệ nguyên nhân – kết quả, có xác định bằng cách gạch chân (2đ)
Đề thi giữa kì 1 văn 9 số 4
I. ĐỌC – HIỂU (4,0 điểm)
Dưới đây là một phần trong lệnh truyền của vua Quang Trung với quân lính:
“Quân Thanh sang xâm lấn nước ta, hiện ở Thăng Long, các ngươi đã biết chưa? Trong khoảng vũ trụ, đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị.(…) Các ngươi đều là những kẻ có lương tri, lương năng, hãy nên cùng ta đồng tâm hiệp lực, để dựng nên công lớn.”
(Trích Ngữ văn 9, tập một – NXB Giáo dục, 2012)
Câu 1 : Đoạn văn trên trích trong tác phẩm nào? Tác giả là ai?
Câu 2 : Nhà vua nói “đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị” nhằm khẳng định điều gì? Hãy chép 2 câu trong bài thơ “Sông núi nước Nam” có nội dung tương tự.
Câu 3 : Từ đoạn trích trên, với những hiểu biết xã hội, em hãy trình bày suy nghĩ (khoảng nửa trang giấy thi) về hình ảnh những người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng của dân tộc.
II. LÀM VĂN (6 điểm)
Cho câu thơ sau:
“Kiều càng sắc sảo mặn mà”
Câu 1 : Hãy chép chính xác những câu thơ tiếp theo miêu tả sắc đẹp của Thúy Kiều.
Câu 2 : Em hiểu như thế nào về những hình tượng nghệ thuật ước lệ “thu thủy”, “xuân sơn” ? Cách nói “Làn thu thủy nét xuân sơn” dùng nghệ thuật ẩn dụ hay hoán dụ? Giải thích rõ vì sao em chọn nghệ thuật ấy?
Câu 3 : Từ câu chủ đề sau: “Khác với Thúy Vân, Thúy Kiều có vẻ đẹp mặn mà cả tài lẫn sắc”.
Hãy viết nối tiếp khoảng 10 câu văn để hoàn thành một đoạn văn theo cách diễn dịch hoặc tổng – phân – hợp. Chỉ ra và phân tích cấu tạo một câu ghép đã sử dụng trong đoạn văn.
Đáp án đề thi giữa kì 1 văn 9 số 4
I. ĐỌC – HIỂU (4,0 điểm)
Câu 1 : (1 điểm)
– Đoạn văn trên trích trong tác phẩm “Hoàng Lê Nhất Thống Chí”. (0,5đ)
– Tác giả là nhóm Ngô Gia Văn Phái, gồm có Ngô Thì Chí (1758-1788) và Ngô Thì Du (1772-1840). (0,5đ)
Câu 2 : (1 điểm)
– Lời nói của nhà vua “đất nào sao ấy, đều đã phân biệt rõ ràng, phương Nam, phương Bắc chia nhau mà cai trị” nhằm khẳng định chủ quyền của đất nước và kín đáo bày tỏ niềm tự hào về chủ quyền đất nước và sự bình đẳng giữa phương Bắc với phương Nam. (0,5đ)
– Trong bài thơ Sông núi nước Nam của Lý Thường Kiệt có hai câu mang nội dung tương tự:
Sông núi nước Nam, vua Nam ở
Vằng vặc sách trời chia xứ sở
(Nam quốc sơn hà Nam đế cư
Tiệt nhiên định phận tại thiên thư) (0,5đ)
Câu 3 : Viết đoạn văn (2 điểm)
*Về hình thức (0,5 điểm):
- Đoạn văn có liên kết, mạch lạc.
- Có độ dài khoảng nửa trang giấy thi
*Về nội dung (1,5 điểm):
Học sinh có thể triển khai bài viết theo nhiều cách khác nhau. Và đây là một số gợi ý để tham khảo :
- Việt Nam là một quốc gia nằm ven biển. Lãnh thổ bao gồm đất liền và rất nhiều hải đảo. Bên cạnh những người chiến sĩ bảo vệ chủ quyền của đất nước trên đất liền, trên không, chúng ta không thể không nghĩ tới những người chiến sĩ ngày đêm bảo vệ biển đảo thiêng liêng của dân tộc.
- Các anh là những người sống trong một khung cảnh có nhiều khó khăn gian khổ: sống giữa biển khơi, đầy nắng gió, thường xuyên gặp phải bão tố.
- Cuộc sống của các anh thiếu thốn phương tiện so với người dân ở đất liền: thiếu nước ngọt, thiếu sách báo,…
- Xa gia đình, xa người thân nên nhiều khi phải trải qua những nỗi buồn da diết vì nhớ nhà,… – Tuy đầy gian khổ và khó khăn nhưng những điều này không làm mềm đi ý chí quyết tâm bảo vệ chủ quyền tổ quốc, bảo vệ cuộc sống bình yên của người dân, nhất là những ngư dân trên biển cả.
- Đất nước được toàn vẹn, cuộc sống vẫn phát triển bình thường, hàng ngày các em được bình yên đến trường, bữa cơm mỗi ngày không thiếu những sản phẩm của biển cả,… nhờ có một phần không nhỏ công sức và sự hy sinh thầm lặng của các anh.
- Hình ảnh của các anh chiến sĩ ngoài biển đảo là những hình ảnh hào hùng ẩn chứa vẻ đẹp của sự hy sinh vì nghĩa lớn.
II. LÀM VĂN (6 điểm)
Câu 1 : Chép chính xác: (0.5điểm)
Kiều càng sắc sảo mặn mà
So bề tài sắc lại là phần hơn
Làn thu thủy nét xuân sơn
Hoa ghen thua thắm liễu hờn kém xanh
Câu 2 : (2 điểm)
+ Giải thích
– Thu thủy : là nước mùa thu (0,25đ)
– Xuân sơn : là núi mùa xuân (0,25đ)
– Làn thu thủy nét xuân sơn : mắt đẹp, trong sang như nước mùa thu, long mày đẹp, thanh thoát như nét núi mùa xuân. (0,5đ)
+ Cách nói “Làn thu thủy nét xuân sơn” dùng nghệ thuật ẩn dụ.(0,5đ)
– “Làn thu thủy nét xuân sơn” dùng nghệ thuật ẩn dụ. Vì thông qua vẻ đẹp trong sáng của làn nước mùa thu, nét thanh thoát của núi mùa xuân để làm nổi bật vẻ đẹp của đôi mắt Thúy Kiều – chiều sâu của tâm hồn. (0,5đ)
Câu 3 : Viết đoạn văn (3,5 điểm)
*Về hình thức (1 điểm):
- Trình bày đúng đoạn văn diễn dịch hoặc tổng – phân – hợp, có liên kết mạch lạc: 0,25 điểm
- Có đủ số câu theo yêu cầu, có đánh số thứ tự từ câu đầu đến câu cuối: 0,25 điểm.
- Trong đoạn văn có sử dụng câu ghép: phân tích đúng ngữ pháp, hợp nội dung, có chú thích ở dưới mới được (0,5 điểm).
*Về nội dung (2,5 điểm): Phân tích vẻ đẹp – tài sắc của Thúy Kiều.
Đoạn văn cần đảm bảo những nội dung sau:
+Vẻ đẹp:
- Vẻ đẹp lộng lẫy kiêu sa của bậc tuyệt thế giai nhân
- Tính cách sắc sảo mặn mà
- Dự báo số phận long đong, đau khổ của Thúy Kiều
+Tài năng:
- Thông minh vốn sẵn tính trời
- Thơ, ca, nhạc, họa đều giỏi
- Sáng tác bản nhạc “Bạc mệnh” => người con gái thông minh, có cuộc sống nội tâm phong phú, nhưng cũng là một người đa sầu đa cảm.
⇒ Chân dung Thúy Kiều là chân dung mang tính cách, số phận. Vẻ đẹp của Kiều làm cho tạo hóa phải ghen ghét, dẫn đến nhiều người phải đố kị về vẻ đẹp đó, nên số phận của nàng mới gặp nhiều trái ngang đau khổ. Thúy Kiều là nhân vật khắc họa rõ nhất câu nói “Hồng nhan bạc mệnh”.
Tải bộ đề thi giữa kì 1 văn 9 có đáp án
Để tải bộ đề thi giữa kì 1 văn 9 năm 2022 – 2023 kèm đáp án chi tiết, bạn có thể truy cập tại đây:
[su_button url=”https://docs.google.com/document/d/1fi6W68cf9BWX_YT9aPU0T3gPJTIw0_BuX9B3G5g6CJ4/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 MÔN VĂN LỚP 9[/su_button]
Xem thêm:
- Bộ đề thi giữa kì 1 toán 9 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
- Tổng hợp các công thức lượng giác lớp 9, 10, 11 đầy đủ nhất
- Tổng hợp các tác phẩm văn học lớp 9 kì 1 và kì 2 và tác giả đầy đủ nhất
Trên đây là tổng hợp 4 bộ đề thi giữa kì 1 văn 9 giúp cho các bạn học sinh có thể thêm nguồn tham khảo để luyện tập trước. Hy vọng, từ các bộ đề này sẽ phần nào luyện tập cho các bạn làm quen với các dạng bài, để có một tâm thế vững vàng và tự tin cho kì thi sắp tới. Chúc các bạn học sinh có một kì thi thật tốt!
Tổng hợp 7 đề thi tiếng Anh lớp 7 giữa học kì 1 chương trình mới có đáp án
Dưới đây là tổng hợp 7 đề thi tiếng Anh lớp 7 – Trung học cơ sở giữa học kì 1 chương trình mới có đáp án chi tiết được tải nhiều nhất hiện nay. Mời các bạn cùng tham khảo để nắm được kiến thức và nội dung trọng tâm, từ đó chuẩn bị cho kỳ thi sắp tới.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 1
Choose the word that has the underlined part pronounced differently from the others.
1. A. go B. photo C. piano D. collect
2. A. watch B. catch C. school D. teach
Choose the word which is stressed differently from the others.
3. A. temperature B. stomachache C. adult D. advice
4. A. recycle B. benefit C. provide D. encourage
Choose the best answer among A, B, C or D that best completes each sentence.
5. ________are those who do not have a home and really need help.
A. elderly people
B. sick children
C. homeless people
D. disabled people
6. She often _______money to charitable organisations.
A. donate
B. volunteer
C. recycle
D. plant
7. I think I_______him before.
A. meet
B. met
C. will meet
D. have met
8. When I was a little girl, I often_________ the piano.
A. play
B. played
C. plays
D. have play
9. Eat______junk food. It makes you fat!
A. less
B. fewer
C. more
D. many
10. I have temperature, ____I feel tired.
A. and
B. or
C. but
D. so
11. She looks very red. She was outdoors all day yesterday. I think she has __________.
A. sunburn
B. headache
C. toothache
D. flu
12. My grandparents _____exercise in their free time.
A. play
B. collect
C. go
D. do
13. If you always buy flowers and put them in a vase to display in your house, your hobby is ________.
A. collecting flowers
B. arranging flowers
C. planting trees
D.bird-watching
14. They hate ________noodles. They prefer rice.
A. eating
B. eat
C. eats
D. ate
15. I find this hobby________ because carved eggshells are unique gifts for families and friends.
A. interest
B. interested
C. to interest
D.interesting
16. Go Greens _________the environment.
A. gives
B. protects
C. donates
D. recycles
Match the clauses in A with the clauses in B to form meaningful sentences.
|
A |
B |
| 17. I want to eat some junk food, | a. and I feel tired. |
| 18. I don’t want to be tired tomorrow, | b. or I can cycle to school. |
| 19. I have a temperature, | c. but I am putting on weight. |
| 20. I can exercise every morning. | d. so I should go to bed early. |
Read the text and mark the sentences as True (T) or False (F).
Dentists say that the most important part of tooth care happens at home. So, what should we do to have good oral teeth?
First of all, we should brush our teeth at least twice a day – after breakfast and dinner. To keep our teeth healthy, we should brush thoroughly for two minutes. Move the brush back and forth and make sure to clean the back, front and top sides of each tooth. Second, among a lot of toothbrushes in the supermarket, we should choose a small-headed soft toothbrush. It can reach all areas of the mouth and doesn’t harm our teeth and gums. We should also replace the toothbrush every three months.
Third, we should use mouthwash after brushing. Each tooth has five sides, but a toothbrush cleans only three of them. The mouthwash helps us clean teeth completely. Remember to spit it out.
Fourth, we should choose the best food for the health of our teeth which includes cheeses, chicken or other meat and nuts. These food provide the calcium which helps strengthen the teeth. Some vegetables like garlic, ginger or pepper can be used as home remedies for a toothache. Try to advoid snacks, sugary food or soda.
Last but not least, we should visit our dentist at least every six months and every time that we have a problem with our teeth.
|
Mark the sentences |
T/F |
| 21. Tooth care doesn’t include taking care of the teeth at home. | |
| 22. We should brush our teeth for one minute. | |
| 23. Among a lot of kinds of mouthwash, we should choose carefully. | |
| 24. Snacks and sugary food are harmful for the teeth. | |
| 25. We should choose a toothbrush with a small head. |
Read the text. Choose the best answer A, B, C or D.
WHAT IS COMMUNITY SERVICE?
Community service is (26)_________to help those in your community. It might be something that is done once or on a regular basis. Community (27)__________ is often referred to as “giving back to your (28)________”. It can be done by an (29)__________ or an organisation. Community service is giving your time without being (30)__________, whether it is to help the less fortunate or to help clean up your community.
26. A. volunteer B. volunteering C. voluntary D. to volunteer
27. A. benefit B. product C. service D. gift
28. A. community B. volunteer C. friend D. help
29. A. adult B. individual C. elderly person D. area
30. A. given B. donated C. paid D. provided
WRITING.
I. Complete the following sentences using the cues given.
1. We/ buy/ new car/ last weekend.
……………………………………………………………………………………………………………………………………..
2. She/ not write/ her grandparents/ yet.
……………………………………………………………………………………………………………………………………..
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 1
| 1D | 2C | 3D | 4B | 5C | 6A | 7D | 8B | 9C | 10D |
| 11A | 12D | 13B | 14A | 15D | 16B | 17C | 18D | 19A | 20B |
| 21F | 22F | 23F | 24T | 25T | 26B | 27C | 28A | 29B | 30C |
WRITING
1. We bought a new car last weekend.
2. She hasn’t written to her grandparents yet.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 2
Circle the word that has the underlined part pronounced differently from the others.
| 1. A. answer | B. teacher | C. butter | D. birth |
| 2. A. surprise | B. alone | C. neighbour | D. burn |
| 3. A. of | B. fat | C. few | D. safe |
| 4. A. spring | B. visit | C. present | D. usually |
| 5. A. curl | B. keen | C. glove | D. cook |
Choose the best answer to complete the sentences.
1. -“What would you like to drink now?” – “_______________.”
A. No, thanks B. Yes, please C. I like to do nothing D. Orange juice, please
2. All of us enjoy _______ to classical music.
A. listen
B. listens
C. listening
D. listened
3. She worked very hard, _______she passed all her exams.
A. because
B. and
C. so
D. but
4. Hoa looks red. She was outdoors yesterday. Perhaps she has _______
A. flu
B. sunburn
C. spots
D. stomachache
5. My family has decided to use _________ electricity by using more solar energy instead.
A. more
B. less
C. much
D. fewer
6. I …………… playing board games interesting because I can play them with my friends.
A. find
B. think
C. say
D. tell
7. -” Would you like me to turn off your computer?
– ” ______________. I’ll do it myself”
A. No, thanks
B. Yes, please
C. Don’t do it
D. Of course
8. You like playing monopoly or chess, your hobby may be _______.
A. collecting things
B. playing sports
C. dancing
D. board games
Read and fill in the blanks with ONE word given in the box. There is one Extra word you don’t need to use. (1.0 pt)
| hobby improve when writes because difficult |
My Favorite Hobby
My name is Sara. My favorite _____________(1) is reading. I enjoy reading a book when I am free. I started to do it ______________(2) I was four years old. The first time I did it, I felt interested. So I kept reading. The teachers always taught me to read the difficult words. I was happy when I read a story with a happy ending. I was thrilled when I read a detective story.
I enjoy reading ______________(3) I like to explore the imaginative world of my favorite author, J.K. Rowling who _____________(4) ” Harry Potter” . There are a lot of advantages of reading. Reading can make me relaxed and calm. I can also learn new vocabulary items. Then I can further _________________(5) my English. Moreover, it can give me an unlimited imagination, so I can write books in the future. I can learn the different cultures and customs of other countries in the world too.
I read at least one hour every day. I read books by myself. I usually read it at home. I wish I could read different kinds of books because it might be very challenging.
Read the following passages and answer the questions below.
Oil painting
Since the 18th century, under the impact of society, culture, and technology, oil painting has undergone dramatic changes. They are rebellious but passionate, and prosperous.
Watercolor paintings
Watercolor paintings are considered a unique way to creatively represent dreams, illusions, emotions, and bright feelings using water-soluble pigments.
Sketch (Tranh phác họa)
Van Gogh did not begin painting until his late twenties. He produced more than 2,000 artworks, consisting of around 900 paintings and 1,100 sketches.
Portrait (Tranh chân dung)
The Mona Lisa is a famous 16th-century portrait by Leonardo da Vinci. The true identity of the woman pictured in the portrait remains unknown, despite intensive researches by art historians.
1. What kind of painting is rebellious?
=> ……………………………………………………………………………..
2. Who was famous for Sketch?
=> ……………………………………………………………………………..
3. When did Leonardo da Vinci draw the portrait ‘ The Mona Lisa”?
=> ……………………………………………………………………………..
Combine each pair of the following sentences into one, using the suggested conjunctions in the brackets.
1. Mr. Hai usually has stomach problems. He eats dinner very close to the bedtime. (so)
=> …………………………………………………………………………………..
2. My dad has a lot of carved eggs. He has never sold any of them. (but)
=> ………………………………………………………………………
3. You will get a breathing problem. Clean your bed room more regularly. (or)
=> ……………………………………………………………………….
II. Rearrange the jumbled words to make meaningful sentences. (1.0 pt)
1. It/ be/ good idea/ eat/ different/ kind/ fruit/ vegetable/ every day.
=> ………………………………………………………………………
2. My brother/ not like/ ice-skating/ because/ think/ it/ dangerous.
=> …………………………………………………………………………
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 2
Circle the word that has the underlined part pronounced differently from the others.) (5 items x 0,1 = 0,5 pt)
1. D
2. D
3. A
4. B
5. C
Choose the best answer to complete the sentences. (8 items x 0,25 =2,0 pts)
1. D
2. C
3. C
4. B
5. B
6. A
7. A
8. D
Read and fill in the blanks with ONE word given in the box. There is one Extra word you don’t need to use. (5 items x 0,2 = 1,0 pt)
1. hobby 2. when 3. because 4. writes 5. improve
Read the following passages and answer the questions below.
1. It is Oil painting.
2. Van Gogh was famous for it.
3. He painted it in the sixteenth century.
Combine each pair of the following sentences into one, using the conjunctions in brackets
1. Mr. Hai eats dinner very close to the bedtime, so he usually has stomach problems.
2. My dad has a lot of carved eggs, but he has never sold any of them.
3. Clean your bed room more regularly or you will get a breathing problem.
Rearrange the jumbled words to make meaningful sentences.
1. It’s a good idea to eat different kinds of fruit and vegetables every day.
2. My brother doesn’t like ice-skating because he thinks it is dangerous.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 3
I. Choose the word in each group that has the underlined part pronounced differently from the rest. (1 mark):
| 1. A. chair | B. school | C. couch | D. children |
| 2. A. sometimes | B. moment | C. stove | D. close |
| 3. A. biology | B. geography | C. physics | D. fly |
| 4. A. homework | B. house | C. hour | D. here |
II. Choose the best words by circling the letter A,B,C or D. (2 marks)
1. How …….. is it from your house to school?
A. far
B. long
C. old
D. tall
2. What ……… intelligent boy!
A. the
B. a
C. an
D. is
3. Would you like some coffee?- __________
A. Yes, please
B. Of course
C. No, thanks
D. Both A and C are correct.
4. This car is the ……. expensive of the four car.
A. Best
B. more
C. good
D. most
5. They enjoy …….. TV.
A. to watch
B. watching
C. to watching
D. watched
6. A ………….. work on a farm.
A. doctor
B. farmer
C. teacher
D. journalist
7. She is very happy …….. you again.
A. meet
B. meets
C. to meet
D. meeting
8. He is in class 7A and …………………………. am I.
A. too
B. so
C. but
D. by
III. Give the correct form of the verbs in the bracket. (2 marks)
1. Trang (not have) any friends in Ha noi.
2. Some boys and girls (play) marbles at the moment.
3. The students (visit) their old teacher next week?
4. Mr Nam usually (watch) TV in his free time?
IV. Fill in the blanks with the correct form of the words in the capital letters (1 mark):
1. Today Lien is not………………..because she misses her parents HAPPINESS
2. Living in the city is………………than living in the countryside NOISY
3. In electronics, we learn to repair. …………………….appliances. HOUSE
4. My. ………………….is tall and beautiful. TEACH
V. Read the passage carefully then answer the questions: (2 marks)
Linda lives with her parents in a big house in HCM City. She is from England. She is thirteen. She has blue eyes and black hair. She is studying at International Language School. She can speak French, English and Vietnamese. But she doesn’t speak Vietnamese fluently. She often goes to French speaking club on Sunday mornings. She likes Vietnamese people very much because they are friendly.
1. Where is Linda from?
……………………………………………………………………………..
2. How many languages can she speak?
………………………………………………………………
3. Does she speak Vietnamese fluently?
……………………………………………………………..
4. Why does she like Vietnamese people?
…………………………………………………………
VI. Read the following passage and choose the best option for each numbered blank.
Do you want to be fitter and healthier? Would you like to look younger? Do you want to feel (1) ___________ relaxed? Then try a few days at a health farm. Health farms are becoming (2) ___________ of the most popular places (3) ___________a short break. I went to Henley Manor for a weekend. It’s (4) ___________ largest health farm in the country but it isn’t the most expensive. After two days of exercise and massage I (5) ___________ten times better. But the best thing for me was the food. It was all very healthy of (6) ___________ , but it was expensive too!
If you’re looking for something a (7) ___________cheaper, try a winter break. Winter is the darkest and the coldest (8) ___________of the year, and it can also be the (9) ___________ time for your body. We all eat too (10) ___________and we don’t take enough exercise. A lot of health farms offer lower prices from Monday to Friday from November to March.
|
1. A. like |
B. more | C. less | D. similar |
| 2. A. once | B. first | C. one | D. none |
| 3. A. with | B. of | C. to | D. for |
| 4. A. the | B. an | C. a | D. x |
| 5. A. feel | B. felt | C. fell | D. fall |
| 6. A. all | B. out | C. course | D. them |
| 7. A. little | B. few | C. a little | D. a few |
| 8. A. period | B. moment | C. time | D. part |
| 9. A. worst | B. good | C. best | D. great |
| 10. A. many | B. a lot | C. lot of |
D. much |
VII. Arrange the following words to make correct sentences. (1 mark).
1. play/ will/ soccer/ this/ afternoon/ they.
…………………………………………………………………………………
2. my/ is/ favorite/ English/ subject.
…………………………………………………………………………………
VIII. Complete the following sentences with the suggested words. (1 mark).
1. It / difficult/ find/ apartment / Ho Chi Minh City?
……………………………………………………………………………………..
2. They/ listen/ music/ now.
……………………………………………………………………………………..
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 3
I. Choose the word in each group that has the underlined part pronounced differently from the rest.
1. B
2. A
3. D
4. C
II. Choose the best words by circling the letter A, B, C or D.
1. A
2. C
3. D
4. D
5. B
6. B
7. C
8. B
III. Give the correct form of the verbs in the bracket.
1. doesn’t have 2. are playing 3. will visit 4. watches
IV. Fill in the blanks with the correct form of the words in the capital letters:
1. happy
2. noisier
3. household
4. teacher
V. Read the passage carefully then answer the questions
1. She is from England.
2. She can speak three languages.
3. No, she doesn’t.
4. She likes Vietnamese people very much because they are friendly.
VI. Read the following passage and choose the best option for each numbered blank.
|
1. B |
2. C | 3. D | 4. A | 5. B |
| 6. C | 7. A | 8. C | 9. A |
10. D |
VII. Arrange the following words to make correct sentences.
1. They will play soccer this afternoon.
2. My favorite subject is English/English is my favorite subject.
VIII. Complete the following sentences with the suggested words. (1 mark):
1. Is it difficult to find an apartment in Ho Chi Minh City?
2. They are listening to music now.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 4
A. GRAMMAR, VOCABULARY AND PHONETICS
Question 1.
*Choose the best answer for each of the following sentences
1. Will you ………….making models in the future?
A. pick up
B. look for
C. take up
D. find
2. His parents are always proud …………. him ?
A. about
B. of
C. on
D. with
3. Have you ever……………to Sa Pa?
A. goes
B. be
C. go
D. been
4. I ……playing board games interesting because I can play them with my friends.
A. think
B. find
C. say
D. tell
5. I like watching TV ……….. it’s entertaining and educational.
A. so
B. but
C. although
D. because
6. It’s good to____ blood because you can save people’s lives.
A. helping
B. used
C.collecting
D. donate
* Choose the word that has the underlined part pronounced differently from the others.
7. A. goal B gold C. original D.girl.
8. A. studied B. washed C. looked D.watched
* Choose the word with the different stress syllable.
9. A. statistics B. history C. concentrate D. different
10.A. wonderful B. beautiful C. prediction D. television
Question 2. Give the right form of the verbs in brackets.
1. I (hear) ………………the good news from Mary a few minutes ago.
2. …………………..you ever (visit)…………………Da Nang ?
3. Don’t worry we (go) …………………..swimming with you tomorrow.
4. It’s boring ( watch )…………………………. television everyday.
5. You (see) ……………….the film on television last night?
6. George is interested in (take)………………. an art class
B. Reading
Question 1. Read the article about Angel Falls. Then answer the questions.
Dear Mira,
Thanks for your letter. Now I’ll tell you about my hobbies.
My favourite hobby is knitting. It is strange, isn’t it?. My mother taught me to knit two years ago. Now I can knit scarves and sweaters. It’s great when I can give them to my relatives and friends as gifts. Knitting is also imaginative because you can knit anything you can imagine of. Besides, it is quite cheap. You only need a pair of needles and some wool.
I’m sending you a scarf next month. I’m knitting it. I hope you’ll like it.
Best wishes,
Vy
1. What is Vy’s hobby?
…………………………………………………………………….
2. Did she learn this hobby from her father?.
………………………………………………………………………………
3. How does she feel when she can give the scarves and sweaters to her relatives and friends ?.
…………………………………………………………………………………
Question 2. Read the text and choose the best answer A, B, C or D to fill each blank .
My friends and I have written a (1) . We have decided to (2) it for our school. I have already built the set. Karen has just finished the (3) for us to wear. I haven’t learned the (4) yet, so I am a bit nervous, but I’m excited too. I haven’t been in a play before. I can’t wait!
1.A. film B. song C. play D. club
2.A. perform B. make C. take D. build
3.A. stage B. actors C. play D. costumes
4.A. script B. scripts C. play D. lessons
C. Writing
Question 1. Rearrange the words below to make meaningful sentenses.
1.We / collected / books / clothes / street children/ have/and/ for /used .
………………………………………………………………………………………………………………………………..
2. doing / finds / interesting/ he/ service / community .
………………………………………………………………………………………………………………………………..
3.not/ pass / did / Minh / lazy/ was / so/ he/exam/ the.
………………………………………………………………………………………………………………………………..
4. important / study / to / It / is / English .
………………………………………………………………………………………………………………………………..
Question 2. Rewrite the following sentences, beginning as shown, so that the meaning stays the same.
1/ Hoa was sick, so she could not go to school yesterday.
→ Because ……………………………………………………………………………….
2. The last time I saw him was 3 years ago
→ I haven’t ……………………………………………………………………………
3. I find making pottery interesting.
→ I think………………………………………………………………………………………………………..
4. My sister is interested in reading comics.
→ My sister enjoys………………………………………………………………………………………..
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 4
A. GRAMMAR,VOCABULARY AND PHONETICS
Question 1.
|
1. C |
2. B | 3. D | 4. B | 5. D |
| 6. D | 7. C | 8. A | 9. A |
10. C |
Question 2. Give the right form of the verbs in brackets:
|
1 . heard |
2. Have…visited | 3. will go |
| 1. to watch | 2. Did …….see |
3. taking |
B. Reading
Question 1. Read the text and answer the questions:
1. Her favourite hobby is knitting
2. No,she doesn’t.
3. She feels great when she can give them to her relatives and friends as gifts.
Question 2. Read the text and choose the best answer A, B, C or D to fill each blank:
|
1.C |
2.A | 3.D |
4.B |
C. Writing
Question 1. Rearrange the words below to make meaningful sentenses. Bottom of Form
1. We have collected used books and clothes for street children .
2. He finds doing community service interesting .
3. Minh was lazy so he did not pass the exam .
4. It’s important to study English .
Question 2. Rewrite the following sentences, beginning as shown, so that the meaning stays the same. Bottom of Form
1. Because Hoa was sick,she could not go to school yesterday.
2. I haven’t seen him for 3 years.
3. I think making pottery is interesting .
4. My sister enjoys reading comics.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 5
I. Choose the word whose underlined is pronounced differently (1 mark)
1. A. calorie B. musical C. cinema D. community
2. A. again B. allergy C. organization D. gardening
3. A. school B. chemistry C. christmas D. champion
4. A.laugh B. rough C. enough D. neighbor
II. Choose the correct word or phrase to fill in each of the following sentences (3 marks)
1. Her parents still live there ………. her grandparents.
A. for B. at C. with D. on
2. Lan is ………… than Hoa
A. tallest B. tall C. taller D. more tall
3. …………… do you live?
A. Who B. What C. Which D. Where
4. ……………… are you talking to?
A. Who B. What C. Which D. Where
5. What …………….. your telephone number?
A. is B. are C. does D. do
6. Nga lives …………. 52 Nguyen Hue Street.
A. on B. in C. at D. under
7. …………… does your father do?
A. When B. Where C. What D. Which
8. Tomorrow my family …………………. to Ho Chi Minh City.
A. is B. is going to go C.is going D. goes
9. My mother takes care …………… sick children.
A. about B. in C. at D. of
10. He works ……………. the farm.
A. on B. in C. about D.at
11. Are there ………. pens on the table? Yes, there are.
A. any B. some C. much D. a
12. …………………… a beautiful day!
A. It B. Which C. Where D. What
III. Complete the sentences with on, in, at, in front of (1 mark).
1. My birthday is………………..June eighth.
2. I live…………..Gio Quang.
3. I get up…………….6 o’clock every day.
4. My house is………………………..a lake.
IV. Supply the correct form of the verbs in brackets (2,5 marks).
My aunt Thuy (live) ……………. (1) in Ha Dong. She (work) …………………(2) in a hospital in the centre of Ha Noi. Every morning, she (catch) ………………(3) a bus to her hospital. Her work is (take) ……………..(4) care of sick children. She (love) ……………..(5) the children. She always (say) …………(6) that children (be) …………(7) very lovely. Now she (do) ……………………(8) her job with great pleasure. But next year she (go)………….(9) to Ho Chi Minh City with her husband . She (be)………………(10) very unhappy.
V. Answer the questions (2,5 marks).
1. What ‘s your family name?
……………………………………………………………………………
2. How do you get to school?
……………………………………………………………………………
3. How far is it from your house to school?
……………………………………………………………………………
4. What will you be on your next birthday?
…………………………………………………………………………….
5. Where are you going to go next Sunday?
…………………………………………………………………………….
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 5
I. Choose the word whose underlined is pronounced differently
1. C
2. B
3. D
4. D
II. Choose the correct word or phrase to fill in each of the following sentences
1. C
2. C
3. D
4. A
5. A
6. C
7. C
8. B
9. D
10. A
11. A
12. D
III. Complete the sentences with on, in, at, in front of
1. On
2. In
3. At
4. In front of
IV. Supply the correct form of the verbs in brackets
1. Lives
2. Works
3. Catches
4. Taking
5. Loves
6. Says
7. Is
8. Is doing
9. Will go
10. Is
V. Answer the questions
1. My family name is…………….
2. I go to school by bike.
3. It is about 2 kilometers.
4. I will be 14 on my next birthday.
5. I am going to go to the zoo next Sunday.
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 6
Exercise 1: Choose the word whose underlined part is pronounced differently from the others
|
1. A. danced |
B. helped | C. watched | D. enjoyed |
|
2. A. calorie |
B. labour | C. community |
D. volunteer |
| 3. A. game | B. gym | C. girl |
D. bag |
Exercise 2: Choose the correct answer
1. I enjoy reading ______________ it develops my imagination.
A. and
B. but
C. so
D. because
2. To help people with transportation, we can __________ rides to the elderly.
A. ask
B. give
C. donate
D. help
3. My favourite hobby is _______. I spend most of my free time making vases and bowls from clay.
A. woodcarving
B. pottery making
C. model making
D. birdwatching
4. _______ do you do volunteer work? – Every weekend.
A. How long
B. How far
C. How much
D. How often
5. Have you ever taken part _______ volunteer work?
A. for
B. to
C. in
D. with
6. She’s got a high _______ – almost 40°.
A. flu
B. headache
C. sore throat
D. temperature
7. Mary is _______ weight because she eats too much junk food.
A. getting over
B. putting on
C. taking up
D. throwing away
8. Stay outdoors ________ and do _________ physical exercises.
A. more – less
B. less – less
C. more – more
D. less – more
9. Don’t read or study when there is not enough light because it is ________ to your eyes.
A. harm
B. harmful
C. harmless
D. unharmed
10. My aunt often ___________ money to charitable organizations to help street children and the homeless.
A. makes
B. does
C. donates
D. send
Exercise 3: Supply the correct form of the words in brackets
1. Mike’s hobby is listening to music. He gets a lot ___________ from listening to music. (enjoy)
2. One third of children in the U. S. is ___________ or obese. (weigh)
3. Junk food is ___________, so we shouldn’t eat too much junk food. (health)
Exercise 4: Write the correct tense or form of the verbs in brackets
1. We ________________ (not do) any volunteer work five years ago.
2. I think people ________________ (eat) more healthy food in the future.
3. ______________ (Alex/ ever/ be) to Seattle? ~ Yes, he ______________ (be) to Seattle once.
4. Be a Buddy ________________ (establish) in 2011.
5. My mother enjoys ________________(do) charitable work.
Exercise 5: Read the passage and answer the questions
We send young people of different nationalities on expeditions around the world. Our volunteers get the chance to work with local people to learn about different cultures.
There are ten expeditions every year. Each expedition lasts for ten weeks and takes 150 volunteers. They go to countries such as Chile, Namibia, Mongolia and Viet Nam. Some of our volunteers work with local people to provide facilities, for example, building schools. Others work in national parks or help scientists to do environmental research.
These adventurous, young people come from all over the world. To become a volunteer, you have to be between 17 and 25; you have to speak some English and you also have to be enthusiastic, flexible and hard-working members of a team.
1. Who goes on the expeditions?
____________________________________________
2. How many expeditions are there every year?
____________________________________________
3. How long does each expedition last?
____________________________________________
4. What do the volunteers help scientists?
____________________________________________
5. Which language must we know to become a volunteer?
____________________________________________
Exercise 6: Rewrite the following sentences without changing its meaning
1. I spend twenty minutes walking to school every morning.
It takes ______________________________________
2. I find losing weight very difficult.
It’s _________________________________________
3. He hasn’t smoked cigarettes for a month.
The last time _________________________________
Exercise 7: Arrange these words to make meaningful sentences.
1. you/ Have/ finished/ homework/ your/ yet/?
_____________________________________________
2. printer/ under/ This/ guarantee/ is/.
_____________________________________________
3. vacation/ since/ We/ haven’t/ last/ had/ a/ year/.
_____________________________________________
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 6
Exercise 1: Choose the word whose underlined part is pronounced differently from the others
1. D
2. D
3. B
Exercise 2: Choose the correct answer
|
1. D |
2. B | 3. B | 4. D | 5. C |
| 6. D | 7. B | 8. C | 9. B |
10. C |
Exercise 3: Supply the correct form of the words in brackets
1. Mike’s hobby is listening to music. He gets a lot enjoyment from listening to music.
2. One third of children in the U. S. is overweight or obese.
3. Junk food is unhealthy, so we shouldn’t eat too much junk food.
Exercise 4: Write the correct tense or form of the verbs in brackets
1. We didn’t do any volunteer work five years ago.
2. I think people will eat more healthy food in the future.
3. Has Alex ever been to Seattle? ~ Yes, he has been to Seattle once.
4. Be a Buddy was established in 2011.
5. My mother enjoys doing charitable work.
Exercise 5: Read the passage and answer the questions
1. Young people of different nationalities go on the expeditions.
2. There are ten expeditions every year.
3. It lasts for ten weeks.
4. They help scientists to do environmental research.
5. We have to speak English to become a volunteer.
Exercise 6: Rewrite the following sentences without changing its meaning
1. It takes me twenty minutes to walk to school every morning.
2. It’s very difficult for me to lose weight.
3. The last time he smoked was a month ago.
Exercise 7: Arrange these words to make meaningful sentences.
1. Have you finished your homework yet?
2. This printer is under guarantee
3. We haven’t had a vacation since last year
Đề thi tiếng Anh lớp 7 giữa học kì 1 số 7
Choose the word with a different way of pronunciation in the underlined part.
| 1. A. developed | B. visited | C. planted | D. needed |
| 2. A. bird | B. girl | C. sister | D. first |
| 3. A. hobby | B. hour | C. hotel | D. hot |
Fill each blank with the present simple, present continuous or past simple form of the verb in brackets
1. When Tom was a teenager, his hobby ___________ (be) horse riding.
2. Do you know that the sun always ___________ (rise) in the East?
3. Look! Toby ___________ (have) some fast food again!
4. Trung never ___________ (watch) TV before finishing all his homework.
Choose the best option to complete each sentence
1. Tom is having a lot of fast food! He needs to change his ___________.
A. hobby
B. diet
C. condition
2. You can use this ___________ to stick these pieces of color paper to decorate your dollhouse.
A. nail
B. glue
C. model
3. Some hobbies can help students learn to be ___________ with their work.
A. patient
B. popular
C. valuable
4. They have decided to clean up the neighbourhood __________ it is full of rubbish.
A. so
B. because
C. but
5. We came to the remote village and _________ meals for homeless children.
A. cooked
B. made
C. do
6. He ate a lot of fried food, so he __________ fat quickly.
A. get
B. got
C. will get
Read the passage. Circle the best answer A, B, or C to each of the questions.
Judo, one of the most popular martial arts, comes from Japan and it is quite well-known in Viet Nam. When we do judo, we will learn some basic techniques in throwing, grappling, and striking. We learn them carefully and steps by steps so that we do not have to worry too much about injuries. Judo teaches us how to train our bodies and minds as well as how to use our energy in the best way. It first appeared in the Olympic Games in Tokyo in 1964 and since 1972 it has been an official event in the Olympic Games. Vietnamese judokas – people who do judo – have won some international recognition and are trying their best to win first medals in the Olympic Games.
1. What is the passage mainly about?
A. The development of judo.
B. The development and benefits of judo.
C. The development of judo in Viet Nam.
2. What does the word It in line 6 mean?
A. Energy.
B. Mind.
C. Judo.
3. What is one of the benefits of practising judo?
A. Knowing how to throw people.
B. Learning to control our bodies.
C. Winning medals in competitions.
4. When did Judo first appear in the Olympic Games?
A. In 1954.
B. In 1964.
C. In 1968.
5. How many Olympic medals did Vietnamese judokas win in 1972?
A. None.
B. One.
C. Two.
Find and correct the mistakes
1. Did Linda went to a pharmacy three days ago?
2. Yesterday, I go to school late because I missed the bus.
3. Lack of exercise may harms your health.
Rewrite the following sentences without changing its meaning
1. How old are you? (What)
__________________________________________
2. She likes singing more than dancing. (prefers)
__________________________________________
3. James isn’t a fast swimmer. (doesn’t)
__________________________________________
4. She usually does her homework for two hours. (spends)
__________________________________________
Đáp án tiếng Anh lớp 7 giữa học kì 1 số 7
Choose the word with a different way of pronunciation in the underlined part.
|
1. A |
2. C |
3. B |
Fill each blank with the present simple, present continuous or past simple form of the verb in brackets
1. When Tom was a teenager, his hobby was horse riding.
2. Do you know that the sun always rises in the East?
3. Look! Toby is having some fast food again!
4. Trung never watches TV before finishing all his homework.
Choose the best option to complete each sentence
|
1. B |
2. B | 3. A | 4. B | 5. A |
6. B |
Read the passage. Circle the best answer A, B, or C to each of the questions
|
1. B |
2. C | 3. B | 4. B |
5. A |
Find and correct the mistakes
1. went => go
Did Linda go to a pharmacy three days ago?
2. go => went
Yesterday, I went to school late because I missed the bus.
3. harms => harm
Lack of exercise may harms your health.
Rewrite the following sentences without changing its meaning
1. What is your age?
2. She prefers singing to dancing.
3. James doesn’t swim fast.
4. She usually spends two hours doing her homework.
Tải bộ đề thi tiếng Anh lớp 7 giữa học kì 1
[su_button url=”https://docs.google.com/document/d/1K7QPgtdOSFe3rkQeFN29FTgOBLBj5tPuyBoOGvmJNIE/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 MÔN TIẾNG ANH LỚP 7[/su_button]
Xem thêm:
- Cách dùng Have / Has và những lưu ý khi sử dụng trong tiếng Anh
- Mạo từ trong tiếng Anh: Khái niệm, tác dụng, phân loại, cách dùng
- Cách học tiếng Anh cho người mất gốc hiệu quả nhanh chóng nhất
Hy vọng thông qua bộ đề thi tiếng anh lớp 7 giữa học kì 1 do Bamboo School tổng hợp, các bạn đã làm quen được với các dạng câu hỏi và kiến thức thường gặp trong mỗi đề thi. Chúc bạn đạt được điểm cao trong những kỳ thi quan trọng sắp tới!
Tổng hợp 4 bộ đề thi giữa kì 1 văn 8 2022-2023 có đáp án (Tải nhiều nhất)
Làm thế nào để ôn tập có hiệu quả cho kỳ thi giữa kì cũng là thắc mắc chung của nhiều học sinh. Trong bài viết này, hãy cùng Bamboo School tham khảo 4 bộ đề thi giữa kì 1 văn 8 – Trung học cơ sở 2022-2023 có đáp án mới nhất và được tải nhiều nhất. Hy vọng những đề thi này sẽ giúp bạn nắm vững kiến thức trọng tâm và đạt được kết quả cao môn văn 8 trong kỳ thi sắp tới.
Đề thi giữa kì 1 văn 8 số 1
I. ĐỌC – HIỂU: (4,0 điểm)
Đọc kĩ đoạn văn sau và trả lời các câu hỏi:
“Mẹ tôi lấy vạt áo nâu thấm nước mắt cho tôi rồi xốc nách tôi lên xe. Đến bấy giờ tôi mới kịp nhận ra mẹ tôi không còm cõi xơ xác quá như cô tôi nhắc lại lời người họ nội của tôi. Gương mặt mẹ tôi vẫn tươi sáng với đôi mắt trong và nước da mịn, làm nổi bật màu hồng của hai gò má. Hay tại sự sung sướng bỗng được trông nhìn và ôm ấp cái hình hài máu mủ của mình mà mẹ tôi lại tươi đẹp như thuở còn sung túc? Tôi ngồi trên đệm xe, đùi áp đùi mẹ tôi, đầu ngả vào cánh tay mẹ tôi, tôi thấy những cảm giác ấm áp đã bao lâu mất đi bỗng lại mơn man khắp da thịt. Hơi quần áo mẹ tôi và những hơi thở ở khuôn miệng xinh xắn nhai trầu phả ra lúc đó thơm tho lạ thường”.
(Ngữ văn 8, tập một)
Câu 1: Đoạn văn trên được trích trong văn bản nào? Tác giả là ai? (1,0 điểm)
Câu 2: Nêu nội dung chính của đoạn văn ? (1,0 điểm)
Câu 3: Tìm các từ thuộc trường từ vựng chỉ các bộ phận của cơ thể con người có trong đoạn văn trên? (1,0 điểm)
Câu 4: Trong đoạn văn trên, tác giả đã sử dụng phối kết hợp các phương thức biểu đạt nào? Cho biết tác dụng của chúng? (1,0 điểm)
II. TẬP LÀM VĂN: (6,0 điểm)
Kể về một việc em đã làm khiến bố mẹ rất vui lòng.
Đáp án đề thi giữa kì 1 văn 8 số 1
I. ĐỌC – HIỂU: (4,0 điểm)
Câu 1:
– Đoạn văn trên được trích từ văn bản Trong lòng mẹ (trích Những ngày thơ ấu).
– Tác giả: Nguyên Hồng.
Câu 2: Nội dung chính của đoạn văn: Miêu tả cảm giác sướng cực điểm của bé Hồng khi được gặp lại mẹ.
Câu 3: Các từ thuộc trường từ vựng chỉ “các bộ phận của cơ thể con người” là: Mặt, mắt, da, gò má, đùi, đầu, cánh tay, miệng.
Câu 4 :
– Trong đoạn văn trên, tác giả đã sử dụng kết hợp các phương thức biểu đạt gồm: Tự sư, miêu tả và biểu cảm.
– Tác dụng: Góp phần làm cho đoạn văn trở nên sinh động, sâu sắc, giàu cảm xúc đối với người đọc.
II. TẬP LÀM VĂN: (6,0 điểm)
1. Mở bài: (1,0 điểm) Giới thiệu về việc em đã làm khiến bố mẹ rất vui lòng.
2. Thân bài: (4,0 điểm)
– Hoàn cảnh xảy ra sự việc.
– Kể lại diễn biến sự việc theo trình tự thời gian, không gian nhất định: Có sự việc khởi đầu, sự việc cao trào, đỉnh điểm, và kết thúc. (Cần lưu ý kết hợp các yếu tố miêu tả và biểu cảm)
– Thái độ của bố mẹ về việc làm của em.
– Suy nghĩ của bản thân về việc làm tốt.
3. Kết bài: (1,0 điểm)
– Cảm nhận chung về việc làm của bản thân.
– Liên hệ: Nêu mong ước, hứa hẹn,…
Đề thi giữa kì 1 văn 8 số 2
I. Đọc – Hiểu: (3 điểm)
Đọc đoạn trích sau và trả lời các câu hỏi:
“Tôi trở về ngôi nhà chênh vênh giữa đồi vải thiều này lắng nghe hoa vải nở […].
Giấc ngủ nơi miền đồi đến nhẹ nhàng và dịu ngọt hương hoa. Tôi tỉnh dậy trước bình minh khi tiếng gà gáy vang, vỗ cánh phành phạch nhẩy từ những cành vải xuống. Bước ra sân nhà, phía trước tôi là sắc hoa ngàn ngạt như một dòng sữa chảy dài dưới ánh nắng. Hoa vải đã nở. Từng chùm hoa li ti, hân hoan kết lại với nhau thành dải đăng ten phủ lên khắp đồi cây. Hơi đất đồi sỏi cũng được ướp vào hương hoa vải, hòa quyện vào nhau tạo nên không gian bạt ngàn, trong lành trước những giọt sương còn vương trên nhánh cỏ may… Đừng dại dột chạy nhảy vô tư vào đồi vải bạt ngàn ấy. Với miền hoa của giấc mơ ngào ngạt này, chủ vườn đã gọi đàn ong yêu về thụ phấn cho vải và hút mật. Bao cánh ong vo ve thành bản hợp xướng cổ súy cho những cánh hoa nở rộn rã với đất trời”.
(Trích Về quê vải, Thu Hà, Góc xanh khoảng trời, NXB Văn học, 2013)
Câu 1: Nhân vật “tôi” trong đoạn trích trên “trở về ngôi nhà chênh vênh giữa đồi vải thiều” để làm gì?
Câu 2: Đoạn văn trên có sự kết hợp của những phương thức biểu đạt nào?
Câu 3: Tìm các từ láy có trong đoạn trích và cho biết tác dụng của chúng.
Câu 4: Qua đoạn văn trên, em hiểu gì về tình cảm của tác giả với miền đất được gọi là miền hoa của giấc mơ ngọt ngào?
II. Tập làm văn: (7 điểm)
Câu 1: (2 điểm) Viết đoạn văn nghị luận theo cách quy nạp triển khai câu chủ đề: “Mỗi người cần phải rèn luyện cho mình tính khiêm tốn”.
Câu 2: (5 điểm) Kỷ niệm đẹp nhất của em về tình bạn tuổi học trò.
Đáp án đề thi giữa kì 1 văn 8 số 2
I. Đọc – Hiểu:

Đáp án đề số 2 phần Đọc – Hiểu
II. Tập làm văn:
Đáp án đề số 2 phần Tập làm văn câu 1
Đáp án đề số 2 phần Tập làm văn câu 2
Đề thi giữa kì 1 văn 8 số 3
I. Đọc hiểu văn bản: (3 điểm)
Đọc đoạn trích sau và trả lời các câu hỏi:
… “Không! Cuộc đời chưa hẳn đã đáng buồn, hay vẫn đáng buồn nhưng lại đáng buồn theo một nghĩa khác. Tôi ở nhà binh Tư về được một lúc lâu thì thấy những tiếng nhốn nháo ở bên nhà lão Hạc. Tôi mải mốt chạy sang. Mấy người hàng xóm đến trước tôi đang xôn xao ở trong nhà. Tôi xồng xộc chạy vào. Lão Hạc đang vật vã ở trên giường, đầu tóc rũ rượi, quần áo xộc xệch, hai mắt long sòng sọc. Lão tru tréo, bọt mép sùi ra, khắp người chốc chốc lại bị giật mạnh một cái, nẩy lên. Hai người đàn ông lực lưỡng phải ngồi đè lên người lão. Lão vật vã đến hai giờ đồng hồ rồi mới chết. Cái chết thật là dữ dội. Chẳng ai hiểu lão chết vì bệnh gì mà đau đớn và bất thình lình như vậy. Chỉ có tôi với Binh Tư hiểu. Nhưng nói ra làm gì nữa! Lão Hạc ơi! Lão hãy yên lòng mà nhắm mắt! Lão đừng lo gì cho cái vườn của lão. Tôi sẽ cố giữ gìn cho lão. Đến khi con trai lão về, tôi sẽ trao lại cho hắn và bảo hắn: “Đây là cái vườn mà ông cụ thân sinh ra anh đã cố để lại cho anh trọn vẹn: cụ thà chết chứ không chịu bán đi một sào…”.
(Nam Cao, Lão Hạc, Ngữ văn 8, tập 1)
Câu 1: Xác định các phương thức biểu đạt được sử dụng trong đoạn trích.
Câu 2: Em hãy cho biết nội dung của đoạn trích.
Câu 3: Tìm các từ ngữ miêu tả về cái chết dữ dội của lão Hạc.
Câu 4: Kể tên các đoạn trích/tác phẩm văn học Việt Nam đã học trong chương trình Ngữ văn 8 cùng giai đoạn sáng tác với truyện ngắn Lão Hạc (giai đoạn 1930 – 1945).
II. Làm văn: (7 điểm)
Câu 1: Viết một đoạn văn (khoảng 10 dòng) lý giải nguyên nhân cái chết của Lão Hạc?
Câu 2: Viết một bài văn nêu suy nghĩ của em về chi tiết chiếc lá cuối cùng trong truyện ngắn Chiếc lá cuối cùng
Đáp án đề thi giữa kì 1 văn 8 số 3
I. Đọc hiểu văn bản:
| Câu | Nội dung | Điểm |
|---|---|---|
| 1 | Tự sự, miêu tả, biểu cảm, nghị luận.(Mỗi phương thức cho 0,25 điểm) | 1,0 |
| 2 | Miêu tả cái chết của lão Hạc và tâm tư của ông giáo. | 1,0 |
| 3 | Lão Hạc đang vật vã ở trên giường, đầu tóc rũ rượi, quần áo xộc xệch, hai mắt long sòng sọc; Lão tru tréo, bọt mép sùi ra, khắp người chốc chốc lại bị giật mạnh một cái, nẩy lên; Lão vật vã đến hai giờ đồng hồ rồi mới chết. | 0,5 |
| 4 | Kể tên các văn bản, tác phẩm đã học:- Tôi đi học (Thanh Tịnh)
– Trong lòng mẹ (Những ngày thơ ấu – Nguyên Hồng) – Tức nước vỡ bờ (Tắt đèn – Ngô Tất Tố) (Nêu đủ 3 VB/TP cho 0,5 điểm; nêu 2 VB/TP cho 0,25 điểm. Nêu 1 VB/TP, không nêu hoặc nêu sai thì không cho điểm). |
0,5 |
II. Làm văn:
| Câu | Nội dung | Điểm |
|---|---|---|
| 1 | a. Đảm bảo thể thức của một đoạn vănb. Xác định đúng vấn đề nghị luận
c. Triển khai hợp lí nội dung đoạn văn: Có thể trình bày theo hướng sau: – Tình cảnh nghèo khổ đói rách, túng quẫn đã đẩy Lão Hạc đến cái chết như một hành động tự giải thoát. – Lão đã tự chọn cái chết để bảo toàn căn nhà, đồng tiền, mảnh vườn, đó là những vốn liếng cuối cùng lão để lại cho con. ⇒ Cái chết của Lão Hạc xuất phát từ lòng thương con âm thầm sâu sắc và lòng tự trọng đáng kính của lão. d. Sáng tạo : HS có thể có suy nghĩ riêng về vấn đề nghị luận. e. Chính tả : dùng từ, đặt câu, đảm bảo chuẩn ngữ pháp, ngữ nghĩa TV. (Trong khoảng 10 dòng nên GV chú ý cách triển khai nội dung đoạn văn của HS. Không “đếm ý” cho điểm. HS trình bày theo hướng khác nhưng hợp lý vẫn cho điểm). |
2,0 |
| 2 | a. Đảm bảo cấu trúc của một bài văn tự sự: có đầy đủ Mở bài, Thân bài, Kết bài.
b. Xác định đúng vấn đề nghị luận. c. Triển khai vấn đề: Viết bài văn nghị luận. Có thể trình bày theo hướng sau: – Chiếc lá cụ Bơ-men vẽ trên tường là một kiệt tác. – Chiếc lá là một kiệt tác trước hết bởi nó sinh động và giống như thật. Giống đến mức con mắt họa sĩ của cả Giôn -xi và Xiu đều không phát hiện ra. – Cụ Bơ-men đã vẽ chiếc lá ấy với tất cả tài năng, tâm huyết của cả đời mình. – Chiếc lá được vẽ trong điều kiện thời tiết vô cùng khắc nghiệt. – Cụ Bơ – men đã vẽ nó bởi tình yêu thương tha thiết cụ dành cho Giôn-xi, vẽ bằng tâm hồn, bằng tấm lòng và cả mạng sống của một người nghệ sĩ tâm huyết với nghệ thuật và cuộc đời. – Chiếc lá cuối cùng đã cứu sống được Giôn-xi, nhờ chiếc lá, cô đã khỏi bệnh. – Kiệt tác của cụ Bơ-men đã khẳng định sự phụng sự chân thành của nghệ thuật đến sự sống tuyệt vời của con người. d. Sáng tạo: HS có cách kể chuyện độc đáo, linh hoạt. e. Chính tả: dùng từ, đặt câu, đảm bảo chuẩn ngữ pháp, ngữ nghĩa TV. |
5,0 |
Đề thi giữa kì 1 văn 8 số 4
Câu 1: (2 điểm) Đọc đoạn trích sau và trả lời câu hỏi bên dưới:
“Mặt lão đột nhiên co rúm lại. Những nếp nhăn xô lại với nhau, ép cho nước mắt chảy ra. Cái đầu lão ngoẹo về một bên và cái miệng móm mém của lão mếu như con nít. Lão hu hu khóc…”
a) Đoạn văn trên được trích trong tác phẩm nào? Tác giả là ai? Nêu nội dung chính của đoạn văn.
b) Xác định từ tượng hình, từ tượng thanh được sử dụng trong đoạn trích trên và nêu tác dụng.
Câu 2: (1 điểm) Cho thông tin “An lau nhà’’. Hãy thêm tình thái từ để tạo một câu cầu khiến và môt câu nghi vấn.
Câu 3: (2 điểm) Viết đoạn văn (khoảng 10 câu) theo mô hình diễn dịch với nội dung: Nguyên nhân dẫn tới cái chết của lão Hạc.
Câu 4: (5 điểm) Em hãy nhập vai Xiu trong truyện ngắn “Chiếc lá cuối cùng” của nhà văn O Hen-ri để kể lại quá trình hồi sinh của nhân vật Giôn-xi.
Đáp án đề thi giữa kì 1 văn 8 số 4
Câu 1:
a) Đoạn văn được trích trong tác phẩm Lão Hạc của nhà văn Nam Cao. (0.5điểm)
– Nội dung chính của đoạn văn: Bộ mặt đau khổ, đáng thương của lão Hạc khi bán cậu vàng. (0,5đ)
b) Xác định từ tượng hình, từ tượng thanh. (0,5đ)
– Từ tượng hình: móm mém
– Từ tượng thanh: hu hu
Tác dụng: Các từ tượng hình, tượng thanh làm nổi bật hình ảnh, dáng vẻ của lão Hạc – một lão nông già nua, khắc khổ, đang khóc thương khi lỡ đối xử tệ bạc với cậu vàng. (0,5đ)
Câu 2:
– An lau nhà đi.
– An lau nhà chưa?
Câu 3:
*Yêu cầu kỹ năng: (0,75 điểm )
- Đúng hình thức đoạn văn: Lùi vào đầu dòng, chữ đầu viết hoa, kết thúc xuống dòng. (0,25 điểm)
- Câu chủ đề mang nội dung khái quát, lời lẽ ngắn gọn, đủ hai thành phần chính, đứng ở đầu đoạn văn. (0,25đ)
- Diễn đạt lưu loát, đảm bảo số câu văn quy định. (0,25đ)
*Yêu cầu nội dung: (1,25đ)
- Tình cảnh đói khổ, túng quẫn đã đẩy lão Hạc đến cái chết như một hành động tự giải thoát, trừng phạt bản thân mình của lão Hạc. (0,25đ)
- Cái chết tự nguyện này xuất phát từ lòng thương con âm thầm mà lớn lao, từ lòng tự trọng đáng kính. (0,25đ)
- Cái chết của lão Hạc giúp chúng ta nhận ra cái chế độ thực dân nửa phong kiến thối nát, cái chế độ thiếu tình người, đẩy người dân đặc biệt là nông dân đến bước đường cùng. (0,5đ)
- Qua đây, chúng ta thấy số phận cơ cực, đáng thương của người nông dân nghèo trước Cách mạng tháng 8. (0,25đ)
Câu 4:
a. Về hình thức: (1,0đ)
- HS biết làm một bài văn tự sự kết hợp với miêu tả và biểu cảm.
- Nhập vai Xiu để kể lại (Xưng tôi ngôi thứ 1)
- Bài viết có bố cục chặt chẽ, mạch lạc, có kỹ năng dựng đoạn, liên kết đoạn, hành văn lưu loát, có sự kết hợp hài hòa giữa các yếu tố kể, miêu tả và biểu cảm.
b. Về nội dung: (4,0đ)
1. Mở bài: Giới thiệu được nhân vật tôi – người kể chuyện (chú ý HS nhập vai nhân vật Xiu). Nêu được ND cần kể lại.
2. Thân bài:
* Nhân vật Xiu kể lại quá trình hồi sinh của Giôn- xi.
-
- Xiu giới thiệu về h.c sống và tâm trạng của Giôn-xi khi chờ đợi cái chết.
- Xiu giới thiệu được h.c sống của Giôn-xi. (nghề nghiệp, tuổi tác, đặc biệt đang trong tình trạng bệnh tật và nghèo khó, có cụ Bơ-men là hàng xóm và cùng làm nghề họa sĩ)
- Tâm trạng của Giôn-xi khi chờ đợi cái chết như thế nào (chán nản, thẫn thờ chờ chiếc lá thường xuân cuối cùng rụng nốt thì cô cũng buông xuôi lìa đời)
-
- Xiu kể về tâm trạng của Giôn-xi khi hồi sinh nhờ chiếc lá cuối cùng mà cụ Bơ-men vẽ (Phần này yêu cầu kể chi tiết).
- Khi chiếc lá thường xuân vẫn còn đó trong một đêm mưa tuyết Giôn-xi đã bừng tỉnh và ngắm nhìn nó thật lâu, sau đó cô đã nói với Xiu những gì, cô muốn ăn, làm đẹp và đặc biệt là muốn vẽ: Giôn-xi đã thực sự hồi sinh. Cô đã vượt qua được cái chết, sự sống đã trở lại với Giôn-xi nhờ vào chiếc lá mỏng manh dẻo dai mà chính Giôn-xi đã nhận ra.
- Khi bác sĩ đến và khẳng định bệnh tình của Giôn-xi hoàn toàn vượt qua giai đoạn khó khăn
- Nhân vật tôi (Xiu) kể lại cho Giôn-xi nghe về sự hy sinh thầm lặng của cụ Bơ-men và khẳng định chiếc lá cuối cùng của cụ là một kiệt tác (chú ý các chi tiết miêu tả và biểu cảm trong phần này)
3. Kết bài: Nêu được cảm nghĩ về tình bạn trong sáng, về tình yêu thương, sự hy sinh giữa những con người nghèo khổ.
Tải bộ đề thi giữa kì 1 văn 8 có đáp án
[su_button url=”https://docs.google.com/document/d/1xOunStLRqt_j8n5Wk3I7MewFXu81Y9fnqGS_WwPzW8Y/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 VĂN 8[/su_button]
Xem thêm:
- Lớp 8 có bao nhiêu môn học? Cần bao nhiêu quyển vở, đồ dùng học tập gì?
- Công thức hóa học là gì? Tổng hợp công thức hóa học lớp 8, 9, 10 đầy đủ nhất
- Bộ đề thi giữa kì 1 toán 8 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
Hy vọng bài viết trên đã cung cấp cho các bạn những kiến thức và nội dung trọng tâm trong bộ đề thi giữa kì 1 văn 8. Chúc các bạn gặt hái thành tích cao trong học tập, và đừng quên đón đọc nhiều kiến thức hữu ích khác tại Bamboo School nhé!
Tổng hợp 4 đề thi giữa học kì 1 lớp 4 tiếng việt 2022-2023 có đáp án tải nhiều nhất
Chắc hẳn ở hiện tại, các bạn học sinh đang gấp rút ôn tập cho kỳ thi giữa học kì 1 năm học 2022 – 2023. Trong bài viết này, Bamboo School sẽ giới thiệu bộ đề thi giữa học kì 1 lớp 4 tiếng việt – Tiểu học kèm đáp án chi tiết, được download nhiều nhất. Mời các bạn cùng tham khảo.
Ma trận đề kiểm tra Tiếng Việt giữa học kì 1 lớp 4
Sau đây là ma trận đề thi giữa học kì 1 lớp 4 tiếng việt. Các thầy cô có thể tham khảo và dựa vào đây để biên soạn bộ đề phù hợp với nội dung chương trình giảng dạy.
|
STT |
Chủ đề |
Mức 1 |
Mức 2 |
Mức 3 |
Mức 4 |
Tổng |
|||||
|
TN |
TL | TN | TL | TN | TL | TN |
TL |
||||
|
1 |
Đọc hiểu văn bản |
Số câu |
2 |
1 | 1 | 1 |
5 |
||||
| Câu số |
1, 2 |
3 | 4 | 8 |
|
||||||
|
2 |
Kiến thức Tiếng Việt |
Số câu |
1 |
2 | 1 | 1 |
5 |
||||
| Câu số |
10 |
5;9 | 6 | 7 |
|
||||||
|
Tổng số câu |
3 | 1 | 3 | 1 | 1 | 1 |
10 |
||||
Đề thi giữa học kì 1 lớp 4 tiếng việt số 1
A. KIỂM TRA ĐỌC
I. Đọc thành tiếng (5 điểm): GV kiểm tra đọc từng em.
II. Đọc thầm và làm bài tập (5 điểm): Thời gian: 30 phút
ĐIỀU MONG ƯỚC KÌ DIỆU
Đêm hè nóng nực, hai chị em ngồi hóng mát, giữa màn đêm lúc ấy bỗng có một ngôi sao vụt sáng, rạch qua bầu trời như một nhát kiếm chói lòa. Cậu em giật áo chị và nói:
– Chị ơi, em nghe người ta nói khi thấy sao đổi ngôi, mình mong ước điều gì thì hãy nói lên điều ước ấy. Thế nào cũng linh nghiệm!
Cô bé quay lại dịu dàng hỏi:
– Thế em muốn ước gì?
Nhớ đến bố con ông lão diễn trò ủ rũ bên đường hồi chiều, cậu em thủ thỉ:
– Ước gì… giấy trong thùng của ông lão biến thành tiền thật. Cô chị bèn cầm lấy tay em và nói với giọng đầy cảm động:
– À, chị bảo điều này …
– Gì ạ?
– À … à … không có gì. Chị chỉ nghĩ … ông cụ chắc cần tiền lắm!
Trong trí óc non nớt của cô bé bỗng hiện lên hình ảnh con lợn đất đựng tiền tiết kiệm cô để dành từ một năm nay trong góc tủ. Cô bé muốn dành cho bố con ông lão và cả em mình một niềm vui bất ngờ.
Theo Hồ Phước Quả
Dựa vào nội dung bài đọc, em hãy khoanh tròn chữ cái trước câu trả lời đúng nhất hoặc làm theo yêu cầu bài.
Câu 1: Khi thấy sao đổi ngôi, cậu em đã làm gì?
A. Ngồi hóng mát và giật mình sợ hãi
B. Ngồi hóng mát và thích thú reo lên
C. Giật áo chị, nói với chị điều mình được nghe người ta nói
Câu 2: Cậu bé ước điều gì? Tại sao?
A. Được đi diễn trò vì cậu muốn có tiền giúp đỡ bố con ông lão bớt nghèo khổ
B. Giấy trong thùng của ông lão biến thành tiền thật, vì thương bố con ông
C. Ước bố con ông lão giàu có, vì cậu muốn mọi người đều giàu có
Câu 3: Cô chị đã nghĩ gì trước ước muốn của cậu em trai?
A. Dùng món tiền tiết kiệm của cô để giúp ông lão
B. Tìm cách giúp em trai mình đạt được ước muốn
C. Cảm động trước ước muốn giấy biến thành tiền thật
Câu 4: Theo em, hai chị em trong câu chuyện có phẩm chất gì đáng quý?
A. Thích xem sao đổi ngôi, tin vào những điều kì diệu
B. Thương người, biết mang lại niềm vui cho người khác
C. Tiết kiệm, biết dành dụm để có một khoản tiền
Câu 5: Thành ngữ, tục ngữ nào dưới đây nêu đúng tình cảm và suy nghĩ của hai chị em trong câu chuyện?
A. Thương người như thể thương thân
B. Bán anh em xa, mua láng giềng gần
C. Một giọt máu đào hơn ao nước lã
Câu 6: Các dấu hai chấm được dùng trong câu chuyện có tác dụng gì?
A. Báo hiệu bộ phận câu đứng sau là lời giải thích cho bộ phận đứng trước
B. Có tác dụng liệt kê các sự vật có trong câu
C. Báo hiệu câu đứng sau là lời nói của một nhân vật
Câu 7: Dòng nào dưới đây chỉ gồm các từ láy?
A. Dịu dàng, chói lòa, ủ rũ, nóng nực, lúng túng, non nớt
B. Ủ rũ, năm nay, thủ thỉ, lúng túng, đổi ngôi
C. Dịu dàng, ủ rũ, thủ thỉ, lúng túng, non nớt
Câu 8: Trong câu: “Ước gì… giấy trong thùng của ông lão biến thành tiền thật.” có mấy danh từ là:
A. Hai danh từ. Đó là (…)
B. Ba danh từ. Đó là (…)
C. Bốn danh từ. Đó là (…)
Câu 9: Câu: “Cô bé muốn dành cho bố con ông lão và cả em mình một niềm vui bất ngờ.” thuộc mẫu câu?
A. Ai – làm gì?
B. Ai – thế nào?
C. Ai – là gì?
Câu 10: Dựa vào nội dung bài đọc, hãy viết một câu theo mẫu Ai – là gì? nói về cậu bé hoặc cô chị trong câu chuyện?
B. KIỂM TRA VIẾT
I. Chính tả (5 điểm – 15 phút)
GV đọc cho HS viết bài
Trung thu độc lập
Đêm nay, anh đứng gác ở trại. Trăng ngàn và gió núi bao la khiến lòng anh man mác nghĩ tới trung thu và nghĩ tới các em. Trăng đêm nay soi sáng xuống nước Việt Nam độc lập yêu quý của các em. Trăng sáng mùa thu vằng vặc chiếu khắp thành phố, làng mạc, núi rừng, nơi quê hương thân thiết của các em…
Anh nhìn trăng và nghĩ tới ngày mai…..
II. Tập làm văn (5 điểm – 35 phút)
Em hãy viết một bức thư gửi thầy cô giáo cũ của em để chúc mừng cô nhân ngày Nhà giáo Việt Nam 20 – 11 và kể cho thầy cô nghe về tình hình trường lớp của em.
Đáp án đề thi giữa học kì 1 lớp 4 tiếng việt số 1
A. PHẦN ĐỌC
I. Đọc thành tiếng (5 điểm)
– GV kiểm tra đọc thành tiếng đối với từng HS.
– Nội dung kiểm tra: HS đọc đoạn văn trong các bài tập đọc đã học ở lớp 4 từ tuần 1 đến tuần 9 khoảng 90 tiếng/ phút; sau đó trả lời 1 câu hỏi về nội dung bài đọc do GV nêu.
– GV đánh giá cho điểm dựa vào những yêu cầu sau:
- Đọc đúng tiếng, đúng từ (1 điểm).
- Đọc sai 2 – 4 tiếng (0,5 điểm).
- Đọc sai 5 tiếng trở nên (0 điểm).
- Ngắt nghỉ hơi đúng ở các dấu câu, các cụm từ rõ nghĩa (1 điểm).
- Ngắt nghỉ hơi không đúng từ 2 – 3 chỗ cho (0,5 điểm).
- Ngắt nghỉ hơi không đúng từ 4 chỗ trở lên cho (0 điểm).
- Giọng đọc có biểu cảm cho (1 điểm).
- Giọng đọc chưa thể hiện rõ tính biểu cảm cho (0,5 điểm).
- Giọng đọc không thể hiện tính biểu cảm cho (0 điểm).
- Tốc độ đạt yêu cầu (không quá 1 phút) (1 điểm).
- Đọc quá 1 – 2 phút cho (0,5 điểm).
- Đọc trên 2 phút cho (0 điểm).
- Trả lời đúng ý câu hỏi do GV nêu ra (1 điểm).
- Trả lời chưa đủ ý hoặc diễn đạt chưa rõ ràng (0,5 điểm).
- Trả lời sai hoặc không trả lời được (0 điểm).
II. Đọc hiểu (5 điểm): Gợi ý đánh giá, cho điểm
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Đáp án | C | B | A | B | A | C | C | C | A | |
| Điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm | 0,5 điểm |
Riêng câu 10: HS đặt câu đúng với nội dung yêu cầu: 0,25 đ
- Trình bày câu đúng (đầu câu viết hoa, có dấu chấm cuối câu): 0,25 đ
- Ví dụ: Cậu bé là người tốt bụng, lương thiện.
B. PHẦN VIẾT
I. Chính tả (5 điểm):
– Viết đúng cỡ chữ, đều nét, rõ ràng không sai lỗi chính tả, trình bày đúng đoạn văn: 5 điểm
– Mỗi lỗi chính tả trong bài viết (sai lẫn phụ âm đầu hoặc vần, thanh không viết hoa đúng quy định…) trừ 0,5 điểm. Lỗi sai giống nhau chỉ trừ 1 lần điểm.
– Nếu chữ viết không rõ ràng, sai về độ cao – khoảng cách – kiểu chữ hoặc trình bày bài bẩn… trừ 1 điểm toàn bài chính tả. (Toàn bài trừ không quá 3 điểm)
II. Tập làm văn (5 điểm):
Đảm bảo các yêu cầu sau được 5 điểm:
– Viết được một bức thư có đủ 3 phần: đầu thư, phần chính, phần cuối thư đúng với nội dung yêu cầu của đề bài (2 điểm)
– Viết câu đúng ngữ pháp, dùng từ đúng, không mắc lỗi chính tả: 1đ.
– Thể hiện được tình cảm, lời chúc mừng thầy cô: 0,5đ
– Kể được ước mơ trong sáng: 1đ.
– Chữ viết rõ ràng, trình bày bài sạch sẽ: 0,5đ (Chỉ cho điểm với bài HS hoàn thành)
– Tuỳ theo mức độ sai sót về ý, về diễn đạt và chữ viết, có thể cho các mức điểm từ 4,5; 4; 3,5; 3; 2,5; 2; 1,5; 1. (Nếu bài văn viết mắc từ 4 lỗi chính tả trở lên – không ghi điểm giỏi)
Bài văn viết thư mẫu
Hà Nội, ngày … tháng … năm….
Cô kính mến!
Em chào cô. Em là học sinh cũ của cô bốn năm về trước. Năm nay em lên lớp 4 rồi, nhưng hình ảnh chập chững bước vào lớp 1 được cô dìu dắt dạy bảo em vẫn còn nhớ như in. Ôi, ngày ấy thân thương đối với em biết nhường nào!
Hôm nay, nhân ngày Nhà giáo Việt Nam – ngày mà chúng em có dịp bày tỏ lòng biết ơn sâu sắc của mình đến thầy, cô giáo cũ. Em viết bức thư nhỏ này gởi thăm cô và xin được nhắc lại một vài kỷ niệm về sự săn sóc của cô đối với em cùng các bạn mà có lẽ tất cả chúng em đều không thể nào quên được.
Lời đầu tiên, em kính chúc cô cùng gia đình dồi dào sức khỏe, luôn gặp điều tốt lành.
Cô ạ! Từ khi xa cô, mỗi ngày em thêm hiểu biết, em đã thấy rõ công lao của thầy cô đối với chúng em.
Em còn nhớ rất rõ dáng cô nghiêng bên chồng sách vở cao ngất mỗi khi chấm bài. Em còn nhớ mãi ngày đầu tiên đi học, cô đón em và dẫn đến xếp hàng cùng các bạn lớp 1A. Em như con chim non đứng trên bờ tổ nhìn quãng trời rộng bao la, cánh chim ấy muốn bay cao nhưng còn ngập ngừng e sợ. Cô là người đã chắp cho em đôi cánh để bay lên từ đó. Cũng như em, các bạn lớp 1A đều được cô chăm sóc từ buổi ban đầu. Cô dạy chúng em tập viết, tập vẽ. Cô ân cần sửa cho chúng em từng tư thế ngồi, từng cách cầm bút, giọng đọc, cách đánh vần…Ôi, công lao của cô thật to lớn, chúng em nghĩ rằng phải ra sức học tập mời đền đáp được công ơn ấy.
Cô ơi! Em chỉ có bấy nhiêu lời thăm cô. Một lần nữa, em kính chúc cô dồi dào sức khỏe và hạnh phúc. Em thầm mong có một ngày nào đó em đến thăm cô. Em mãi là học trò ngoan của cô.
Học sinh cũ của cô
Bùi Lan Hương
Đề thi giữa học kì 1 lớp 4 tiếng việt số 2
A. KIỂM TRA ĐỌC (10 điểm)
I. Đọc tiếng (3 điểm)
II. Đọc thầm và làm bài tập (7 điểm)
Đồng tiền vàng
Một hôm vừa bước ra khỏi nhà, tôi gặp một cậu bé chừng mười hai, mười ba tuổi ăn mặc tồi tàn, rách rưới, mặt mũi gầy gò, xanh xao, chìa những bao diêm khẩn khoản nhờ tôi mua giúp. Tôi mở ví tiền ra và chép miệng:
– Rất tiếc là tôi không có xu lẻ.
– Không sao ạ. Ông cứ đưa cho cháu một đồng tiền vàng. Cháu chạy đến hiệu buôn đổi rồi quay lại trả ông ngay.
Tôi nhìn cậu bé và lưỡng lự:
– Thật chứ?
– Thưa ông, cháu không phải là một đứa bé xấu.
Nét mặt của cậu bé cương trực và tự hào tới mức tôi tin và giao cho cậu một đồng tiền vàng.
Vài giờ sau, trở về nhà, tôi ngạc nhiên thấy cậu bé đang đợi mình, diện mạo rất giống cậu bé nợ tiền tôi, nhưng nhỏ hơn vài tuổi, gầy gò, xanh xao hơn và thoáng một nỗi buồn:
– Thưa ông, có phải ông vừa đưa cho anh Rô-be cháu một đồng tiền vàng không ạ ?
Tôi khẽ gật đầu. Cậu bé tiếp:
– Thưa ông, đây là tiền thừa của ông. Anh Rô-be sai cháu mang đến. Anh cháu không thể mang trả ông được vì anh ấy đã bị xe tông, gãy chân, đang phải nằm ở nhà.
Tim tôi se lại. Tôi đã thấy một tâm hồn đẹp trong cậu bé nghèo.
Theo Truyện khuyết danh nước Anh
Dựa vào nội dung bài đọc, hãy thực hiện các yêu cầu sau:
Câu 1. Khoanh vào chữ cái trước câu trả lời đúng:
Cậu bé Rô-be làm nghề gì? (0,5 điểm)
A. Làm nghề bán báo.
B. Làm nghề đánh giày.
C. Làm nghề bán diêm.
D. Làm ăn xin
Câu 2. Tìm những chi tiết miêu tả ngoại hình của Rô-be? (0,5 điểm)
………………………………………………………………………………………………………………
Câu 3. Qua ngoại hình của Rô-be, em có nhận xét gì về hoàn cảnh của cậu ta? (0,5 điểm)
………………………………………………………………………………………………………………
Câu 4. Vì sao Rô-be không quay lại ngay để trả tiền thừa cho người mua diêm? (0,5 điểm)
A. Vì Rô-be không đổi được tiền lẻ.
B. Vì Rô-be không muốn trả lại tiền.
C. Vì Rô-be bị xe tông, gãy chân.
D. Vì Rô-be không tìm được người đã mua diêm.
Câu 5. Qua hành động trả lại tiền thừa cho người khách, em thấy cậu bé Rô-be có điểm gì đáng quý? (1 điểm)
………………………………………………………………………………………………………………………………….
Câu 6. Nếu em là người khách mua diêm của cậu bé Rô-be trong câu chuyện này, em sẽ làm gì khi biết tin cậu bé bị xe tông, gãy chân đang nằm ở nhà? (1 điểm)
………………………………………………………………………………………………………………………………………………………………………………………………………………………………
Câu 7. Khoanh tròn vào chữ cái trước câu trả lời đúng:
Trong các nhóm từ sau,nhóm nào chứa các danh từ? (1 điểm)
A. Hoa hậu, làng xóm, mưa, hạnh phúc
B. Hạnh phúc, cây bàng, hoa hậu, làng xóm
C. Làng xóm, hoa hậu, cây bàng, mưa
D. Quét nhà, lau nhà, rửa chén
Câu 8. Trong các từ sau, từ nào là từ láy: be bé, buồn bực, buôn bán, mênh mông, mệt mỏi: (0,5 điểm)
Từ láy:
………………………………………………………………………………………………………………………………………………………………………….…………………
Câu 9. Em hãy dùng dấu ngoặc kép có tác dụng dùng để nêu ý nghĩa đặc biệt có trong câu sau: (0,5 điểm)
Chỉ trong 10 năm, Bạch Thái Bưởi đã trở thành một bậc anh hùng kinh tế như đánh giá của người cùng thời.
………………………………………………………………………………………………………………………………………………………………………………………………………………………………
Câu 10. Theo em, câu tục ngữ “Môi hở răng lạnh” có nghĩa là gì?
………………………………………………………………………………………………………………………………………………………………………………………………………………………………
B. KIỂM TRA VIẾT: (10 điểm)
I. Chính tả (Nghe – viết) (2 điểm)
Tiếng hát buổi sớm mai
II. Tập làm văn (8 điểm):
Đề bài: Một người thân của em ở xa đang bị ốm, em không đến thăm được, em hãy viết một lá thư để thăm hỏi và động viên người thân đó.
Đáp án đề thi giữa học kì 1 lớp 4 tiếng việt số 2
A. Kiểm tra đọc (10 điểm)
I. Kiểm tra đọc thành tiếng: (3 điểm)
II. Kiểm tra đọc hiểu kết hợp kiểm tra kiến thức Tiếng Việt: (7 điểm)
Câu 1: C
Câu 2: Chi tiết: ăn mặc tồi tàn, rách rưới, mặt mũi gầy gò, xanh xao
Câu 3: Nhận xét: hoàn cảnh của gia đình Rô-be rất nghèo khổ, gặp nhiều khó khăn…
Câu 4: C
Câu 5 : Cậu bé là người thật thà, tự trọng…..
Câu 6: Em sẽ đến thăm, động viên cậu bé. Nếu gia đình đồng ý em sẽ giúp đỡ đưa cậu bé đến bệnh viện để chữa trị…..
Câu 7: C
Câu 8: Từ láy: be bé, mênh mông.
Câu 9: Chỉ trong 10 năm, Bạch Thái Bưởi đã trở thành “một bậc anh hùng kinh tế” như đánh giá của người cùng thời.
Câu 10: Học sinh trả lời theo suy nghĩ của mình có ý đúng là được. Những người thân thích luôn gắn bó mật thiết và ảnh hưởng lẫn nhau.
B. Kiểm tra viết:
1. Chính tả: (2đ)
Tiếng hát buổi sớm mai
Rạng đông mặt trời tỏa những tia nắng dịu dàng xuồng muôn vật. Bên bìa rừng có một bông hoa lạ, năm cánh mịn như nhung. Bông hoa tỏa hương thơm ngát. Quanh nó thấp thoáng những cánh bướm dập dờn. Mặt trời mỉm cười với hoa. Thế là bông hoa cất tiếng hát. Nó hát mãi, hát mãi. Cuối cùng nó hỏi gió xem có thích bài hát đó không.
Gió ngạc nhiên :
– Ơ, chính tôi hát đấy chứ? Tôi đã làm những cánh hoa của bạn đung đưa, tạo thành tiếng kêu lao xao nên bạn cứ tưởng mình hát.
– Chữ viết rõ ràng, viết đúng kiểu chữ, cỡ chữ: trình bày đúng quy định, viết sạch, đẹp
– Viết đúng chính tả: 2đ sai không quá 5 lỗi trừ 1 điểm
2. Tập làm văn: (8đ)
– Viết được bức thư có bố cục rõ ràng:
+) Phần mở bài: (1 điểm)
- Ghi được thời gian, địa điểm, lời thưa gửi
+) Phần thân bài: (4 điểm)
- Nêu được mục đích, lí do viết thư.(1 điểm)
- Thăm hỏi tình hình của người nhận thư (1 điểm)
- Thông báo tình hình của người viết thư (1 điểm)
- Nêu ý kiến trao đổi hoặc bày tỏ tình cảm với người nhận thư (1 điểm)
+) Phần kết bài: (1 điểm)
- Nêu được lời chúc lời cảm ơn, hứa hẹn, chữ kí và tên (1 điểm)
- Về ngữ pháp, cách trình bày, dùng từ (2 điểm)
- Chữ viết đẹp, đúng chính tả; trình bày sạch đẹp, đúng quy định thể hiện qua bài viết (0,5 điểm)
- Sử dụng câu đúng ngữ pháp, dùng từ đúng nghĩa, rõ nghĩa và sử dụng đúng các dấu câu trong bài. (0,5 điểm)
- Bài viết có sự sáng tạo: có sử dụng từ láy hoặc các biện pháp tu từ, so sánh, nhân hóa, có cảm xúc, ý văn rõ ràng, sinh động… (1 điểm)
Bài văn mẫu
Hà Nội, ngày … tháng … năm …
Bà kính yêu!
Hôm qua cháu nghe bố kể mấy hôm nay trời lạnh quá nên bà lại ốm rồi. Vì cháu bận học chưa về thăm bà được nên cháu viết thư thăm bà đây.
Bà ơi! Bà phải đi khám bác sĩ, uống thuốc và ăn nhiều bà nhé! Như thế bà mới mau khỏe được ạ! Dạo này trời lạnh lắm, khi đi chợ, bà phải mặc nhiều áo ấm, quàng khăn và đi tất vào bà nhé! Cháu nghe mẹ nói, buổi sáng trời lạnh uống một tách trà gừng là rất tốt đấy bà ạ, hôm nào về quê cháu nhất định sẽ mua biếu bà. Giá như bây giờ được nghỉ học, cháu sẽ chạy nhanh về với bà, nấu cho bà ăn, rót nước mời bà uống và chăm sóc bà chu đao, được thế chắc bà vui lắm bà nhỉ?
Còn về gia đình cháu thì mọi người vẫn khỏe. Bố mẹ cháu lúc nào cũng bận rộn. Chị em cháu sắp thi học kì nên phải học và làm bài tập nhiều. Cháu sẽ cố gắng đạt được thật nhiều điểm 10 để dành tặng bà, bà nhé!
Bây giờ, cháu phải học bài rồi. Cuối thư, cháu mong bà nhanh khỏe để còn mời bà lên nhà cháu chơi nữa. Cháu hứa sẽ học tập chăm chỉ, ngoan, nghe lời dạy của bà, của bố mẹ. Cháu sẽ về thăm bà vào một ngày sớm nhất.
Cháu của bà
Khánh Ly
Đề thi giữa học kì 1 lớp 4 tiếng việt số 3
A. KIỂM TRA ĐỌC (10 điểm)
1. Kiểm tra đọc thành tiếng (3 điểm)
2. Kiểm tra đọc hiểu kết hợp kiểm tra kiến thức Tiếng Việt (7 điểm) (35 phút)
Đọc bài sau và trả lời câu hỏi:
Cây sồi và cây sậy
Trong khu rừng nọ có một cây sồi cao lớn sừng sững đứng ngay bên bờ một dòng sông. Hằng ngày, nó khinh khỉnh nhìn đám sậy bé nhỏ, yếu ớt, thấp chùn dưới chân mình.
Một hôm, trời bỗng nổi trận cuồng phong dữ dội. Cây sồi bị bão thổi bật gốc, đổ xuống sông. Nó bị cuốn theo dòng nước đỏ ngầu phù sa. Thấy những cây sậy vẫn tươi xanh hiên ngang đứng trên bờ, mặc cho gió mưa đảo điên. Quá đỗi ngạc nhiên, cây sồi bèn cất tiếng hỏi:
– Anh sậy ơi, sao anh nhỏ bé, yếu ớt thế kia mà không bị bão thổi đổ? Còn tôi to lớn thế này lại bị bật cả gốc, bị cuốn trôi theo dòng nước?
Cây sậy trả lời:
– Tuy anh cao lớn nhưng đứng một mình. Tôi tuy nhỏ bé, yếu ớt nhưng luôn luôn có bạn bè đứng bên cạnh tôi. Chúng tôi dựa vào nhau để chống lại gió bão, nên gió bão dù mạnh tới đâu cũng chẳng thể thổi đổ được chúng tôi.
Nghe vậy, cây sồi ngậm ngùi, xấu hổ. Nó không còn dám coi thường cây sậy bé nhỏ yếu ớt nữa.
Theo Truyện ngụ ngôn nước ngoài
Khoanh tròn vào chữ cái trước ý trả lời đúng nhất cho mỗi câu sau:
1. Tại sao cây sồi xem thường cây sậy? (0,5 điểm)
A. Vì sồi thấy mình vĩ đại.
B. Vì sồi cậy mình cao to còn sậy nhỏ bé, yếu ớt.
C. Vì sồi trên bờ còn sậy dưới nước.
D. Vì sồi thấy mình quan trọng hơn sậy.
2. Dựa vào bài tập đọc, khoanh vào “Đúng” hoặc “Sai” (0,5 điểm)
|
Thông tin |
Trả lời |
| A. Cây sồi sống thân thiện với đám cây sậy. |
Đúng / Sai |
| B. Cây sậy nhỏ bé nên mới không bị bão thổi đổ . |
Đúng / Sai |
3. Cây sồi ngạc nhiên vì điều gì? (0.5 điểm)
A. Cây sậy vẫn xanh tươi, hiên ngang đứng thẳng mặc cho mưa bão
B. Sậy bị bão thổi đổ xuống sông, còn sồi không bị gì.
C. Cây sồi bị cuốn trôi theo dòng nước đỏ ngầu phù sa.
D. Sậy cũng bị cuốn theo dòng nước.
4. Tại sao cây sồi ngậm ngùi xấu hổ, không dám coi thường cây sậy nữa? (0.5 điểm)
A. Vì cây sồi bị bão thổi đổ xuống sông, trôi theo dòng nước.
B. Vì cây sậy không bị mưa bão thổi đổ cuốn trôi.
C. Vì sồi hiểu được sức mạnh đoàn kết của những cây sậy bé nhỏ.
D. Vì sồi thấy sậy không kiêng nể mình.
5. Nêu nội dung câu chuyện? (1 điểm)
6. Qua câu chuyện “Cây sồi và cây sậy”, em rút ra được bài học gì? (1 điểm)
7. Dòng nào dưới đây gồm các từ láy? (0,5 điểm)
A. sừng sững, khinh khỉnh, ngậm ngùi
B. dữ dội, đảo điên, yếu ớt
C. đảo điên, bé nhỏ, luôn luôn
D. tươi xanh, đảo điên, luôn luôn.
8. Câu: “Cây sồi bị bão thổi bật gốc, đổ xuống sông” danh từ là? (1 điểm)
9. Các dấu hai chấm trong câu chuyện trên có tác dụng gì? (0,5 điểm)
A. Báo hiệu bộ phận câu đứng sau là lời giải thích
B. Báo hiệu bộ phận câu đứng sau là phần trích dẫn.
C. Báo hiệu bộ phận đứng sau là lời nói của nhân vật
D. Báo hiệu việc liệt kê sau nó.
10. Tìm từ đơn và từ phức trong câu văn sau: (1 điểm)
Trời bỗng nổi trận cuồng phong dữ dội
B. Kiểm tra viết
1. Chính tả: Nghe – viết bài: “Người ăn xin” – Từ “Lúc ấy … nhường nào”. (Sách Tiếng Việt 4 tập 1, trang 30) (2 điểm)
2. Tập làm văn: Hãy viết một bức thư gửi người thân (người bạn) ở xa để thăm hỏi và kể về tình hình học tập của em trong nửa học kỳ I vừa qua. (8 điểm)
Đáp án đề thi giữa học kì 1 lớp 4 tiếng việt số 3
A. Kiểm tra đọc hiểu: (10 điểm)
1. Kiểm tra đọc thành tiếng (3 điểm)
– Nội dung kiểm tra: Các bài đã học từ tuần 1 đến tuần 9.
– Hình thức:
- Giáo viên ghi tên bài, số trang và câu hỏi vào phiếu.
- Gọi học sinh lên bốc thăm và về chuẩn bị trong khoảng 2 phút.
- Giáo viên kiểm tra đọc thành tiếng đối với từng học sinh. Mỗi học sinh đọc một đoạn văn, thơ khoảng 75 tiếng/phút (trong bài bốc thăm được) sau đó trả lời một câu hỏi về nội dung đoạn đọc đã nêu trong phiếu.
– Đánh giá, cho điểm. Giáo viên đánh giá, cho điểm dựa vào những yêu cầu sau:
a. Đọc vừa đủ nghe, rõ ràng; tốc độ đọc đạt yêu cầu (không quá 1 phút): 1 điểm
b. Đọc đúng tiếng, đúng từ, trôi chảy, lưu loát, ngắt nghỉ đúng: 1 điểm
c. Trả lời đúng câu hỏi về nội dung đoạn đọc: 1 điểm
(Trả lời chưa đầy đủ hoặc diễn đạt chưa rõ ràng: 0,5 điểm; trả lời sai hoặc không trả lời được: 0 điểm)
– Lưu ý: Đối với những bài tập đọc thuộc thể thơ có yêu cầu học thuộc lòng, giáo viên cho học sinh đọc thuộc lòng theo yêu cầu.
2. Kiểm tra đọc hiểu: (7 điểm)
Câu 1: B (0,5 điểm)
Câu 2: A. Sai (0,25 điểm) B. Sai (0,25 điểm)
Câu 3: A (0,5 điểm)
Câu 4: C (0,5 điểm)
Câu 5: (1 điểm) Nội dung câu chuyện: Câu chuyện kể lại chuyện cây sồi to lớn coi thường đám cây sậy nhỏ bé, yếu ớt. Nhưng khi gặp dông bão cây sồi lại bị quật đổ xuống sống. Không nên coi thường người khác
Câu 6: (1 điểm) HS có thể viết: Em không nên coi thường người khác.
- Đoàn kết là sức mạnh giúp chiến thắng những thử thách to lớn.
- Không nên coi thường những người bé nhỏ, yếu đuối hơn chúng ta.
Câu 7: A (0,5 điểm)
Câu 8: (1 điểm) Danh từ là: Cây sồi, bão, gốc, sông.
Câu 9: C (0,5 điểm)
Câu 10: (1 điểm)
Từ đơn: trời, bỗng, nổi, trận (0,5 điểm)
Từ phức: cuồng phong, dữ dội (0,5 điểm)
B – Kiểm tra viết: (10 điểm)
1. Chính tả nghe – viết: (2 điểm) (15 phút)
– GV đọc cho HS viết, thời gian HS viết bài khoảng 15 phút.
– Đánh giá, cho điểm: Bài viết không mắc lỗi chính tả, chữ viết rõ ràng, trình bày sạch sẽ và đúng theo đoạn văn (thơ) 2 điểm.
– Học sinh viết mắc từ 2 lỗi chính tả trong bài viết (sai – lẫn phụ âm đầu hoặc vần, thanh; không viết hoa đúng quy định): trừ 0,5 điểm.
Lưu ý: Nếu chữ viết không rõ ràng, sai về độ cao, khoảng cách, kiểu chữ hoặc trình bày bẩn,…bị trừ 0,5 điểm toàn bài.
2. Tập làm văn: (8 điểm) (25 phút)
Đánh giá, cho điểm
– Đảm bảo được các yêu cầu sau, được 8 điểm:
- Học sinh viết được một bài văn thể loại theo yêu cầu của đề (có mở bài, thân bài, kết bài) một cách mạch lạc, có nội dung phù hợp theo yêu cầu của đề bài.
- Viết câu đúng ngữ pháp, dùng từ đúng, không mắc lỗi chính tả.
- Chữ viết rõ ràng, trình bày bài viết sạch đẹp.
– Tùy theo mức độ sai sót về ý, về diễn đạt và chữ viết có thể cho các mức điểm phù hợp với thực tế bài viết.
* Bài đạt điểm 8 khi học sinh có sử dụng ít nhất từ 1 đến 2 biện pháp nghệ thuật trong tả người.
Lưu ý: Học sinh viết bài tùy theo mức độ mà GV cho điểm đúng theo bài làm của học sinh.
Bài tham khảo
Đồng Nai, ngày … tháng … năm …
Tuấn Anh thân mến!
Vậy là học kì 1 đã đi qua một nửa chặng đường rồi. Nhớ đến lời hẹn cùng thi đua học tập với Tuấn hồi khai giảng nên mình viết bức thư này để chia sẻ với cậu. Dạo này cậu vẫn khỏe chứ? Kết quả thi giữa học kì 1 ở chỗ cậu đã có chưa? Trường mình thì các thầy cô vẫn đang chấm bài. Nhưng mình khá tự tin vì cả mấy tuần vừa qua mình đã học rất chăm chỉ đấy. Các thầy cô đều khen mình đã có tiến bộ hơn năm ngoái nhiều. Mình cũng thường xuyên xung phong phát biểu, lên bảng làm bài và chấm vở bài tập, nên có nhiều điểm 9 điểm 10.
Còn Tuấn Anh thì sao? Cậu hãy chia sẻ với mình qua thư tới nhé!
Bạn qua thư
Hùng
Đề thi giữa học kì 1 lớp 4 tiếng việt số 4
A. Kiểm tra kĩ năng đọc và kiến thức Tiếng việt.
Cho văn bản sau:
Thưa chuyện với mẹ
Từ ngày phải nghỉ học, Cương đâm ra nhớ cái lò rèn cạnh trường. Một hôm em ngỏ ý với mẹ:
– Mẹ nói với thầy cho con đi học nghề rèn.
Mẹ Cương đã nghe rõ mồn một lời con, nhưng bà vẫn hỏi lại:
– Con vừa bảo gì?
– Mẹ xin thầy cho con đi làm thợ rèn.
– Ai xui con thế?
Cương cố cắt nghĩa cho mẹ hiểu:
– Thưa mẹ, tự ý con muốn thế. Con thương mẹ vất vả, đã phải nuôi bằng ấy đứa em lại còn phải nuôi con … Con muốn học một nghề để kiếm sống…
Mẹ Cương như đã hiểu lòng con. Bà cảm động, xoa đầu Cương và bảo:
– Con muốn giúp mẹ như thế là phải. Nhưng biết thầy có chịu nghe không? Nhà ta tuy nghèo nhưng dòng dõi quan sang. Không lẽ bây giờ mẹ để con phải làm đầy tớ anh thợ rèn.
Cương thấy nghèn nghẹn ở cổ. Em nắm lấy tay mẹ, thiết tha:
– Mẹ ơi! Người ta ai cũng có một nghề. Làm ruộng hay buôn bán, làm thầy hay làm thợ đều đáng trọng như nhau. Chỉ những ai trộm cắp hay ăn bám mới đáng bị coi thường.
Bất giác, em lại nhớ đến ba người thợ nhễ nhãi mồ hôi mà vui vẻ bên tiếng bễ thổi “phì phào”, tiếng búa con, búa lớn theo nhau đập “cúc cắc” và những tàn lửa đỏ hồng, bắn toé lên như khi đốt cây bông.
Khoanh vào chữ cái trước câu trả lời đúng từ câu 1 đến câu 6
Câu 1: (0,5 điểm) Cương xin mẹ đi học nghề gì?
a. Nghề thợ xây
b. Nghề thợ mộc
c. Nghề thợ rèn
Câu 2: (0,5 điểm) Cương học nghề thợ rèn để làm gì?
a. Để giúp đỡ mẹ.
b. Để giúp đỡ mẹ, thương mẹ vất vả.
c. Để giúp đỡ mẹ, thương mẹ vất vả, muốn tự kiếm sống.
Câu 3: (0,5 điểm) Mẹ Cương phản ứng như thế nào khi em trình bày ước mơ của mình?
a. Để Cương đi học ngay.
b. Mẹ ngạc nhiên và phản đối.
c. Mẹ Cương phản đối gay gắt.
Câu 5: (0,5 điểm) Nội dung chính của bài này là gì?
a. Cương ước mơ trở thành thợ rèn để kiếm sống.
b. Cương ước mơ trở thành thợ rèn để kiếm sống nên đã thuyết phục mẹ để mẹ thấy nghề nghiệp nào cũng đáng quý.
c. Cương thuyết phục được mẹ và trở thành thợ rèn.
Câu 6: (0,5 điểm) Câu “Bố tôi lái xe đưa ông chủ đi tham dự buổi họp quan trọng.” gồm có mấy từ đơn và từ phức?
a. 5 từ đơn 3 từ phức b. 6 từ đơn 4 từ phức c. 4 từ đơn 5 từ phức
Câu 7: (0,5 điểm) Em tìm 2 danh từ riêng:
………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
Câu 8: (0,5 điểm) Đặt một câu với một danh từ riêng em vừa tìm được:
………………………………………………………………………………………………………………………………………………………………………………………………………………………………….
B. Đọc thành tiếng: (1 điểm).
Đọc đoạn 2 bài: “Bênh vực kẻ yếu” trang 20 sách hướng dẫn học Tiếng việt 4 tập 2A
Đọc đoạn 2 bài: “Trung thu độc lập ” trang 106 sách hướng dẫn học Tiếng việt 4 tập 2A
Đọc 2 khổ thơ đầu bài thơ: “Nếu chúng mình có phép lạ” trang 122 sách hướng dẫn học Tiếng việt 4 tập 2A
Đọc đoạn 1 bài: “Đôi giày ba ta màu xanh” trang 127 sách hướng dẫn học Tiếng việt 4 tập 2A
C. Kiểm tra kĩ năng viết chính tả, viết văn.
I. Chính tả (2 điểm) Nghe – viết
Cây chuối mẹ
Ngày mai, các em có quyền mơ tưởng một cuộc sống tươi đẹp vô cùng. Mươi mười lăm năm nữa thôi, các em sẽ thấy cũng dưới ánh trăng này, dòng thác nước đổ xuống làm chạy máy phát điện; ở giữa biển rộng, cờ đỏ sao vàng phấp phới bay trên những con tàu lớn. Trăng của các em sẽ soi sáng những ống khói nhà máy chi chít, cao thẳm rải trên đồng lúa bát ngát vàng thơm, cùng với nông trường to lớn, vui tươi.
Theo Thép Mới
II. (3 điểm) Tập làm văn
Nhân dịp năm mới, hãy viết thư cho một người thân (ông bà, cha mẹ, thầy cô giáo cũ …) để thăm hỏi và chúc mừng năm mới.
Đáp án đề thi giữa học kì 1 lớp 4 tiếng việt số 4
A. Kiểm tra kĩ năng đọc và kiến thức Tiếng Việt
Câu 7 (0,5 điểm):
Học sinh tìm đủ 2 danh từ riêng cho 0,5 điểm
Câu 8 (0,5 điểm):
Học sinh đặt được câu đúng với 1 danh từ riêng tìm được cho 0,5 điểm.
B. Đọc thành tiếng (1 điểm):
– Học sinh đọc trơn đoạn bài (tốc độ đọc khoảng 40 tiếng/phút), biết ngắt nghỉ hơi đúng sau các dấu câu, đọc hết bài theo quy định ghi 1 điểm
– Học sinh đọc đúng giọng đọc, phát âm còn ngọng, chưa biết ngắt nghỉ hơi đúng ở mỗi dấu câu, tốc độ đọc chưa đảm bảo ghi 0,5 điểm
– Điểm 0,25 là những trường hợp còn lại.
C. Kiểm tra kĩ năng viết chính tả, viết văn
I. Chính tả (2 điểm)
– Học sinh viết đúng toàn bộ nội dung đoạn yêu cầu. Độ cao, khoảng cách giữa các con chữ đúng theo mẫu chữ trong trường tiểu học, trình bày sạch sẽ ghi 2 điểm.
– Học sinh viết đôi chỗ còn chưa đúng các phụ âm, nguyên âm, các dấu thanh khoảng cách các con chữ đều nhau ghi 1 điểm.
– Học sinh viết sai chính tả nhiều, đặt các dấu thanh không đúng quy định ghi 0,5 điểm.
II. Tập làm văn (3 điểm)
– Học sinh viết được bức thư theo yêu cầu bài, đủ bố cục, trình bày sạch sẽ, chữ viết rõ ràng, câu văn đúng cấu trúc ngữ pháp ghi 2 điểm.
– Học sinh viết đúng thể loại, bố cục chưa rõ ràng, còn sai lỗi chính tả chữ viết chưa đẹp ghi 1 điểm.
– Điểm 0,5 là các trường hợp còn lại.
Lưu ý: Học sinh viết đến đâu GV cho điểm đến đó sao cho đúng thực chất.
Tải bộ đề thi giữa học kì 1 lớp 4 tiếng việt có đáp án
Để tải bộ đề thi giữa học kì 1 lớp 4 tiếng việt mới nhất hiện nay kèm đáp án chi tiết, bạn có thể truy cập tại đây:
[su_button url=”https://docs.google.com/document/d/19n8FqafLPlcmyCVdhDXMKth-r2hlJYOrUCB-mhExCTw/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ 1 TIẾNG VIỆT LỚP 4[/su_button]
Xem thêm:
- Tổng hợp đề thi giữa học kì 1 lớp 4 môn Toán có đáp án mới nhất 2022-2023
- Tính từ là gì? Các loại tính từ và cách đặt câu với tính từ trong Tiếng Việt lớp 4
- Từ đồng nghĩa là gì? Tác dụng, phân loại và ví dụ về từ đồng nghĩa
Hy vọng qua bài viết trên, các bạn đã làm quen với ma trận và các dạng đề thi giữa học kì 1 lớp 4 tiếng việt. Chúc các bạn đạt kết quả cao trong các kỳ thi sắp tới.

