Để ôn luyện và làm tốt các bài thi Toán lớp 7, dưới đây là 4 đề thi Toán lớp 7 giữa Học kì 1 năm 2022 – 2023 mà Bamboo School đã tổng hợp từ sách mới Kết nối tri thức, Cánh diều và Chân trời sáng tạo. Cả 4 đề đều sẽ có đáp án và bám sát theo đề thi chính thức Trung học Cơ sở. Hi vọng với bộ đề thi này sẽ giúp các bạn học sinh của chúng ta ôn tập hiểu quả và đạt kết quả cao trong các bài thi sắp tới.
ĐỀ 1
TRẮC NGHIỆM (2 điểm)
Chọn câu trả lời đúng.
Câu 1: Kết quả của phép tính 36.34 là:
- 910
- 324
- 310
- 2748
Câu 2: Từ tỉ lệ thức a/b = c/d (a, b, c, d ≠ 0) ta có thể suy ra:
- d/b = c/a
- a/b = d/c
- a/c = d/b
- a/d = b/c
Câu 3: Cho ba đường thẳng phân biệt a, b, c. Biết a ⊥ c và b ⊥ c, ta suy ra:
- a và b cắt nhau.
- a và b song song nhau.
- a và b trùng nhau.
- a và b vuông góc với nhau.
Câu 4: Nếu 1 đường thẳng cắt 2 đường thẳng song song thì:
- Hai góc trong cùng phía bù nhau.
- Hai góc đồng vị phụ nhau.
- Hai góc so le trong bù nhau.
- Cả 3 ý trên đều sai.
TỰ LUẬN (8 điểm)
Câu 5: (1,5 điểm) Trong các phân số sau đây phân số nào viết được dưới dạng số thập phân hữu hạn, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? Viết dạng thập phân của các phân số đó:
1/4 ; -5/6 ; 13/50
Câu 6: (1,5 điểm) Thực hiện phép tính:
- 2/3 + -1/3 + 7/15
- 3/8.3(1/3)
- (-3)2. (-3)3
Câu 7: (2 điểm) Tìm hai số x và y, biết: x/3 = y/5 và x + y = 16
Câu 8: (1 điểm) Cho đoạn thẳng AB dài 4 cm. Hãy vẽ đường trung trực của đoạn thẳng AB.
Câu 9: (2 điểm) Cho hình vẽ dưới đây. Biết d // d’ và hai góc 700 và 1200.
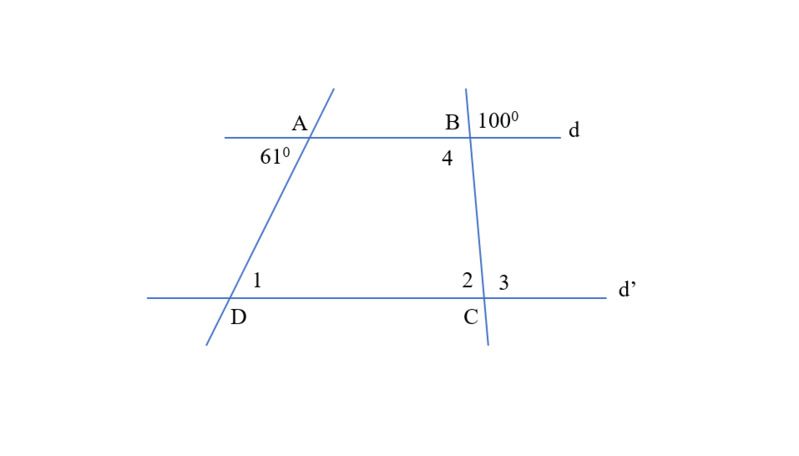
Tính các góc D1; C2; C3; B4.
Đáp án và Hướng dẫn làm bài
I. TRẮC NGHIỆM (2 điểm): Mỗi ý đúng được 0,5 điểm
| Câu | 1 | 2 | 3 | 4 |
| Đáp án | C | A | B | A |
Câu 1.
Ta có: 36.34 = 36+4 = 310
Chọn đáp án C
Câu 2.
Từ tỉ lệ thức a/b = c/d (a, b, c, d ≠ 0)
Suy ra a/c = b/d; b/a = d/c; c/a = d/b
Chọn đáp án A
Câu 3.
Ta có: a ⊥ c; b ⊥ c thì a // b
Chọn đáp án B
Câu 4.
Nếu 1 đường thẳng cắt hai đường thẳng song song thì:
- Hai góc so le trong bằng nhau
- Hai góc đồng vị bằng nhau
- Hai góc trong cùng phía bù nhau
Chọn đáp án A
II. TỰ LUẬN
Câu 5. 1,5 điểm – mỗi phân số đúng được 0,5 điểm
Các số 1/4; 13/50 viết được dưới dạng số thập phân hữu hạn vì:
- 4 = 22, mẫu số 4 không có ước nguyên tố nào khác 2 và 5
- 50 = 2.52, mẫu số 50 không có ước nguyên tố nào khác 2 và 5
- 1/4 = 0,25; 13/50 = 0,26 (thực hiện phép chia)
Còn số -5/6 được dưới dạng số thập phân vô hạn tuần hoàn vì:
- 6 = 2.3, mẫu số 6 có ước nguyên tố 3 khác 2 và 5
- -5/6 = -0,8(3) (Thực hiện phép chia)
Câu 6.
- 2/3 + -1/3 + 7/15 = 10/15 + -5/15 + 7/15 = 12/15 = 4/5 (0,5 điểm)
- 3/8.3(1/3) = (3/8).(10/3) = 10/8 = 5/4 (0,5 điểm)
- (-3)2.(-3)3 = (-3)5 (0,5 điểm)
Câu 7.
Theo tính chất của dãy tỉ số bằng nhau ta có: x/3 = y/5 = (x+y)/(3+5) = 16/8 = 2 (1 điểm)
⇒ x = 3. 2 = 6 và y = 5.2 = 10
Vậy x = 6 và y = 10. (1 điểm)
Câu 8.
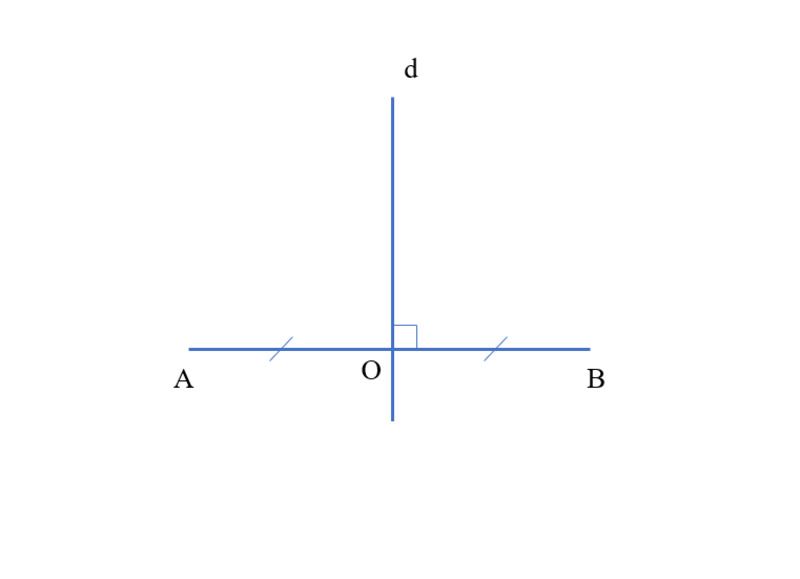
Các bước vẽ:
- Vẽ đoạn thẳng AB dài 4cm.
- Xác định trung điểm O của AB.
- Qua O, vẽ đường thẳng d vuông góc với AB
Khi đó, d là đường trung trực của đoạn thẳng AB.
(Vẽ hình đúng, nêu cách vẽ 1 điểm)
Câu 9.

Ta có: d’//d
⇒ ∠D1 = ∠A = 610 (hai góc so le trong);
∠C2 = ∠B = 1000 (hai góc đồng vị)
Vì ∠C2 + ∠C3 = 1800 (hai kề bù)
⇒ 1000 + ∠C3 = 1800
⇒ ∠C3 = 1800 – 1000 = 800
Ta thấy: ∠B4 = ∠C2 = 1000 (hai góc đối đỉnh)
(Tính đúng mỗi góc 0,5 điểm x 4 = 2 điểm)
ĐỀ 2
TRẮC NGHIỆM (2 điểm)
Chọn câu trả lời đúng.
Câu 1: Kết quả của phép tính (-2/3)2 bằng:
- 2/3
- -2/9
- -4/9
- 4/9
Câu 2: Cho x/6 = 1/2 thì x bằng
- 2
- 3
- -2
- -3
Câu 3. Với a, b, c, d ∈ Z; b, d ≠ 0 kết luận nào sau đây là đúng?
- a/b = c/d = (a+c)/(b-d)
- a/b = c/d = (a-c)/(d-b)
- a/b = c/d = (a-c)/(b-d)
- a/b = c/d = (a-c)/(b+d)
Câu 4. Cho đẳng thức 5.14 = 35.2 ta lập được tỉ lệ thức
- 5/35 = 14/2
- 5/35 = 2/14
- 35/5 = 2/14
- 5/2 = 14/35
Câu 5. Nếu √x = 3 thì x bằng
- 9
- -9
- 3
- -3
Câu 6. Làm tròn số 0,345 đến chữ số thập phân thứ nhất
- A. 0,35
- B. 0,34
- C. 0,3
- D. 0,4
Câu 7. Phân số nào biểu diễn được dưới dạng số thập phân hữu hạn?
- 6/30
- 9/7
- -12/28
- 7/12
Câu 8. Cho hình vẽ dưới đây, ∠BAH và ∠CBE là một cặp góc
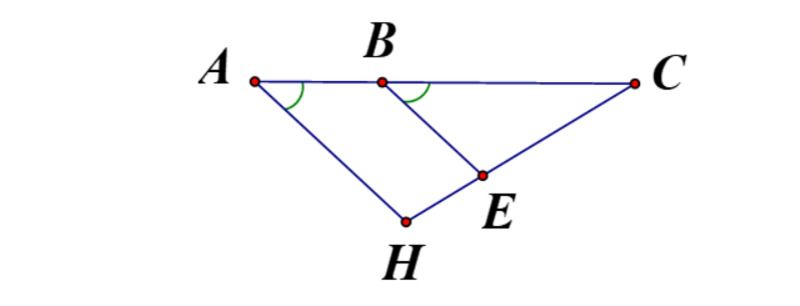
- Bù nhau.
- Trong cùng phía.
- So le trong.
- Đồng vị.
Câu 9. Cho a//b và c⊥a khi đó
- b//c.
- a//c.
- c⊥ b.
- a⊥ b.
Câu 10. Tiên đề Ơ-clít được phát biểu:
“Qua một điểm M nằm ngoài đường thẳng a ….”
- Có duy nhất một đường thẳng đi qua M và song song với a.
- Có hai đường thẳng song song với a.
- Có ít nhất một đường thẳng song song với a.
- Có vô số đường thẳng song song với a.
Câu 11. Cho tam giác ABC. Nhận xét nào dưới đây là đúng?
- ∠A + ∠B + ∠C = 1080
- ∠A + ∠B + ∠C = 1800
- ∠A + ∠B + ∠C < 1800
- ∠A + ∠B + ∠C > 1800
Câu 12. Cho tam giác MHK vuông tại H, thì:
- ∠M + ∠K > 900
- ∠M + ∠K = 1800
- ∠M + ∠K < 900
- ∠M + ∠K = 900
Phần tự luận (7 điểm).
Câu 13. (1,75 điểm) Thực hiện phép tính:
- 8.(-1/2)4
- 5,3.4,7 + (-1,7).5,3 – 5,9
- 2/3 + -1/3 + 7/15
- 40 : {[11 + (26 – 33)].2}
Câu 14. (1,5 điểm) Hưởng ứng phong trào kế hoạch nhỏ của Đội, ba lớp 7A1, 7A2, 7A3 đã thu được tổng cộng 126 kg giấy vụn. Biết rằng số giấy vụn thu được của ba lớp lần lượt tỉ lệ với 6 : 7 : 8. Hãy tính số kg giấy vụn mỗi lớp thu được?
Câu 15. (0,75 điểm) Tìm x, biết:
|x| + 0,25 = 1,75.3
1/3 + x = 2,(60)
Câu 16.( 1,25 điểm) Cho hình vẽ:
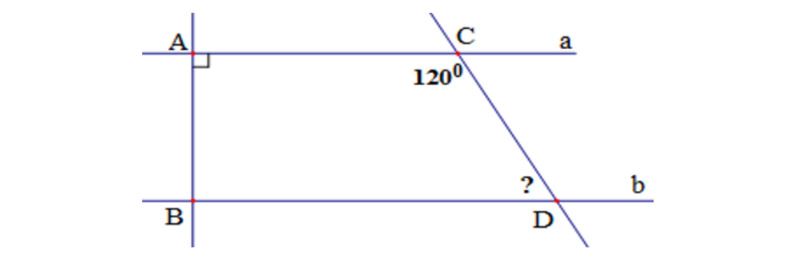
Biết a // b, ∠A = 900, ∠C = 1200
- Đường thẳng b có vuông góc với đường thẳng AB không? Vì sao?
- Tính số đo ∠BCD .
- Vẽ tia phân giác Cx của ∠ACD, tia Cx cắt BD tại I. Tính ∠CID.
Câu 17. (1,75 điểm) Cho tam giác ABC có = 900 và = 200.
- Tính số đo các góc ∠A = 900 và ∠B – ∠C = 200
- Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 1800.
Đáp án và Hướng dẫn làm bài
I. TRẮC NGHIỆM (3 điểm)
Mỗi câu đúng được 0,25 điểm
| CÂU | ĐÁP ÁN | CÂU | ĐÁP ÁN |
| 1 | D | 7 | A |
| 2 | B | 8 | D |
| 3 | C | 9 | C |
| 4 | B | 10 | A |
| 5 | A | 11 | B |
| 6 | C | 12 | D |
Câu 1.
Ta có: (-2/3)2 = (-2)2/32 = 4/9
Chọn đáp án D
Câu 2.
Ta có: x/6 = 1/2
⇒ x.2 = 6.1
⇒ x=3
Chọn đáp án B
Câu 3.
Theo tính chất của dãy tỉ số bằng nhau ta có:
a/b = c/d = (a+c)/(b+d)= (a/c)/(b/d)
Chọn đáp án C
Câu 4.
Từ đẳng thức: 5.14 = 35.2 ta lập được các tỉ lệ thức
5/35 = 2/14; 5/2 = 35/14; 35/5 = 14/2; 2/5 = 14/2
Chọn đáp án B
Câu 5.
Ta có: √x = 3 ⇒ x = 32 = 9
Chọn đáp án A
Câu 6.
0,345 ≈ 0,3 (vì chữ số bỏ đi là 4 < 5)
Chọn đáp án C
Câu 7.
Đưa các phân số đã cho về dạng tối giản và phân tích mẫu:
- 6/30 = 1/5 = 0,2
- -12/28 = -3/7 (mẫu 7 có ước nguyên tố 7 khác 2 và 5)
- 12 = 22.3, nên mẫu số 12 có ước nguyên tố 3 khác 2 và 5
Vậy phân số 6/30 viết được dưới dạng số thập phân hữu hạn.
Chọn đáp án A
Câu 8.

Theo hình vẽ ta thấy ∠BAH và ∠CBE là một cặp góc đồng vị.
Chọn đáp án D
Câu 9.
Ta có: a // b và c ⊥ a thì c ⊥ b (quan hệ giữa tính vuông góc và tính song song).
Chọn đáp án C
Câu 10.
Phát biểu tiên đề Ơclít: “Qua một điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng đi qua M và song song với a.”
Chọn đáp án A
Câu 11.
Theo định lý tổng ba góc trong tam giác ABC ta có: ∠A + ∠B + ∠C = 1800
Chọn đáp án B
Câu 12.
Áp dụng định lý tổng ba góc của tam giác vào tam giác MHK vuông tại H, thì ta có: ∠M + ∠K = 900
(trong tam giác vuông hai góc nhọn phụ nhau).
Chọn đáp án D
II. TỰ LUẬN (7,0 điểm)
Câu 13.
a. 8.(-1/2)4 = 8.(1/16) = 1/2 (0,5 điểm)
b. 5,3.4,7 + (-1,7).5,3 – 5,9
= 5,3(4,7 – 1,7) – 5,9
= 5,3.3 – 5,9
= 15,9 – 5,9 (0,5 điểm)
= 10
c. 2/3 + -1/3 + 7/15 = 10/15 + -5/15 + 7/15
= [10 + (-5) + 7]/15
= 12/15 = 4/5 (0,5 điểm)
d. 40 : {[11 + (26 – 33)].2}
= 40 : {[11 + (26 – 27)].2}
= 40 : {[11 + (-1)].2}
= 40 : (10.2) = 40 : 20 = 2 (0,25 điểm)
Câu 14.
Gọi số kg giấy vụn thu được của 3 lớp 7A1, 7A2, 7A3 lần lượt là a, b, c.
(a, b, c > 0) (0,25 điểm)
Theo bài ra ta có: a/6 = b/7 = c/8 và a+ b + c = 126 (0,25 điểm)
Theo tính chất dãy tỉ số bằng nhau ta có:
a/6 = b/7 = c/8 = (a+ b + c)/(6 + 7 + 8) = 126/21 = 6 (0,5 điểm)
Suy ra:
- a = 6.6 = 36
- b = 7.6 = 42
- c = 8.6 = 48
Vậy số kg giấy vụn thu được của 3 lớp 7A1, 7A2, 7A3 lần lượt là 36 kg, 42 kg, 48kg. (0,25 điểm)
Câu 15.
a. |x| + 0,25 = 1,75.3
|x|= 5,25 – 0,25
|x|= 5
Suy ra: x = 5 hoặc x = -5 (0,5 điểm)
b. 1/3 + x = 2,(6)
1/3 + x = 2 + 0,(6)
x = 2 + 2/3 – 1/3 = 2 +1/3 = 2(1/3)
Vậy x = 2(1/3)
Câu 16.

a. Ta có: a // b và a ⊥ AB
⇒ b ⊥ AB (quan hệ giữa tính vuông góc và tính song song) (0,5 điểm)
b. Vì a // b nên: ∠ACD + ∠BDC = 1800 (vì hai góc trong cùng phía).
Mà ∠ACD = 1200
Do đó: ∠BDC = 1800 – ∠ACD = 1800 – 1200 = 600 (0,5 điểm)
c. Ta có: ∠ACI = 1/2.∠ACD = 1/2.1200 = 600 (CI là tia phân giác của góc ACD)
Vì a // b nên ∠CID + ∠ACI = 600 (hai góc so le trong). (0,25 điểm)
Câu 17.
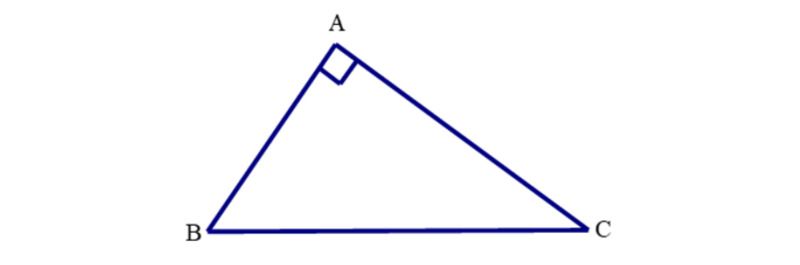
a. Ta có ∠B + ∠C = 900 (hai góc nhọn của tam giác ABC vuông tại A).
Mà ∠B – ∠C = 200
Suy ra: ∠B = (900 + 200) : 2 = 550, ∠C = 900 – 550 = 350 (1 điểm)
b.

Ta có ∠A1 + ∠A2 = 1800 ,
∠B1 + ∠B2 = 1800 ,
∠C1 + ∠C2 = 1800
Do đó: ∠A1 + ∠A2 + ∠B1 + ∠B2 + ∠C1 + ∠C2 = 5400
Mà ∠A2 + ∠B2 + ∠C2 = 1800 (tổng ba góc trong một tam giác ABC)
Nên ∠A1 + ∠B1 + ∠C1 = 3600
Vậy tổng các góc ngoài ở ba đỉnh của một tam giác bằng 1800. (0,75 điểm)
ĐỀ 3
TRẮC NGHIỆM (2 điểm)
Hãy chọn phương án đúng.
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ 1/-2
- -3/5
- 7/-14
- -14/-28
- 7/14
Câu 2: Kết quả của phép tính (-1/2)3 là:
- -3/6
- 1/8
- -3/8
- -1/8
Câu 3: Tỉ lệ thức nào sau đây không thể suy ra từ đẳng thức a.b = c.d
- a/b = c/d;
- a/c = d/b;
- b/c = d/a;
- a/d = c/b.
Câu 4: Cho 3 đường thẳng a, b, c. Biết // và c ⊥ b. Khẳng định nào sau đây là đúng:
- a ⊥ b;
- a và b cùng vông góc với c;
- a // b;
- a và b cùng song song với c.
Tự luận (8 điểm)
Câu 1. (2 điểm) Thực hiện phép tính:
- -12/5 : (-6);
- [8.(1/2)3 + 33].1/9
Câu 2. (1,5 điểm) Tìm x biết:
- (5/2)x – 1/3 = 4/3
- |2x + 0,5| = 8,5
Câu 3. (1,5 điểm)
Một hộp đựng ba loại bi màu khác nhau. Số lượng loại bi màu xanh, bi màu vàng và bi màu đỏ tỉ lệ với các số 5, 7, 9. Tính số bi mỗi loại, biết số bi màu xanh ít hơn số bi màu vàng 4 viên.
Câu 4. (2 điểm) Cho tam giác ABC có ∠A = 900 . Qua đỉnh B của tam giác kẻ đường thẳng xy vuông góc với cạnh AB (AC, By thuộc cùng một nửa mặt phẳng có bờ là đường thẳng chứa cạnh AB).
a) Chứng minh xy // AC.
b) Biết góc ∠CBy = 350 . Tính số đo các góc còn lại của tam giác ABC.
Câu 5. (1 điểm) Tìm x, y biết: (1/3 – 2x)102 + (3y – x)104 = 0
Đáp án và Hướng dẫn làm bài
I. Trắc nghiệm: mỗi câu đúng được 0,5 điểm
| CÂU | 1 | 2 | 3 | 4 |
| ĐÁP ÁN | B | D | A | A |
Câu 1.
Ta có: 7/-14 = 1/-2; -14/-28 = 1/2; 7/14 = 1/2
Vậy phân số 7/-14 biểu diễn số hữu tỉ 1/-2
Chọn đáp án B
Câu 2.
Ta có: (-1/2)3 = -1/8
Chọn đáp án D
Câu 3.
Từ đẳng thức a.b = c.d ta suy ra các tỉ lệ thức sau:
a/c = b/d; a/b = c/d; d/c = b/a; a/b = c/a
Chọn đáp án A
Câu 4.
Ta có: a // c và c ⊥ b thì b ⊥ a (quan hệ giữa tính song song và tính vuông góc)
Chọn đáp án A
II. Tự luận
Câu 1.
a. -12/5 : (-6) = -12/5.(1/-6) = 2/5 (1 điểm)
b. [8.(1/2)3 + 33].1/9 = (8.1/8 +27).1/9 (1 điểm)
= (1+27).1/9 = 28/9
Câu 2.
a. (5/2)x – 1/3 = 4/3
⇒(5/2)x = 4/3 + 1/3
⇒(5/2)x = 5/3
⇒x = 5/3 : 5/2 = 2/3
Vậy x = 2/3 (0,75 điểm)
b. |2x + 0,5| = 8,5
⇒ 2x + 0,5 = 8,5 hoặc 2x + 0,5 = -8,5
⇒ 2x = 8 hoặc 2x = -9
⇒ x = 4 hoặc x = -9/2
Vậy x = 4 hoặc x = -9/2 (0,75 điểm)
Câu 3.
Gọi số bi màu xanh, vàng, đỏ lần lượt là x, y, z (viên) (x, y, z ∈ N*) (0,25 điểm)
Theo bài ra ta có: x/5 = y/7 = z/9 và y – x = 4 (0,5 điểm)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
x/5 = y/7 = z/9 = (y-x)/(7-5) = 4/2 = 2
Suy ra: x = 5.2 = 10
y = 7.2 = 14
z = 9.2 = 18 (0,5 điểm)
Vậy số bi màu xanh, vàng và đỏ lần lượt là 10, 14 và 18 viên. (0,25 điểm)
Câu 4.

| Giả thuyết | ΔABC có ∠A = 900
xy ⊥ AB tại B ∠CBy = 350 |
| Kết luận |
|
Vẽ hình đúng, Ghi GT – KL được (0,5 điểm)
a. Ta có vuông tại A ⇒ AC ⊥ AB (1)
Mà xy ⊥ AB (gt) (2)
Từ (1) và (2) ⇒ xy // AC (quan hệ giữa tính vuông góc và tính song song) (0,75 điểm)
b. Có xy ⊥ AB (gt) ⇒ ∠ABy = 900
Mặt khác ∠ABy = ∠ABC + ∠CBy
⇒ ∠ABC = ∠ABy – ∠CBy = 900 – 350 = 550
Dựa vào tính chất tổng ba góc trong tam giác ABC hoặc từ xy // AC tính được góc ∠ACB = 350 (0,75 điểm)
Câu 5.
Vì (1/3 – 2x)102 ≥ 0 với mọi x;
(3y – x)104 ≥ 0 với mọi x, y. (0,25 điểm)
⇒ (1/3 – 2x)102 + (3y – x)104 = 0
⇔ (1/3 – 2x)102 = 0 và (3y – x)104 = 0 (0,25 điểm)
⇒ 1/3 – 2x = 0 (1) và 3y – x = 0 (2)
Từ (1) suy ra x = 1/6 thay vào (2) ta được:
3y – 1/6 = 0 ⇒ y = 1/18 (0,25 điểm)
Vậy x = 1/6; y = 1/18 (0,25 điểm)
ĐỀ 4
TRẮC NGHIỆM (2 điểm)
Bài 1. Chọn câu trả lời đúng (1 điểm)
Câu 1: Số nào sau đây không phải là số hữu tỉ?
- 0,5
- 1,2(3)
- √2
- 3/-5
Câu 2. Nếu √x = 9 thì x = …..?
- 3
- 18
- ±81
- 81
Câu 3. Cho hình vẽ biết x // y, khi đó hệ thức nào sau đây là không đúng?
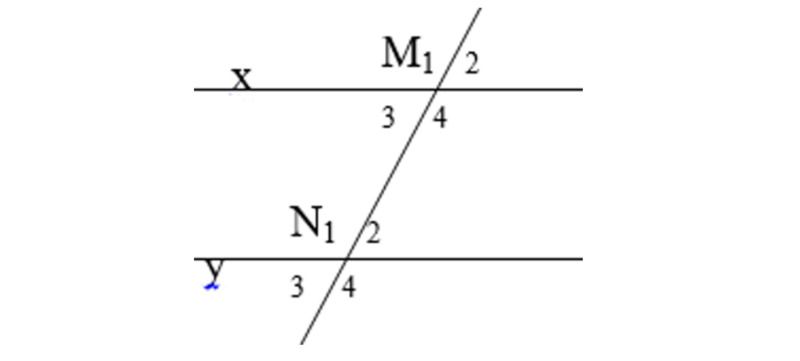
- ∠M1 = ∠N1
- ∠M1 = ∠N3 = 1800
- ∠M3 = ∠N2
- ∠M4 = ∠N3
Câu 4. Nếu ∆ABC = ∆B’A’C’ biết ∠B = 1000 và ∠C = 500 thì khi đó, số đo của ∠A’ là
- 300
- 500
- 1000
- Kết quả khác
Bài 2. Xác định tính đúng – sai của mỗi khẳng định sau (1điểm)
- Chỉ có số 0 không là số hữu tỉ âm và cũng không là số hữu tỉ dương.
- Nếu a ⊥ b và b ⊥ c thì a ⊥ c.
- Số lớn nhất trong 3 số 0,432(32); 0,4(3) và 0,434 là 0,4(3)
- Trong hình vẽ trên (Câu 3) nếu ∠M1 = 1200 và ∠N2 = 600
PHẦN TỰ LUẬN (8 điểm)
Bài 1. (1,5 điểm) Thực hiện phép tính
- 51(1/5.3/8) + 27(1/5.-3/8) + 19
- (-0,75 – 1/4) : (-5) + 1/15 – (-1/5) : (-3)
Bài 2. (1 điểm) Tìm x, biết
- -5/8 + X = (-2/3)2
- |x + 1/3| – 4 = -1
Bài 3. (1,5 điểm) Tam giác ABC có số đo các góc A, B, C tương ứng tỉ lệ với 1:2:3. Tính số đo các góc đó.
Bài 4. (3,5 điểm)Cho DABC có ∠B = ∠C = 400. Từ A, kẻ AH vuông góc với BC tại H. Gọi Ax là tia phân giác góc ngoài đỉnh A:
- Tính số đo ∠BAC
- Chứng tỏ rằng Ax song song với BC
- Chứng tỏ rằng AH vuông góc với Ax
- Chứng tỏ rằng ∠BAH = ∠CAH
Bài 5. (0,5 điểm) So sánh 2603 và 3402.
Đáp án và Hướng dẫn làm bài
I. PHẦN TRẮC NGHIỆM
Mỗi câu đúng được 0,25 điểm x 8 = 2 điểm
| CÂU | 1 | 2 | 3 | 4 | 2a | 2b | 2c | 2d |
| ĐÁP ÁN | C | D | D | C | S | S | S | Đ |
Bài 1.
Câu 1.
Ta có: 0,5 là số thập phân hữu hạn; 1,2(3) là số thập phân vô hạn tuần hoàn với chu kì 3
Do đó các số 0,5; 1,2(3); 3/-5 là số hữu tỉ.
√2 là số vô tỉ vì nó biểu diễn được dưới dạng số thập phân vô hạn tuần hoàn
Chọn đáp án C
Câu 2.
Ta có: √x = 9 ⇒ x = 92 = 81
Chọn đáp án D
Câu 3.

Vì x // y nên
- ∠M1 = ∠N1 (hai góc đồng vị)
- ∠M3 = ∠N1 = 1800 (hai góc trong cùng phía)
Suy ra ∠M1 = ∠N3 = 1800 (Vì ∠M1 = ∠N1; ∠M3 = ∠N3)
- ∠M3 = ∠N2 (hai góc so le trong)
- ∠M4 = ∠N1 (hai góc so le trong)
Mà ∠N1 ≠ ∠N3 nên ∠M4 ≠ ∠N3 nên đáp án D sai
Chọn đáp án D
Câu 4.
Vì ∆ABC = ∆B’A’C’ nên ∠B = ∠A’ (hai góc tương ứng)
Mà ∠B = 1000 nên = ∠A’ = 1000
(Chú ý, đề bài cho số đo góc C để gây nhiễu, đánh lừa)
Chọn đáp án C
Bài 2.
a. Sai, vì số vô tỉ cũng không phải là số hữu tỉ dương và số hữu tỉ âm.
b. Sai, vì a ⊥ b và b ⊥ c thì a // c.
c. Sai
Ta có: 0,432(32) = 0,43232….
0,4(3) = 0,43333…
0,434
Nên 0,432(32) < 0,4(3) < 0,434
Vậy số lớn nhất là 0,434.
d.

Ta có: ∠M1 = ∠M3 = 1800 (hai góc kề bù)
Suy ra ∠M3 = 1800 – ∠M1 = 1800 – 1200 = 600
Vì x // y nên ∠N2 = ∠M3 = 600 (hai góc so le trong)
II. PHẦN TỰ LUẬN
Bài 1.
a. 51(1/5).3/8 + 27(1/5).-3/8 + 19
= 3/8[51(1/5) – 27(1/5)] + 19
= 3/8[(51 – 27) + (1/5 – 1/5)] + 19
= 3/8.24 + 19
= 3.3 + 19 = 28 (0,75 điểm)
b. (-0,75 – 1/4) : (-5) + 1/15 – (-1/5) : (-3)
= (-3/4 – 1/4).-1/5 – (-1/5).-1/3 + 1/15
= (-1).-1/5 – 1/15 +1/15
= 1/5 (0,75 điểm)
Bài 2.
a. -5/8 + x = (-2/3)2
-5/8 + x = 4/9
x = 4/9 – (-5/8)
x = 77/72
Vậy x = 77/72 (0,5 điểm)
b. |x + 1/3| – 4 = -1
|x + 1/3| = -1 + 4
|x + 1/3| = 3
Suy ra x + 1/3 = 3 hoặc x + 1/3 = -3
Suy ra x = 8/3 hoặc x = -10/3
Vậy x = 8/3; x = -10/3 (0,5 điểm)
(Chú ý: Giải đúng, thiếu kết luận trừ 0,25 điểm)
Bài 3.
Theo định lý tổng ba góc trong tam giác ABC ta có: ∠A + ∠B + ∠C = 1800 (0,25 điểm)
Vì số đo ba góc A, B, C tỉ lệ với 1:2:3 nên ta có: ∠A/1 = ∠B/2 = ∠C/3 (0,25 điểm)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
∠A/1 = ∠B/2 = ∠C/3 = (∠A + ∠B + ∠C)/(1 + 2 +3) = 1800/ 6 = 300 (0,25 điểm)
Suy ra ∠A = 300; ∠B = 300.2 = 600; ∠C = 300.3 = 900. (0,25 điểm)
Vậy số đo ba góc A, B, C của tam giác ABC lần lượt là 30°; 60°; 90°. (0,25 điểm)
Bài 4.

| Giả thuyết | ΔABC có ∠B = ∠C = 400
AH ⊥ BC tại H Ax là tia phân giác góc ngoài tại A |
| Kết luận |
|
Ghi đúng GT – KL, vẽ đúng hình 1 điểm
Chứng minh
a. Theo định lý tổng ba góc trong tam giác ABC ta có: = 1800
∠ABC + ∠B + ∠C = 1800
⇒ ∠ABC + 400 + 400 = 1800
⇒ ∠ABC = 1800 – (400 + 400) = 1000 (1 điểm)
b. Gọi Ay là tia đối của tia AC, khi đó góc yAB là góc ngoài tại đỉnh A của tam giác ABC
Theo định lý góc ngoài của tam giác ta có: ∠yAB = ∠B + ∠C = 400 + 400 = 800
Lại có: ∠xAB = 1/2∠yAB = 1/2.800 = 400 (vì Ax là tia phân giác của góc yAB)
Do đó: ∠xAB = ∠B (= 400)
Mà hai góc này ở vị trí so le trong nên Ax // BC. (0,5 điểm)
c. Ta có: AH ⊥ BC (gt) và Ax // BC (câu b)
Do đó: AH ⊥ Ax (quan hệ giữa tính vuông góc và tính song song) (0,5 điểm)
d. Ta có:
∠xAB + ∠BAH = ∠xAH = 900 (AH ⊥ Ax)
Mà ∠xAB = 400 nên ∠BAH = 900 – 400 = 500
Lại có: ∠BAH + ∠CAH = ∠BAC = 1000
Suy ra: ∠CAH = 1000 – 500 = 500
Vậy ∠CAH = ∠BAH (0,5 điểm)
Bài 5.
Ta có: 2603 = 23.201
= (32)201
= 8201 < 9201 = (32)201
= 32.201
= 3402 (0,25 điểm)
Vậy 2603 < 3402 (0,25 điểm)
Tải bộ đề thi giữa kì 1 toán 7 mới nhất có đáp án
[su_button url=”https://docs.google.com/document/d/1pwVT21L1mtxIoXZ5ZHqq8ijHf_wQqihbMTHrxyPj9RE/edit?usp=sharing” target=”blank” background=”#a0e54e” color=”#ffffff” size=”6″]TẢI NGAY BỘ ĐỀ THI GIỮA KÌ TOÁN 7 [/su_button]
Xem thêm:
- Cách giải bài toán bằng cách lập phương trình và các dạng bài thường gặp
- Bộ đề thi giữa kì 1 toán 8 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
- Bộ đề thi giữa kì 1 toán 9 từ cơ bản đến nâng cao có đáp án mới nhất 2022-2023
Trên đây là tổng hợp bộ đề giúp cho các bạn học sinh lớp 7 có thể thêm nguồn tham khảo để luyện tập trước kì thi giữa kì I lớp 7 lần này. Hy vọng bộ đề có thể giúp cho các bạn quen với các dạng bài và có sự chuẩn bị tốt cho kì thi sắp tới. Chúc các bạn học sinh có một kì thi thật tốt









