Cách giải bài toán bằng cách lập phương trình và các dạng bài thường gặp

Hệ phương trình và phương trình đều thuộc vào các dạng kiến thức cơ bản tuy nhiên lại chiếm phần lớn sự quan trọng đối với chương trình môn Toán. Để có hiểu hiểu rõ hơn về các phương pháp lập phương trình và các kiến thức tổng quát nhất trong phương trình, thì sau đây bạn hãy cùng với Bamboo School tìm hiểu về cách giải toán bằng cách lập phương trình và các dạng bài thường gặp nhé!

Tổng quan về phương trình

Trước khi bắt đầu đi sâu vào các phương pháp giải các bài toán qua cách lập phương trình thì chúng ta cần phải thực sự nắm rõ những kiến thức căn bản về phương trình. 

 Phương trình là gì

Thuật ngữ “Phương trình” có ý nghĩa là dùng để nói tới 2 biểu thức bằng nhau. Trong mỗi một phương trình sẽ gồm có biến số hoặc còn gọi là ẩn. Phương trình sẽ gồm có 2 loại sau:

• Phương trình có điều kiện: đây là dạng phương trình sẽ có ý nghĩa duy nhất với một hoặc cùng với một số có giá trị trong biến số. Bên cạnh đó, phương trình có thể không thích hợp với hầu hết các giá trị khác trong biến số.
• Đồng nhất thức: là một dạng phương trình mang ý nghĩa với tất cả các giá trị của biến số.

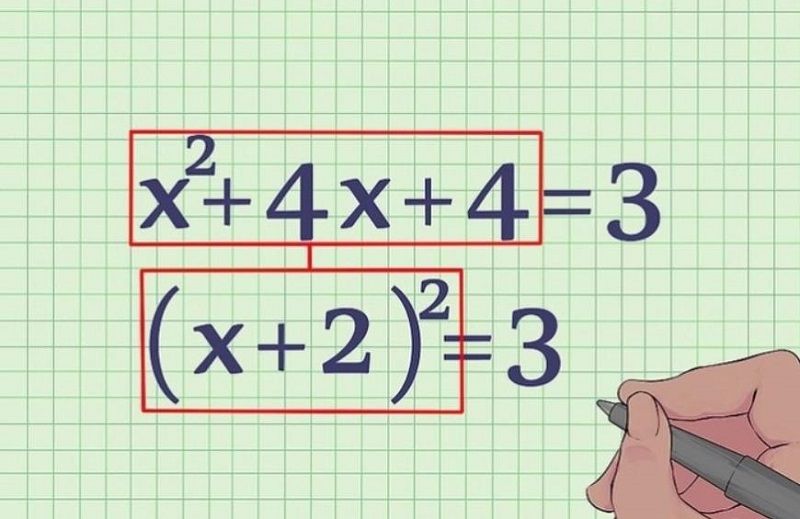
Phương trình cũng như là giải các bài toán bằng cách lập hệ phương trình sẽ là những dạng kiến thức cơ bản nhất để giúp bạn bước đầu tiếp cận dễ dàng những dạng bài tập khác phức tạp hơn thế.

Giải các bài toán bằng cách lập hệ phương trình tức là bạn sẽ cần xác định được chính xác giá trị đúng của những ẩn số để khiến cho phương trình trở nên phù hợp và đúng đắn. Song song đó thì giá trị biến số còn được coi là nghiệm cho phương trình ấy.

Cách trình bày của phương trình là bạn sẽ viết 2 biểu thức ở 2 bên và ở giữa 2 biểu thức sẽ là dấu “=”.

Tác dụng của việc giải bài toán bằng cách phương trình 

Phương trình luôn luôn là một nội dung giảng dạy được xem trọng trong chương trình giáo dục. Việc giảng dạy về cách áp dụng phương trình để giải toán sẽ cho học sinh thấy rõ được sự ứng dụng trong thực tế của những lý thuyết về phương trình đối với đời sống.

Trong cấu trúc của các đề thi quan trọng hàng năm hầu hết luôn có giải các bài toán bằng lập phương trình, ngoài ra các đề thi học sinh giỏi cũng thường gồm có nội dung này để xét chọn, vì vậy mà mỗi học sinh cần chú ý nhiều hơn về việc rèn luyện tốt tới việc phát triển các kỹ năng để có thể giải các bài toán bằng cách lập phương trình.

Giải các bài toán bằng phương trình sẽ vô tình rèn luyện nên các khả năng phân tích tình huống, nghiên cứu các bài toán trong các dạng đặc thù và riêng lẻ. Ngoài ra nếu thực hiện tốt kỹ năng sẽ giúp cho học sinh phát huy tư duy một cách linh hoạt, nhạy bén, sáng tạo cho từng bài toán. Các em sẽ không còn trở nên ngại ngùng khi bắt tay giải các bài toán bằng cách lập phương trình nữa mà sẽ cảm nhận được rằng môn toán thực sự gần gũi với các môn hoặc khác và kể cả đời sống thực tế.

Giải các bài toán bằng cách lập phương trình là một trong các hình thức hữu hiệu để dẫn dắt cho học sinh tự tìm hiểu thêm những nền tảng kiến thức khác. Đây cũng là một cách để vận dụng các kiến thức trên sách vở vào trong thực tế, đời sống hàng ngày. Cũng như đây sẽ là một trong những phương pháp kiểm tra năng lực kiến thức của các bạn học sinh cũng như các khả năng tiếp thu và mức độ vận dụng các kiến thức đã được học.

Các bước giải bài toán bằng cách lập phương trình 

Để có thể giải một bài toán bằng cách lập phương trình không phải là điều quá phức tạp, để có thể nhanh chóng và dễ dàng thực hiện nhất, bạn hãy thực hiện theo 3 bước sau đây:

Bước 1: Phân tích từng chi tiết trong đề bài

Để dễ dàng đưa ra lời giải nhất thì cách tốt nhất là bạn cần phải thật đọc kỹ đề, hiểu và nắm rõ chúng. Qua đó bạn cần xác định những yếu tố sau đây:

• Xem xét các đại lượng đã có sẵn, những đại lượng cần phải tìm và mối quan hệ liên quan giữa 2 loại đại lượng đó.
• Xác định biến số sao cho phù hợp với đề bài cũng như là xác định các điều kiện đối với biến số.
• Thể hiện các đại lượng khác dựa trên biến số đã được chọn.
• Tiến hành lập phương trình.

Bước 2: Bắt đầu giải phương trình

Tiếp theo đây, dựa vào phương trình đã được lập tại bước 1, bạn hãy xác định chính xác các giá trị cần tìm của biến số sao cho phương trình sẽ có ý nghĩa.

Bước 3: Kết luận

Khi bạn đã tìm ra các nghiệm qua các bước trên thì tiếp theo đây bạn hãy so sánh cùng với những điều kiện đã cho sẵn ở phương trình, điều này sẽ giúp bạn tìm ra đáp án chính xác nhất. Sau khi đã có kết quả, hãy tiến hành đưa ra kết luận của bài toán.

Các dạng bài về cách lập phương trình thường gặp

Giải các bài toán bằng các phương pháp lập phương trình là nhóm kiến thức thường hay gặp trong một số các dạng toán về vận tốc, năng suất hay về liên kết hình học hoặc cũng có thể là số học. 

Sau đây là các dạng ghi ví dụ cụ thể dễ hiểu.

Dạng bài về vận tốc 

Đây là dạng bài toán để giúp bạn tính được vận tốc cũng có thể là thời gian hoặc là quãng đường qua các tình huống về phương tiện đang di chuyển. Rèn luyện được giải dạng bài toán này bằng các phương pháp lập phương trình với bài toán vận tốc sẽ hỗ trợ bạn rèn luyện kỹ năng quản lý thời gian.

Công thức của dạng bài toán về vận tốc:

S = v.t

Trong đó:  S nghĩa là quãng đường, v tức là vận tốc, t sẽ là thời gian.

Để có thể bắt đầu tiến hành tính được vận tốc cũng như là khoảng thời gian có thể di chuyển thì bạn cần dựa trên công thức gốc. Và ngoài ra trong các trường hợp cần tính vận tốc của những phương tiện đang di chuyển dưới nước thì bạn sẽ cần phải dựa trên một công thức khác. Nghĩa là:

• v (xuôi) = v (thực) + v (nước)
• v (ngược) = v (thực) – v (nước)

Bài tập ví dụ cụ thể:

Một chiếc ô tô di chuyển từ Tp.Thủ Dầu Một đến thành phố Hồ Chí Minh với vận tốc 45km/h, rồi khi từ Tp.Hồ Chí Minh quay lại Tp.Thủ Dầu Một cùng với vận tốc là 50km/h. Hãy tính quãng đường bắt đầu từ Tp.Hồ Chí Minh cho đến Tp.Thủ Dầu Một? Với thời gian khi về sẽ ít hơn thời gian khi đi 20 phút.

Giải

Dạng bài về năng suất 

Các dạng bài toán về tính năng suất hầu như đều chiếm phần lớn tỷ lệ trong các bài tập giải bằng cách lập phương trình. Công thức về bài toán năng suất như sau: 

V = N.T

Trong đó: V tức là khối lượng công việc thực hiện, N nghĩa là năng suất còn T nghĩa là thời gian.

Để có thể dễ dàng tính được thời gian cần thiết để thực hiện công việc cũng như năng suất thực hiện. Qua việc rèn luyện tính toán tốt năng suất sẽ phần nào giúp bạn có thể quản lý tốt hơn công việc của mình.

Bài tập ví dụ cụ thể:

Một người được cấp trên bàn giao hoàn thiện một lượng sản phẩm trong khoảng thời gian. Người ấy định mỗi ngày sẽ làm xong 48 số lượng sản phẩm. Sau một ngày thực hiện, người ấy nghỉ thêm 1 ngày, vì vậy để có thể hoàn thành công việc đúng tiến độ thì mỗi ngày sau đó cần phải tăng thêm 6 sản phẩm. Vậy dựa trên những dữ liệu có sẵn, hãy tính lượng sản phẩm mà ban đầu người đó đảm nhận.

Giải 

Dạng bài về liên kết hình học 

Những dạng toán có liên quan tới hình học đều sẽ gồm các nội dung về vị trí, kích thước,…Và khi tiến hành giải những bài toán bằng các phương pháp về lập phương trình liên quan đến hình học, thì bạn cần phải chú ý tới một số các công thức khác liên quan tới hình học như tính chu vi hay diện tích,…

Dạng bài về số học

Những bài toán có các nội dung liên quan đến số học đều là các dạng toán có liên quan tới mối quan hệ giữa các số với nhau. Ví dụ như các quan hệ bằng nhau, có thể lớn hơn hoặc là nhỏ hơn hay cũng có thể là các quan hệ đồng dạng hay các quan hệ đồng dư,… Việc bạn tìm ra các ẩn số bằng các phương pháp để giải các bài toán bằng cách lập phương trình sẽ hỗ trợ bạn dễ dàng tìm ra các đáp án cho các biểu thức.

Bài tập ví dụ cụ thể: 

Hai số dương có hiệu bằng 22. Biết rằng số này sẽ gấp đôi so với số kia. Hãy tìm ra hai số dương đó.

Giải:

• Số dương thứ nhất gọi là x ( x>0 )

Số dương thứ hai gọi là y ( y>x>0 )

Vì vậy mà ta có: y-x = 22 suy ra y = 22+x

• Theo như dữ liệu đã cho trước thì số này sẽ gấp đôi so với số kia, ta có:

y = 2x ⇔ 22+x = 2x

⇔ 22 = 2x-x ⇔ x=22 ( thỏa mãn điều kiện)

Với x=22 ⇒  y=44

Vậy ta có thể kết luận rằng, hai số dương thỏa mãn điều kiện nhất là 44 và 22.

Xem thêm:

• Cách tính giá trị biểu thức và ví dụ bài tập minh họa có đáp án
• 10 cách học giỏi toán hiệu quả nhất cho người mất gốc
• R trong toán học là gì? Định nghĩa, tính chất và bài tập minh họa có giải
• Các tính tỉ số phần trăm và các dạng toán về tỉ số phần trăm cơ bản có đáp án

Và trên đây là các cách giải bài toán bằng cách lập phương trình và các dạng bài thường gặp, mong rằng những điều mà Bamboo School chia sẻ tới cho các bạn sẽ hỗ trợ phần nào cho quá trình học tập và rèn luyện của các bạn. Chúc các bạn sẽ ôn tập hiệu quả và gặt hái được kết quả hơn mong đợi.