Trực tâm là gì? Tính chất của trực tâm là kiến thức Toán học quan trọng đối với các em học sinh. Trong bài viết dưới đây, chuyên trang sẽ cùng bạn tìm hiểu về trực tâm là gì, tính chất và cách xác định trực tâm trong tam giác, hãy tiếp tục theo dõi nhé!
Trực tâm là gì?
Trước khi tìm hiểu trực tâm là gì, bạn cần phải biết đến khái niệm đường cao trong tam giác. Đây là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện của tam giác. Cạnh đối diện gọi là đáy, ứng với đường cao.
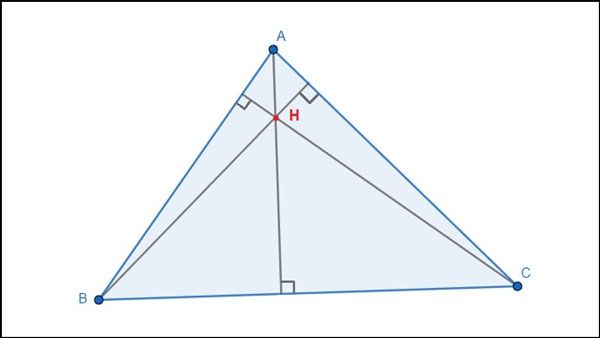
Trực tâm trong tam giác là giao điểm của 3 đường cao
Theo đó, trực tâm của tam giác chính là điểm giao nhau giữa ba đường cao trong tam giác. Trực tâm cũng có những tính chất đặc biệt, mời bạn theo dõi một số tính chất của trực tâm trong tam giác trong phần thông tin tiếp theo.
Tính chất trực tâm tam giác là gì ?
Như bạn cũng đã biết về trực tâm là gì, đây là giao điểm của ba đường cao trong tam giác. Hình ảnh minh họa bên dưới S là trực tâm của tam giác LMN.
Trong một tam giác, trực tâm sẽ có các tính chất sau đây.
Tính chất 1: Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đó đến trung điểm của cạnh nối hai đỉnh còn lại sẽ bằng một nửa khoảng cách từ 1 đỉnh đến trực tâm tam giác.
Tính chất 2: Trong một tam giác cân, đường cao đồng thời là đường trung tuyến, đường phân giác và đường trung trực của đỉnh tam giác đó.
Tính chất 3: Trong tam giác đều, trực tâm đồng thời là trọng tâm, là tâm đường tròn ngoại tiếp và ngoại tiếp tam giác.
Tính chất 3: Đường cao tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ 2 đối xứng của trực tâm qua cạnh tương ứng (Định lý Carnot).
Hệ quả của trực tâm: Trong một tam giác đều, trực tâm, trọng tâm, điểm cách đều ba đỉnh, điểm nằm trong trong tam giác và cách đều ba cạnh là trùng nhau.
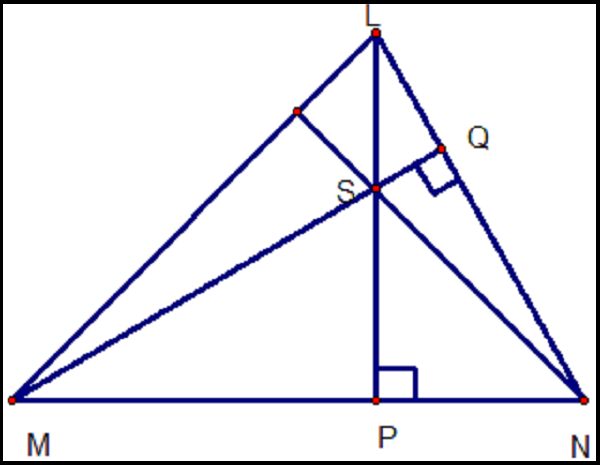
S là trực tâm của tam giác LMN.
Công thức tính trực tâm
Sau khi đã biết trực tâm là gì, các học sinh sẽ có xu hướng tìm kiếm công thức tính trực tâm để giải bài tập nhanh hơn. Tuy nhiên đối với một số trường hợp đặc biệt, bạn có thể áp dụng công thức tính đường cao trong tam giác cân, tam giác đều, tam giác vuông để suy ra kết quả tương ứng.
Cách xác định trực tâm trong tam giác
Khi xác định trực tâm trong tam giác, chúng ta không nhất thiết phải vẽ ba đường cao, bởi khi vẽ hai đường cao trong tam giác là có thể xác định được trực tâm.
Đối với các loại tam giác thông thường như tam giác tù, tam giác nhọn hoặc tam giác đặc biệt như tam giác cân, tam giác đều, cách xác định trực tâm là giống nhau. Từ hai đỉnh của tam giác, ta kẻ đường cao tương ứng đến 2 cạnh đối diện. Điểm giao nhau của hai đường cao đó chính là trực tâm của tam giác và chắc chắn đường cao còn lại cũng đi qua điểm này mặc dù không cần kẻ.
Cách xác định trực tâm tam giác vuông
Cách xác định trực tâm tam giác vuông bằng dấu hiệu nhận biết sẽ giúp bạn dễ xác định hơn. Đối với tam giác vuông, trực tâm chính là đỉnh góc vuông của tam giác đó.
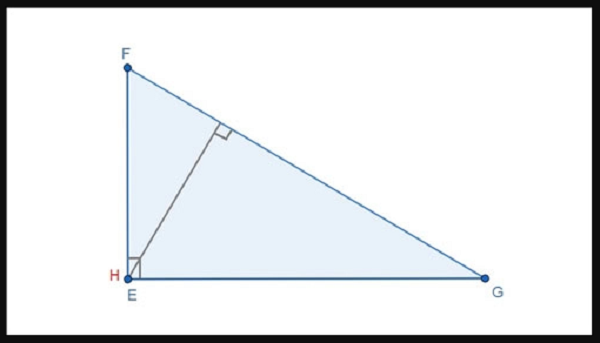
Xác định trực tâm trong tam giác EFG
=> H là trực tâm của tam giác EFG
Cách xác định trực tâm tam giác có góc tù
Đối với tam giác tù, trực tâm nằm ở miền ngoài tâm giác đó.
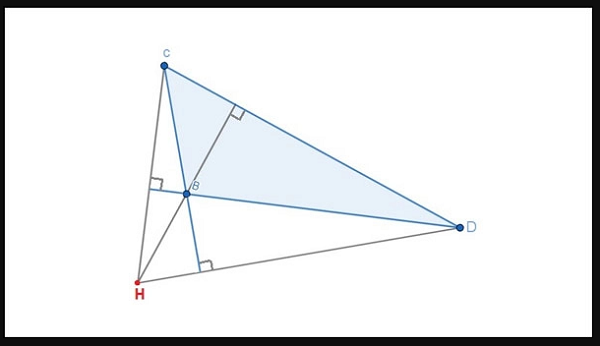
Xác định trực tâm trong tam giác BCD
=> H là trực tâm tâm giác BCD
Cách xác định trực tâm tam nhọn
Đối với tam giác nhọn, trực tâm sẽ nằm ở miền trong tam giác đó.
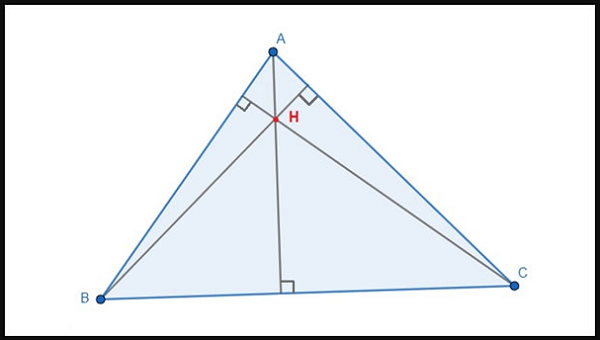
Xác định trực tâm trong tam giác ABC
=> H là trực tâm tam giác ABC
Bài tập về đường trực tâm tam giác
Để giúp bạn hiểu hơn về các tính chất của trực tâm cũng như cách xác định và chứng minh trực tâm trong tam giác, hãy cùng làm các bài tập sau đây:
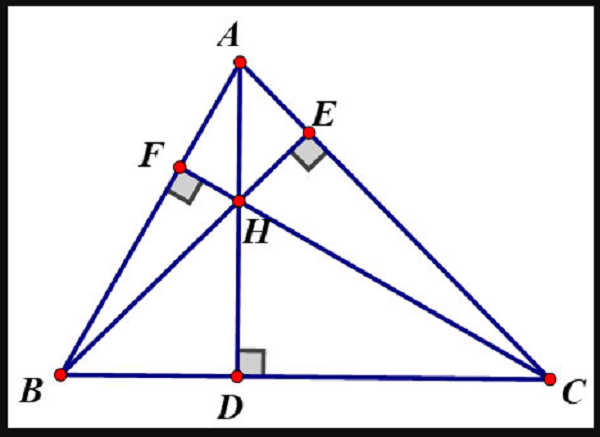
Cho tam giác ABC, gọi H là trực tâm của ABC. Yêu cầu chỉ ra các đường cao của tam giác HBC và chỉ ra trực tâm của tam giác này.
Bài giải:
Gọi D, F, E là chân các đường vuông góc kẻ từ A, C, B của ΔABC.
⇒ AD ⟘ BC, CF ⟘ AB, BE ⟘ AC.
ΔHBC có :
AD ⊥ BC ⇒ AD là đường cao từ H đến BC.
BA ⊥ HC tại F ⇒ BA là đường cao từ B đến HC
CA ⊥ BH tại E ⇒ CA là đường cao từ C đến HB.
AD, BA, CA cắt nhau tại A ⇒ A là trực tâm của ΔHCB.
Xem thêm:
- Công thức tính diện tích tam giác, hình thoi, hình vuông, hình chữ nhật, hình tròn
- Công thức tính chu vi hình vuông, chữ nhật, tam giác, hình tròn, hình thoi
- Các thể thơ trong Văn học Việt Nam được sử dụng phổ biến và thường gặp nhất
Trực tâm luôn là một yếu tố quan trọng trong hình học và đặc biệt quan trọng trong các bài tập liên quan tới hình tam giác. Mong rằng qua bài viết trên, các bạn học sinh cũng nắm vững khái niệm trực tâm là gì và một số tính chất liên quan. Chúc các bạn học thật tốt và đừng quên tham khảo thêm những bài viết khác nhé!









