10+ Cách dạy bé học tiếng anh hiệu quả nhất
Tầm quan trọng của tiếng anh
Trước xu thế hội nhập và toàn cầu hóa như hiện nay thì tiếng anh lại càng đóng vai trò quan trọng hơn nữa. Việc sở hữu vốn ngoại ngữ tốt không chỉ giúp chúng ta phát triển bản thân mà còn mở ra cơ hội việc làm rộng mở trong tương lai. Trau dồi tiếng anh, rèn luyện đầy đủ các kỹ năng nghe – nói – đọc – viết từ sớm sẽ giúp ích cho các bạn trẻ trong mọi lĩnh vực của đời sống.

Việc dạy bé học tiếng anh ngày càng trở nên phổ biến và được các bậc phụ huynh quan tâm
Có nên cho trẻ học tiếng anh từ sớm?
Nhiều người có thắc mắc, liệu có nên dạy bé học tiếng anh từ sớm, và việc đó có thực sự cần thiết hay không. Câu trả lời là có. Ở độ tuổi từ khi còn rất bé, con trẻ có thể hình thành nên thói quen bắt chước, học theo những ngôn ngữ xung quanh mình. Hay nói cách khác, đây còn có thể gọi là Thời kỳ phát cảm về ngôn ngữ. Thường xuyên được tiếp xúc trong môi trường đa ngôn ngữ, được bố mẹ hướng dẫn, dạy về cách đọc, cách phát âm bảng chữ cái,… sẽ giúp trẻ sớm phát triển khả năng giao tiếp của mình.

Trẻ dễ dàng hình thành nên thói quen bắt chước, học theo những ngôn ngữ xung quanh mình
Các cách dạy tiếng anh cho trẻ
Việc dạy bé học tiếng anh thực sự rất quan trọng và mang lại hiệu quả rất lớn. Nhưng làm thế nào để dạy bé học tiếng anh một cách nhanh chóng và có hiệu quả thì không phải phụ huynh, giáo viên nào cũng biết. Dạy học bằng cách đọc – chép truyền thống, ép buộc trẻ phải học thuộc từ vựng không chỉ không giúp trẻ phát triển về khả năng giao tiếp, mà còn có thể khiến trẻ chán nản và sợ việc học.
Sau đây là tổng hợp những cách dạy bé học tiếng anh hiệu quả nhất hiện nay mà bạn có thể tham khảo và áp dụng.
Tạo cho bé niềm vui khi học tiếng anh
Cách đầu tiên trong phương pháp dạy bé học tiếng anh chính là phải tạo được đam mê và niềm vui cho con trẻ. Cách này được áp dụng đối với tất cả các môn học, không riêng gì tiếng anh. Bởi lẽ, chỉ khi có niềm vui và sự hứng thú nhất định thì con trẻ mới có được động lực học tập, tìm tòi thêm về kiến thức.
Bạn không nên ép buộc trẻ phải học theo ý muốn của bạn, mà trước tiên, bạn cần chú ý đến cảm xúc của trẻ. Việc khơi gợi lên niềm vui, sự hứng thú với môn học sẽ giúp bé kích thích sự tò mò, khả năng tư duy đối với ngoại ngữ, từ đó giúp cho việc học tiếng anh trở nên dễ dàng hơn rất nhiều.

Tạo cho bé niềm vui khi học tiếng anh là một điều rất quan trọng
Giữ cho bé thói quen học tiếng anh từ bé
Bước tiếp theo sau khi đã tạo được niềm vui khi học ngoại ngữ của bé chính là tập cho bé thói quen học tiếng anh từ nhỏ. Việc này đòi hỏi sự kiên nhẫn của các bậc phụ huynh và giáo viên, vì học ngoại ngữ đòi hỏi một quá trình rèn luyện lâu dài chứ không phải chỉ là ngày một, ngày hai. Ban đầu, bạn có thể vừa học vừa chơi cùng bé, sau khi bé đã hình thành thói quen học tiếng anh thì sẽ có ý thức tự giác đối với việc học mà không cần đợi sự nhắc nhở từ người lớn.

Bạn nên tập cho bé thói quen học tiếng anh từ sớm
Lồng ghép trò chơi vào bài học
Vừa học vừa chơi luôn là một phương pháp hiệu quả mà bạn có thể thử áp dụng trong khi dạy bé học tiếng anh. Bạn có thể bắt đầu với những trò chơi đơn giản và dễ hiểu như đếm số bằng tiếng anh, đoán từ tiếng anh thông qua hình ảnh, hay là trò chơi liệt kê những từ vựng tiếng anh bắt đầu bằng một chữ cái bất kỳ,…
Có vô vàn những trò chơi đơn giản và thú vị để bạn áp dụng với con trẻ. Bạn có thể tham khảo trên Internet hoặc tự sáng tạo ra những trò chơi của riêng mình.
Bạn có thể lồng ghép trò chơi vào bài học để việc học tiếng anh trở nên sinh động và hấp dẫn hơn
Sử dụng tiếng anh vào một số hoạt động hằng ngày
Nếu học tiếng anh chỉ được rèn luyện từ lý thuyết mà không được thực hành, không được áp dụng vào đời sống thực tiễn thì trẻ sẽ không thể giao tiếp tốt được. Lâu dần, trẻ sẽ quên đi những kiến thức đã được học. Hãy thử gắn liền tiếng anh trong những cuộc đối thoại, giao tiếp hằng ngày với bé. Đây cũng là một cách để bạn “kiểm tra bài cũ” và dạy những kiến thức mới cho bé.

Giao tiếp bằng tiếng anh chỉ thực sự có hiệu quả khi bạn biết hướng dẫn trẻ những mẫu câu cơ bản và dễ hiểu
Cho trẻ xem phim tiếng anh
Xem phim bằng tiếng anh là một trong những lựa chọn hàng đầu của người học ngoại ngữ. Với việc dạy bé học tiếng anh cũng không phải là ngoại lệ. Điều này sẽ giúp cho việc học của bé trở nên sinh động, hấp dẫn và thú vị hơn rất nhiều so với cách học thuộc truyền thống.
Để việc học tiếng anh của bé thực sự có hiệu quả, bạn có thể lựa chọn những bộ phim có nội dung hài hước và thú vị, phim hoạt hình, kèm theo phụ đề tiếng anh chi tiết, dễ hiểu và dễ bắt chước theo cách đọc, cách phát âm của các nhân vật ở trong phim. Trước khi cho bé xem phim, bạn cũng cần kiểm duyệt nội dung phim xem có phù hợp với độ tuổi của bé hay không.
Một số bộ phim hoạt hình bằng tiếng Anh mà bạn có thể cho bé xem khi ở nhà là: Frozen, The lion king, Toy story, Finding Nemo, Kungfu panda,… Với nội dung thú vị, gần gũi và tạo hình nhân vật dễ thương, chắc chắn việc học tiếng Anh của bé sẽ trở nên thú vị và dễ dàng hơn rất nhiều.

Bạn nên cho trẻ xem những bộ phim tiếng anh có nội dung gần gũi, hài hước
Cho trẻ nghe bài hát tiếng anh
Ngoài việc cho con trẻ xem phim tiếng anh thì việc cho trẻ nghe bài hát tiếng anh cũng là một cách rất hiệu quả mà các bậc cha mẹ có thể tham khảo. Những bài hát quen thuộc như đọc bảng chữ cái ABC, đếm số,… sẽ rất phù hợp với độ tuổi của các bé. Bên cạnh đó, giai điệu ngộ nghĩnh, đáng yêu và dễ hát sẽ góp phần kích thích khả năng ghi nhớ và tạo được niềm vui cho bé khi học một ngôn ngữ mới, không phải là tiếng mẹ đẻ.
>>>Xem chi tiết: Những bài hát tiếng anh cho học sinh tiểu học hay, đơn giản, ý nghĩa

Rèn cho trẻ kỹ năng nghe tiếng anh thông qua các bài hát
Đọc truyện bằng tiếng anh cho bé
Những câu chuyện cổ tích chưa bao giờ là lỗi thời đối với con trẻ. Dù là ở độ tuổi nào thì việc đọc truyện bằng tiếng anh cho bé cũng sẽ kích thích khả năng tư duy, trí tưởng tượng phong phú ở trẻ nhỏ. Bạn có thể lựa chọn những câu chuyện về nhân vật đã được nhân hóa, cổ tích, có nội dung gần gũi, thân thuộc và dễ hiểu. Như vậy sẽ giúp cho bé tiếp thu thông tin và kiến thức một cách nhanh chóng và dễ dàng hơn. Thời điểm đọc truyện bằng tiếng anh hiệu quả nhất cho bé là trước khi ngủ.

Bạn có thể đọc truyện bằng tiếng anh cho bé trước khi ngủ
Rèn luyện phát âm cho bé
Đừng chỉ chăm chú vào việc dạy từ vựng, ngữ pháp mà lại quên đi việc tập phát âm cho trẻ nhỏ. Việc trẻ giap tiếp ngoại ngữ có thành thạo hay không cũng phụ thuộc rất lớn vào bước rèn luyện phát âm cho bé. Phương pháp này đòi hỏi bố mẹ và giáo viên phải thật kiên nhẫn khi sửa chi tiết từng lỗi phát âm cho bé.
Bạn có thể cho bé nghe một đoạn hội thoại, một bài hát hay xem một bộ phim bất kỳ,… rồi cho bé bắt chước theo cách nói chuyện của các nhân vật mẫu. Sau đó, bạn cho bé đánh vần, phát âm thật chậm và sửa từng lỗi sai của bé. Lâu dần, khả năng phát âm cũng như giao tiếp của bé sẽ được cải thiện rõ rệt và đáng kể.

Rèn luyện phát âm cho bé đòi hỏi sự kiên nhẫn của các bậc phụ huynh
Giúp bé tự tin giao tiếp
Sau khi đã dạy bé từ vựng, ngữ pháp và cách phát âm, bạn có thể cho bé tập giao tiếp một số mẫu câu đơn giản và luyện tập cho đến khi thành thạo. Hãy gắn liền ngoại ngữ với những tình huống cụ thể trong đời sống như: Cách chào hỏi, giới thiệu bản thân và gia đình, kể về một môn học mà bản thân yêu thích,… Đồng thời, nên rèn luyện cho trẻ sự tự tin, hoạt ngôn và năng động khi giao tiếp tiếng anh trước những người xung quanh.

Rèn cho bé sự tự tin khi giao tiếp bằng tiếng anh
Học qua ứng dụng học tiếng anh
Với sự phát triển và phủ sống rộng rãi của Internet như hiện nay, việc tìm kiếm những tài liệu, ứng dụng học tiếng anh trở nên nhanh chóng và đơn giản hơn rất nhiều. Một số ứng dụng mà bạn có thể cài đặt trên máy tính, điện thoại di động khi dạy bé học tiếng anh là: ELSA Speak, eJoy, Duolingo,… Các ứng dụng này chú trọng giảng dạy về từ vựng, cách phát âm, ngữ pháp, cấu trúc câu,… rất đa dạng và phong phú, thuộc nhiều chủ đề và lĩnh vực khác nhau trong đời sống.
Với giao diện trực quan và sinh động, hình ảnh nhân vật bắt mắt và ngộ nghĩnh, đây là những ứng dụng giúp bé có thể vừa học vừa chơi, ôn luyện kiến thức sau những bài tập, bài kiểm tra và đánh giá năng lực.

Dạy bé học tiếng anh qua ứng dụng là một cách rất hiệu quả
Những mẹo giúp bé học tiếng anh hiệu quả hơn
Để việc dạy bé học tiếng anh có hiệu quả ngay từ sớm, bạn có thể lưu lại một số mẹo dưới đây:
- Kết hợp giữa việc “học mà chơi, chơi mà học” để bé không bị chán nản và sợ học ngoại ngữ
- Thường xuyên áp dụng kiến thức vào đời sống thực tiễn sẽ giúp bé giao tiếp tiếng anh một cách thành thạo và hiệu quả hơn rất nhiều
- Kết hợp linh hoạt giữa nhiều hình thức giảng dạy khác nhau để việc học tiếng anh của bé không trở nên nhàm chán. Bạn có thể kết hợp các hình thức như: Học qua truyền hình, học qua Internet, nghe nhạc có lời, xem phim có phụ đề tiếng anh,…
- Đừng cố gắng nhồi nhét kiến thức, ép buộc trẻ phải ghi nhớ quá nhiều thông tin tiếng anh chỉ trong một thời gian ngắn
- Học và chơi cùng con trẻ
- Thường xuyên cho trẻ tập nói, tập phát âm rồi sửa chi tiết từng lỗi sai của trẻ
- Hãy để bé bắt chước, tập theo cách giao tiếp bằng tiếng anh từ những người xung quanh

Một số mẹo giúp việc dạy bé học tiếng anh đơn giản và hiệu quả hơn
Xem thêm:
- Cách giới thiệu bản thân bằng tiếng anh đơn giản cho học sinh
- Cách học tiếng Anh cho người mất gốc hiệu quả nhanh chóng nhất
- Chương trình tiếng anh Cambridge là gì? Lộ trình học của chương trình Cambridge mới nhất
Hy vọng bài viết trên đã giúp các bạn tham khảo được những cách dạy bé học tiếng anh hiệu quả nhất hiện nay. Mỗi cách dạy đều đem lại những ưu điểm và hiệu quả riêng biệt. Bạn có thể áp dụng linh hoạt nhiều phương pháp khác nhau để cho bé quen thuộc và ghi nhớ mặt chữ, đồng thời hình thành nên khả năng giao tiếp ứng xử bằng ngoại ngữ.
Câu rút gọn là gì? Tác dụng và ví dụ về câu rút gọn
Câu rút gọn là một điểm ngữ pháp được sử dụng rất nhiều trong môn Văn học. Vậy cụ thể thì câu rút gọn là gì? Có bao nhiêu loại câu rút gọn và chúng được dùng ra sao? Bài viết hôm nay sẽ giúp bạn giải đáp các thắc mắc trên! Hãy cùng theo chân BamBoo School đến với chủ đề Câu rút gọn nhé!
Câu rút gọn là gì?
Định nghĩa của câu rút gọn chính là những câu được sử dụng trong văn nói hoặc viết với cấu trúc câu được tinh giản, một số thành phần trong câu có thể được lược bỏ tùy vào ngữ cảnh sử dụng.
Tuy nhiên, việc lược bỏ một số thành phần trong câu đôi lúc sẽ tạo cảm giác cộc lốc, thiếu lịch sự cho người đọc/nghe. Vậy nên bạn hãy cân nhắc tinh giản các thành phần trong câu dựa trên ngữ cảnh sử dụng để tránh gây nên những hiểu lầm không đáng có nhé!

Ví dụ:
Câu hoàn chỉnh: Bài tập hôm qua cô giao cho lớp, An đã làm chưa? – Mình chưa làm.
Câu rút gọn: An làm bài tập cô giao chưa? – Chưa.
Kết luận: bạn An đã rút gọn câu trả lời của mình. Tuy nhiên trong trường hợp này thì câu trả lời có phần cộc lốc gây cảm giác không thoải mái cho người nghe.
Tác dụng câu rút gọn
Câu rút gọn có rất nhiều tác dụng trong đời sống hằng ngày của chúng ta:
- Giúp truyền tải nội dung ngắn gọn, súc tích.
- Tránh việc bị lặp từ, lặp nội dung.
- Với mục tiêu truyền tải nhanh chóng các nội dung, câu rút gọn chính là giải pháp tốt nhất.
- Việc rút gọn và chỉ trình bày các ý chính giúp người nói/viết dễ dàng bày tỏ và nhấn mạnh các ý quan trọng mà mình muốn truyền tải đến người nghe/đọc.
Các loại câu rút gọn
Câu rút gọn chủ ngữ
Trong loại câu này, chủ ngữ sẽ được lược bỏ. Thông thường trong trường hợp này thì cả người nói/viết lẫn người nghe/đọc điều hiểu được rằng họ đang đề cập về chủ thể nào.
Ví dụ:
An: Ngày mai có buổi họp lớp ấy! Có đến không? (Ngày mai có buổi họp lớp ấy! Cậu có đến không?)
Hương: Chưa biết nữa, dạo này hơi bận! (Tớ cũng chưa biết nữa vì dạo này tớ hơi bận!)
Câu rút gọn vị ngữ
Như tên gọi của mình, loại câu rút gọn này sẽ tinh giản thành phần vị ngữ trong câu. Thông thường trong giao tiếp mọi người sẽ sử dụng mẫu câu này rất nhiều vì họ muốn trả lời nội dung chính và tránh lặp lại câu hỏi được hỏi.
Ví dụ:
An: Ngày mai lớp mình ai phụ trách việc trực nhật thế?
Hương: Tớ! (Ngày mai tớ phụ trách việc trực nhất của lớp!)
Câu rút gọn chủ ngữ và vị ngữ
Khi người nói/viết và người nghe/đọc đều hiểu rõ về chủ thể và chủ đề họ đang bàn luận thì họ sẽ dùng câu rút gọn cả chủ lẫn vị.
Ví dụ:
An: Bình thường cậu giành bao nhiêu thời gian để luyện đàn mỗi ngày?
Hương: 2 tiếng. (Mỗi ngày tớ dành 2 tiếng để luyện đàn)
Cách sử dụng câu rút gọn
Như đã được đề cập, bạn cần lưu ý khi sử dụng các câu rút gọn vì trong một số hoàn cảnh thì các loại câu rút gọn sẽ tạo cảm giác khó gần và không thoải mái thậm chí là khiến người nghe cảm thấy bạn không tôn trọng họ.
Sau đây sẽ là một số lưu ý và cách sử dụng câu rút gọn trong đời sống hằng ngày:
- Không nên lạm dụng câu rút gọn, chỉ nên sử dụng đúng lúc, đúng nơi và đúng đối tượng.
- Cần phải đảm bảo truyền tải đầy đủ các thông tin quan trọng và cần thiết đến người nghe.
- Trong văn viết, câu rút gọn không được khuyến khích sử dụng (trừ một số trường hợp đặc biệt).
- Câu rút gọn nên được sử dụng trong giao tiếp hằng ngày giữa các đối tượng đồng trang lứa hoặc nhỏ tuổi hơn bạn (Tránh việc nói trống không với người lớn tuổi hơn).
Phân biệt câu rút gọn và câu đặc biệt
Trong một số hoàn cảnh, mọi người vẫn thường hay nhầm lẫn giữa câu rút gọn và câu đặc biệt. Dựa trên một số các yếu tố nổi bật cùng với cách sử dụng của chúng mà BamBoo School đã thiết lập nên một bảng phân biệt chi tiết sau đây:
| Câu rút gọn | Câu đặc biệt | |
| Cấu tạo | Đầy đủ chủ ngữ, vị ngữ
⇒ Chỉ lược bỏ một số thành phần tùy thuộc vào ngữ cảnh |
Không đầy đủ 2 thành phần chủ -vị |
| Khôi phục thành câu hoàn chỉnh trở lại | Có thể | Không thể |
| Xác định thành phần bị rút gọn | Có thể xác định được nhờ vào ngữ cảnh sử dụng câu | Không thể xác định (Từ – cụm từ trong câu đặc biệt đều là trung tâm chính của câu) |
Bài tập về câu rút gọn
Lấy 5 ví dụ về câu rút gọn
a. An có muốn đi công viên nước với Hương không?
⇒ Đi công viên nước không?
b. Hôm nay bạn đã ăn no chưa?
⇒ No chưa?
c. Sáng ngày mai hai đứa mình cùng đi ăn sáng nha?
⇒ Sáng mai cùng đi ăn sáng nha?
d. Hè này cậu đi du dịch ở đâu vậy? – Tớ đi du lịch ở Hà Nội
⇒ Hè này đi du lịch ở đâu vậy? – Hà Nội.
e. Ngày mai cậu đi học lúc mấy giờ đấy? – 11 giờ tớ sẽ đi.
⇒ Mai đi học lúc mấy giờ đấy? – 11 giờ.
Đặt câu rút gọn
a. Cậu có định tham gia hoạt động 20/11 không? – Không (lược bỏ chủ ngữ)
b. Mẹ đang nấu món gì vậy ạ? – Canh chua (lược bỏ chủ ngữ)
c. Ban cán sự lớp cậu là ai thế? – Hòa và Doanh (lược bỏ vị ngữ)
Cách tìm câu rút gọn
Câu 1: Xác định thành tố bị khuyết và khôi phục các câu rút gọn sau đây
- Đồn rằng quan tướng có danh
- Cưỡi ngựa một mình, chẳng phải vịn ai
- Ban khen rằng “Ấy mới tài”
- Ban cho cái áo với hai đồng tiền
- Đánh giặc thì chạy trước tiên
- Xông vào trận tiền cởi khố giặc ra
- Trở về gọi mẹ mổ gà khao quân
Khôi phục:
- Người ta đồn rằng quan tướng có danh
- Hắn cưỡi ngựa một mình, chẳng phải vịn ai
- Vua ban khen rằng “Ấy mới tài”
- Và ban cho cái áo với hai đồng tiền
- Quan tướng khi Đánh giặc thì chạy trước tiên
- Khi xông vào trận tiền cởi khố giặc ra
- Quan tướng trở về gọi mẹ mổ gà khao quân
Câu 2: Trong các câu sau đây, câu nào là câu rút gọn?
- Người ta là hoa đất.
- Ăn quả nhớ kẻ trồng cây.
- Nuôi lợn ăn cơm nằm, nuôi tằm ăn cơm đứng.
- Tấc đất, tấc vàng.
Hướng dẫn:
- Câu (2) và (3) là câu rút gọn
- Hai câu nên lên nguyên tắc ứng xử chung nhằm răn dạy người đọc vậy nên đã rút gọn đi chủ ngữ trong câu.
Xem thêm:
- Điệp từ là gì? Điệp ngữ là gì? Cấu trúc và ví dụ minh họa
- So sánh là gì? Cấu tạo, phân loại và ví dụ về phép so sánh
- Động từ là gì? Cụm động từ là gì? Cách xác định và đặt câu với động từ
Bên trên là toàn bộ các kiến thức về câu rút gọn cùng với một số bài tập để các bạn học sinh có thể luyện tập! Mong rằng bài viết này mang đến cho các bạn học sinh những kiến thức bổ ích và có thể hỗ trợ các bạn trong quá trình học tập.
Cấu trúc it take, it took và Spend: Cách dùng, đặt câu và bài tập ví dụ có giải
Một trong những cấu trúc thường xuyên được sử dụng nhất trong văn nói và rất hay được bắt gặp trong các đề kiểm tra tiếng Anh đó chính là cấu trúc It take/took và spend. Vậy bạn đã biết đến cấu trúc này trong tiếng Anh chưa? Đừng lo, trong bài viết hôm nay, BamBoo School sẽ mang đến cho bạn tất tần tất các thông tin từ cách dùng, cấu trúc ngữ pháp và cả một số bài tập thực hành nữa. Bảo đảm rằng chỉ sau bài viết này thôi, bạn sẽ hiểu và thông thạo cách sử dụng của 2 loại cấu trúc này!
Cấu trúc It take và cách dùng

Cấu trúc It take cơ bản
Để nói rằng bạn/một người nào đó đã dành bao nhiêu thời gian cho một việc gì đó, ta dùng cấu trúc sau đây
| It take(s) + (time) + to + Verb |
| It take(s) + somebody + (time) + to + Verb |
Ví dụ:
- It takes me 7 years to speak English fluently. (Mất đến 7 năm để tôi có thể nói tiếng Anh trôi chảy)
- It takes Hoang Anh 2 months to play guitar. (Hoàng Anh đã mất 2 tháng để biết chơi đàn ghi-ta)
Cấu trúc đặc biệt khác của It take
Muốn bày tỏ rằng, để hoàn thành một công việc gì đó thì bao nhiêu là cần thiết, ta dùng:
| It takes + (quantity + noun) to + Verb |
Ví dụ:
- It takes us totally $500 to have a day in Disneyland. (Mất tổng cộng 500 đô-la để chúng tôi có một ngày vui chơi ở Disneyland)
Cách viết lại câu với It take
Để không phải lặp lại một dạng cấu trúc quá nhiều lần trong một cuộc đối thoại/bài viết, người ta có thể “rewrite” lại cấu trúc It take(s) bằng một cấu trúc tương đương sau:
| It take(s) + somebody + (time) + to + Verb = Somebody spend(s) + time + doing something. |
Ví dụ:
- It takes me 2 hours to finish this writing. (Mất 2 giờ đồng hồ để tôi hoàn thành bài viết này)
⇒ I spend 2 hours writing this. (Tôi dành 2 tiếng để viết bài này)
Bài tập ví dụ về cấu trúc It Take
Viết lại các câu sau đây dưới dạng cấu trúc It take(s)
- I walk to school in 20 minutes everyday.
- It takes Jess 30 minutes to remove her makeup everyday.
- She spends 20 minutes washing her dog every week.
- It takes me (30 minutes) to go to school. (Make question)
- We often spend 30 minutes reviewing our lesson before class.
Đáp án:
- It takes me 20 minutes to walk to school everyday.
- Jess spends 30 minutes removing her makeup everyday.
- It takes her 20 minutes to wash her dog every week.
- How long does it take you to go to school?
- It takes us 30 minutes to review our lesson before class.
Cấu trúc It Took và cách dùng
Cấu trúc It took chính là dạng quá khứ của It take(s). Hai cấu trúc này có cách sử dụng và cấu trúc tương tự nhau.
Cấu trúc It Took cơ bản
| It took + (time) + to + Verb |
| It took + somebody + (time) + to + Verb |
Ví dụ:
- It took Tuan almost 3 weeks to prepare for this performance. (Đã mất gần 3 tuần để Tuấn chuẩn bị cho phần trình diễn này)
Cấu trúc đặc biệt khác của It Took
| It took + (quantity + noun) to + Verb |
Ví dụ:
- It took Huong $1350 to get a round-trip flight ticket from HCM city to London this time last year! (Tốn tận 1350 đô-la để Hương mua một vé khứ hồi từ TP.HCM đến London vào thời điểm này năm ngoái đấy)
Cách viết lại câu với It Took
| It took + somebody + (time) + to + Verb = Somebody spent + time + doing something. |
Ví dụ:
- It took me 15 minutes to cook this dish. (Mất 15 phút để tôi nấu món này)
⇒ I spent 15 minutes cooking this dish. (Tôi tốn 15 phút để nấu món này)
Bài tập ví dụ về cấu trúc It Took
- He spent lots of time doing this experiment.
- Anna spent three days visiting VN.
- Last week, she spent 2 days tidying her room.
- They used to go to school in half an hour.
- Son Naeun spent 5 days visiting Danang.
Đáp án:
- It took him lots of time to do this experiment.
- It took Anna three days to visit VietNam.
- It took her two days to tidy her room.
- It took them half an hour to go to school.
- It took Son Naeun 5 days to visit Danang.
Cấu trúc spend và cách dùng

Đây là cấu trúc có cách sử dụng và ý nghĩa biểu đạt như cấu trúc It take(s)
Cấu trúc Spend đi cùng “V_ing”
| Subject + spend(s) + time/money + doing something |
Ví dụ:
- My aunt spends $6 buying this Starbucks coffee. (Dì tôi mua ly cà phê Starbucks này với giá 6 đô-la)
- I spend one and half hour everyday doing gym. (Tôi dành ra một tiếng ba mươi phút mỗi ngày để tập gym)
Cấu trúc Spend đi cùng Noun (Danh từ)
| Subject + spend(s) + time/money + on something = Subject + spend(s) + something |
Ví dụ:
- She spends all her money on this Gucci bag. (Cô ấy tiêu hết tiền của mình cho cái túi xách Gucci)
Viết lại câu với cấu trúc Spend
| It take(s) + somebody + (time) + to + Verb = Somebody spend(s) + time + doing something. |
Ví dụ:
- It has taken Trung 4 years to get that Administration Bachelor degree. (Mất tận 4 năm để Trung có thể gặt hái được cái bằng cử nhân Quản trị kinh doanh)
⇒ Trung has spent 4 years getting that Administration Bachelor degree. (Trung dành đến 4 năm để có được bằng cử nhân Quản trị kinh doanh)
Một số cấu trúc khác với spend
| Cấu trúc | Ví dụ |
| Subject + spend(s) + money + on doing something | My cousin has spent a lot of money on collecting stamps. (Em họ tôi tiêu hàng tá tiền cho bộ sưu tập tem) |
| Subject + spend(s) + time + in doing something | My deskmate spends almost of her freetime in playing violin. (Bạn cùng bàn của tôi dành phần lớn thời gian rảnh của cô ấy để chơi đàn vi-ô-lin) |
| Subject + spend(s) + something + on something | I tend to spend most of my effort on studying. (Tôi dường như dành hết mọi nỗ lực của mình cho việc học) |
| Spend itself = stop | Luckily, the Covid-19 pandemic spent itself after 3 years. (May mắn thay, đại dịch Covid-19 đã kết thúc sau 3 năm bùng nổ) |
Bài tập ví dụ về cấu trúc Spend
Câu 1: Điền Spend, waste, it takes vào chỗ trống phù hợp
- Why ______money on jewels you don’t need?
- He returned to his room, eager to _____ the day drawing.
- We won’t ______ our life being a monster!
- _______ time to gain weight just as________ time to lose it.
- His excellent cooking will _______ on those who do not appreciate it.
Đáp án:
- waste
- spend
- spend
- It takes – it takes
- be wasted
Câu 2: Hoàn thành các câu sau với cấu trúc Spend
- It’s not like me or my friends ever had any real money _____ at the mall.
- The average _____ per child is continuing to rise year-on-year.
- We _____ an average of 500 euro per year on new books.
- We _____ a lot of energy trying to be in fashion.
- On the weekends, wherever I got paid I _____ all my money in the bar.
Đáp án:
- It’s not like me or my friends ever had any real money to spend at the mall.
- The average spend per child is continuing to rise year-on-year.
- We had spent an average of 500 euro per year on new books.
- We spend a lot of energy trying to be in fashion.
- On the weekends, wherever I got paid I would spend all my money in the bar.
Bên trên là toàn bộ các nội dung liên quan đến cấu trúc spend và It takes. Hi vọng với các nội dung hữu ích và những bài tập cùng với lời giải chi tiết như trên sẽ hỗ trợ các bạn học sinh trong quá trình học tập.
Luận cứ là gì? Luận điểm là gì? Cách xác định và tìm luận điểm, luận cứ
Để tăng tính thuyết phục và độ mạch lạc cho một bài văn nghị luận, ta cần phải sử dụng đúng các luận điểm, luận cứ ở từng phần của bài văn. Vậy những luận điểm, luận cứ này là gì? Chúng giống hay khác nhau? Làm sao để xác định được đâu là luận điểm, còn đâu là luận cứ để đưa vào bài văn của mình? Bài viết của Bamboo School sau đây sẽ giải đáp các câu hỏi trên!
Luận cứ là gì?
Luận cứ chính là các dẫn chứng cụ thể được đưa ra nhằm làm cơ sở chứng minh các luận điểm được đề cập. Các luận cứ cần được xây dựng và tham khảo dựa trên các nguồn thông tin thực tế, số liệu khoa học hoặc các thực nghiệm thì mới có tính thuyết phục.
Các luận cứ cần phải đạt một số yêu cầu sau:
- Chân thật, đúng đắn
- Đã được xác thật (các định lý, định luật…)
- Phải mang tính logic, liên kết chặt chẽ với nhau
Luận cứ được chia thành 2 loại là lý thuyết và thực tiễn.
- Luận cứ lý thuyết: những luận cứ đã được giới khoa học chứng minh là đúng đắn (định lý, tiên đề, công thức, định luật, quy luật,…)
- Luận cứ thực tiễn: đây là những luận cứ được xác lập trên các cuộc thí nghiệm, thực nghiệm, phỏng vấn thực tế từ các công trình nghiên cứu khoa học có uy tín.

Luận điểm là gì?
Khi bạn đưa ra một quan điểm, một cách nhìn nhận bất kỳ về một vấn đề nào đó trong bài văn nghị luận, đó được xem là luận điểm. Một bài văn nghị luận được xây dựng dựa trên các luận điểm, từ những luận điểm này mà bạn sẽ phân tích và làm sáng tỏ quan điểm theo yêu cầu của bài viết.
Luận điểm của mỗi người là khác nhau và chúng không cần phải giống nhau hoàn toàn như một định lý, định luật (như là ở luận cứ).
Phân biệt luận điểm và luận cứ
| Luận điểm | Luận cứ | |
| Cơ sở xác lập | Ý tưởng; quan điểm của người viết | Thông tin xác thật đã được chứng minh trước đó |
| Chứng minh cho | Chứng minh cho quan điểm và lối tư duy, suy nghĩ của bản thân người viết | Luận điểm |
| Yêu cầu khác | Đúng đắn (có thể được chứng minh bởi các luận cứ) | Chính xác; logic; độ đáng tin cậy cao |
Cách xác định luận điểm, luận cứ trong bài văn nghị luận
Cách xác định luận điểm
Luận điểm được xác định trước khi ta viết một bài văn nghị luận. Luận điểm sẽ được xác định dựa trên cảm quan, cách nhìn nhận sự việc của người viết.
Sau đây là một số cách giúp bạn có thể xác định được luận điểm cho bài viết của mình;
- Theo dữ liệu được cung cấp sẵn tại đề bài.
- Dựa trên cách đặt câu hỏi.
- Dựa trên phương thức nghị luận.
Cách xác định luận cứ
Để có thể xác định những luận cứ chính xác nhằm chứng minh luận điểm của bản thân, đòi hỏi bạn cần có một vốn kiến thức nhất định vì những luận cứ này buộc phải chính xác, có tính khoa học và đã được chứng minh trước đó.
Trước hết hãy phân tích luận điểm mà bản thân đã đưa ra, từ đó xác định từng yếu tố một trong câu mà bạn cần phải chứng minh.
Ví dụ: “Thực hiện hoạt động PR, quảng bá sản phẩm qua các kênh social media rất quan trọng đối với một doanh nghiệp”
Khi này, bạn cần chứng minh vì sao lại phải quảng bá qua các kênh social media? Và vì sao hoạt động này lại quan trọng?
Chúng ta có một số luận cứ như sau:
- Xã hội hiện nay đang ở thời kỳ 4.0 (thời đại kỹ thuật số – cuộc cách mạng công nghệ)
- 2/3 dân số thế giới hiện đang sử dụng các trang mạng xã hội
- Quảng bá qua phương tiện social media giúp doanh nghiệp tiết kiệm chi phí hơn quảng cáo truyền thống mà lại tiếp cận được với nhiều khách hàng mục tiêu hơn.
Cách tìm luận điểm và luận cứ trong bài văn nghị luận
Tương tự như tại mục “Cách xác định luận điểm và luận cứ trong bài văn nghị luận”, để có thể tìm được luận điểm phù hợp với yêu cầu để bài. Trước hết bạn cần phải nắm và hiểu được yêu cầu chính của đề bài là gì? Từ đó dựa trên cách nhìn nhận và quan điểm cá nhân của chính mình để đưa ra các luận điểm phù hợp.
Cách tìm luận cứ sẽ có phần khó hơn đôi chút vì công việc này yêu cầu tính xác thật. Tuy nhiên nếu bạn không thể dẫn chứng được cụ thể số liệu chính xác thì có thể đưa ra những sự thật hiển nhiên để tăng phần thuyết phục cho bài viết của mình.
Ví dụ:
Thay vì phải nói rằng: “90% trường hợp mắc các bệnh ung thư phổi hiện nay được ghi nhận là do thuốc lá gây nên”
Ta có thể thay rằng: “Thuốc là chính là nguyên nhân chính dẫn đến các bệnh nguy hiểm về đường hô hấp, điển hình là ung thư phổi”
Bài tập ví dụ về luận điểm và luận cứ
Câu 1: Xác định các luận điểm, luận cứ của đoạn văn sau
“Tiếng Việt có những đặc sắc của một thứ tiếng đẹp, một thứ tiếng hay. Nói thế có nghĩa là nói rằng: tiếng Việt là một thứ tiếng hài hòa về mặt âm hưởng, thanh điệu mà cũng rất tế nhị, uyển chuyển trong cách đặt câu. Nói thế cũng có nghĩa là nói rằng: tiếng Việt có đầy đủ khả năng để diễn đạt tình cảm, tư tưởng của người Việt Nam và để thỏa mãn cho nhu cầu đời sống văn hóa nước nhà qua các thời kỳ lịch sử” (Đặng Thai Mai – Sự giàu đẹp của tiếng Việt)
Hướng dẫn:
Luận điểm:
- Tiếng Việt có những đặc sắc riêng của một thứ tiếng đẹp, một thứ tiếng hay.
Các luận cứ gồm:
- Tiếng Việt là một thứ tiếng hài hòa về mặt âm hưởng, thanh điệu mà cũng rất tế nhị, uyển chuyển trong cách đặt câu.
- Tiếng Việt có đầy đủ khả năng để diễn đạt tình cảm, tư tưởng của người Việt Nam và để thỏa mãn cho nhu cầu đời sống văn hóa nước nhà qua các thời kỳ lịch sử
Câu 2: Đoạn văn sau đây đang trình bày về luận điểm nào?
Quan lại vì tiền mà bất chấp công lý; sai nha vì tiền mà tra tấn cha con Vương Ông; Tú Bà; Mã Giám Sinh, Bạc Bà, Bạc Hạnh vì tiền mà làm nghề buôn bán thịt người; Sở Khanh vì tiền mà táng tận lương tâm; Khuyển Ưng vì tiền mà lao vào tội ác. Cả một xã hội chạy theo tiền. (Hoài Thanh)
- Xã hội trong Truyện Kiều là một xã hội vô nhân đạo
- Xã hội trong Truyện Kiều là một xã hội bất công.
- Xã hội trong Truyện Kiều là một xã hội chạy theo đồng tiền.
- Xã hội trong Truyện Kiều là một xã hội vùi dập nhân tài.
Xem thêm:
- Đặc điểm, phân biệt và cách xác định 6 phong cách ngôn ngữ chi tiết đầy đủ nhất
- Nói giảm nói tránh là gì? Tác dụng, ví dụ và cách nói giảm nói tránh
- Từ đồng âm là gì? Phân loại, cách nhận biết và bài tập về từ đồng âm
Các bạn vừa xem qua bài viết nói về luận điểm và luận cứ. Bài viết với mong muốn hỗ trợ các bạn học sinh trong việc xây dựng một hệ thống các dẫn chứng và lập luận thuyết phục cho các bài văn của mình. Mong rằng các bạn sẽ tìm được thông tin có ích cho mình thông qua bài viết này nhé!
Vận tốc là gì? Đơn vị, kí hiệu và cách tính vận tốc
Vận tốc là một đại lượng được nhắc đến phổ biến trong kiến thức Vật lý cũng như trong đời sống thực tiễn. Vậy vận tốc là gì và được kí hiệu như thế nào? Công thức tính vận tốc cơ bản và nâng cao? Hãy để bài viết dưới đây giúp bạn nắm rõ hơn những kiến thức căn bản và các dạng bài tập tính vận tốc trong các kỳ thi. Cùng Bamboo School chúng mình tìm hiểu ngay nhé!
Vận tốc là gì?
Trong Vật lý, vận tốc chính là quãng đường mà một vật đi được trong một đơn vị thời gian nhất định. Thông qua vận tốc, chúng ta có thể xác định được tốc độ di chuyển nhanh hay chậm của chuyển động, nhờ vào việc tính độ dài của quãng đường đi được trong một khoảng thời gian bất kỳ.

Vận tốc là quãng đường một vật di chuyển được trong một đơn vị thời gian
Đơn vị và kí hiệu vận tốc
Vận tốc được quy ước kí hiệu bằng chữ v. Đơn vị đo của vận tốc khá đa dạng, vì nó tùy thuộc vào đơn vị đo độ dài và thời gian. Tuy nhiên, đa số các trường hợp, người ta thường sử dụng các đơn vị sau đây để đo vận tốc: km/h, m/s.
Trong đó:
- 1 m/s = 18/5 km/h = 3,6 km/h
- 1 km/h = 5/18 m/s = 0.277777778 m/s

Vận tốc được kí hiệu bằng chữ v và có đơn vị là m/s hoặc km/h
Công thức tính vận tốc
Công thức tính vận tốc bất kỳ được quy định như sau:
v = S/t
Trong đó:
- v là vận tốc của một vật, đơn vị là km/h hoặc m/s
- S là quãng đường vật di chuyển, đơn vị là km hoặc m
- t là thời gian mà vật đi hết quãng đường đó, đơn vị là h hoặc s (giờ hoặc giây)

Công thức tính vận tốc là v = S/t
Các công thức tính vận tốc nâng cao
Từ công thức tính vận tốc đã nêu ở trên, tùy theo từng trường hợp, từng dạng đề cụ thể mà ta sẽ áp dụng các công thức tính vận tốc nâng cao để cho ra kết quả chính xác nhất.
Cách tính vận tốc tương đối
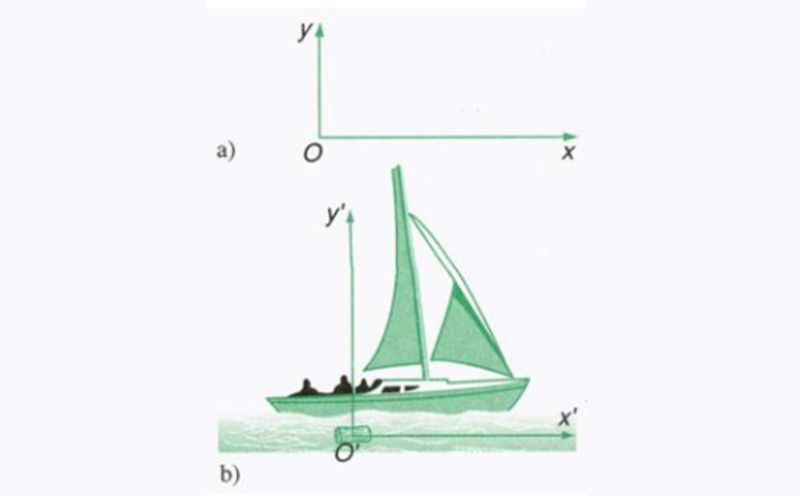
Để tính vận tốc tương đối, ta sẽ xem xét chuyển động của vật trong hai hệ quy chiếu khác nhau. Ở đây, ta sẽ ví dụ bằng hình ảnh một chiếc thuyền chạy trên sông.
Gọi xOy là hệ quy chiếu khi vật đứng yên. x’O’y’ là hệ quy chiếu khi vật chuyển động.
Lúc này, thuyền được kí hiệu là số 1 (tương ứng với một vật đang chuyển động), nước được kí hiệu là số 2 (tương ứng với hệ quy chiếu chuyển động), bờ được kí hiệu là số 3 (tương ứng với hệ quy chiếu đứng yên).
v1,3 là vận tốc của thuyền đối với bờ, còn được gọi là vận tốc tuyệt đối. v1,2 là vận tốc của thuyền đối với nước, được gọi là vận tốc tương đối. v2,3 là vận tốc của nước đối với bờ, được gọi là vận tốc kéo theo.
Ta có công thức sau đây: v1,3→ = v1,2→ + v2,3→
Để tính vận tốc tương đối của một vật, ta xét vật đó trong hệ quy chiếu khi vật đứng yên và hệ quy chiếu khi vật chuyển động
Cách tính vận tốc dòng nước
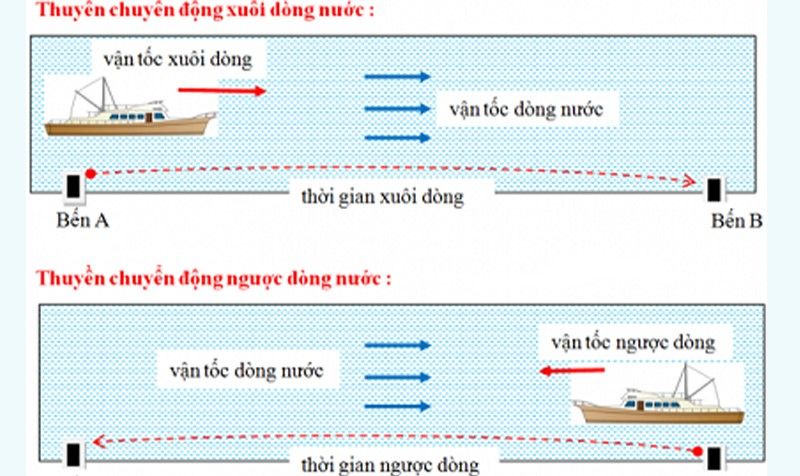
Công thức tính vận tốc dòng nước được áp dụng theo các trường hợp cụ thể dưới đây:
- Nếu vật chuyển động xuôi theo dòng nước thì: Vận tốc xuôi dòng = vận tốc của vật + vận tốc dòng nước
- Nếu vật chuyển động ngược dòng thì: Vận tốc ngược dòng = vận tốc của vật – vận tốc dòng nước
- Vận tốc dòng nước = (vận tốc xuôi dòng – vận tốc ngược dòng)/2
Vận tốc dòng nước = (vận tốc xuôi dòng – vận tốc ngược dòng)/2
Cách tính vận tốc tức thời
Công thức tính vận tốc tức thời được quy ước như sau:
vtt = dr/dt
Trong đó:
- vtt là vận tốc tức thời của vật
- r là quãng đường vật di chuyển được trong một đơn vị thời gian
- t là thời gian vật đi được quãng đường bất kỳ
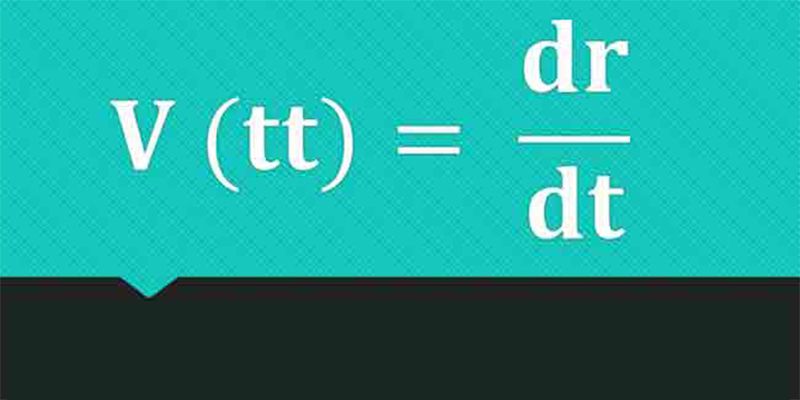
Vận tốc tức thời vtt = dr/dt
Cách tính vận tốc quãng đường thời gian
Từ công thức tính vận tốc ban đầu, ta có thể suy ra được công thức tính quãng đường và thời gian mà vật di chuyển hết quãng đường đó:
S = v.t
t = S/v
(Đơn vị đo của v là m/s hoặc km/h, của S là m hoặc km, của t là s hoặc h).
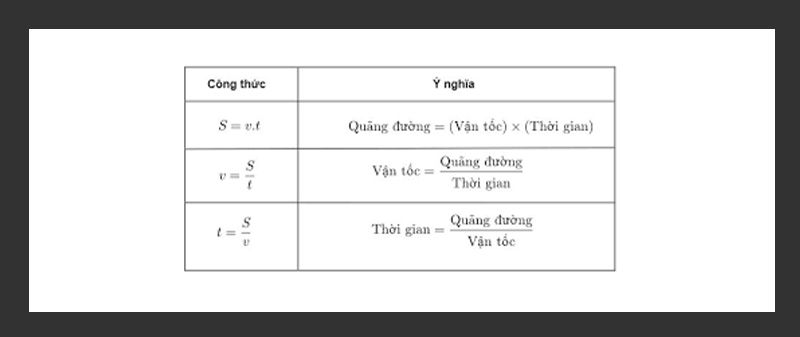
Bảng tính vận tốc, quãng đường, thời gian di chuyển của một vật bất kỳ
Cách tính vận tốc trung bình
Vận tốc trung bình được tính bằng công thức dưới đây:
vtb = S/Δt
Trong đó:
- vtb là vận tốc trung bình của vật
- S là tổng quãng đường mà vật di chuyển được
- Δt là thời gian chuyển động của vật. Δt = t2 – t1

Công thức tính vận tốc trung bình của một vật
Bài tập vận dụng có đáp án
Dưới đây là một số dạng bài tập vận dụng về vận tốc kèm đáp án, lời giải chi tiết. Mời các bạn cùng tham khảo.
Bài tập 1: Trong các phát biểu dưới đây, phát biểu nào là sai?
A. Vận tốc được tính bằng công thức v = S/t
B. Vận tốc là quãng đường đi được trong một đơn vị thời gian
C. Đơn vị của vận tốc là s
D. Đơn vị của vận tốc là m/s
Đáp án: C
Bài tập 2: 1 m/s bằng bao nhiêu km/h?
A. 3,6 km/h
B. 36 km/h
C. 7,2 km/h
D. 72 km/h
Đáp án: A
Bài tập 3: Độ lớn của vận tốc có thể cung cấp cho ta thông tin gì về chuyển động của vật?
A. Cho biết hướng chuyển động của vật.
B. Cho biết vật chuyển động theo quỹ đạo nào.
C. Cho biết vật chuyển động nhanh hay chậm.
D. Cho biết nguyên nhân vì sao vật lại chuyển động được.
Đáp án: C
Bài tập 4: Lúc 8 giờ, một người đi xe đạp khởi hành từ A về B với vận tốc 5 m/s. Lúc 10 giờ một người đi xe máy từ A về B với vận tốc 36 km/h. Hai người này gặp nhau lúc mấy giờ? Nơi gặp nhau cách A bao nhiêu km?
Đáp án:
Gọi t là thời gian của người đi xe đạp kể từ khi xuất phát cho đến khi gặp nhau.
Gọi thời gian của người đi xe máy kể từ khi xuất phát cho đến khi gặp nhau là t -1.
Quãng đường đi được của người đi xe đạp là:
sĐ = vĐ.t = 5.3,6.t = 18t (1)
Quãng đường đi được của người đi xe máy là:
sM = vM.t = 36.(t – 1) = 36t – 36 (2)
Khi hai người gặp nhau thì sĐ = sM (3)
Từ (1), (2), (3) suy ra: 18t = 36t – 36 => t = 2 giờ
Vậy sau khoảng thời gian 9 + 2 = 11 giờ thì hai người gặp nhau.
Nơi gặp nhau cách A số km là: sĐ = 18.2 = 36 (km).
Bài tập 5: Một người đi xe máy xuất phát tại A vào lúc 7 giờ 20 phút và đến B lúc 8 giờ 5 phút. Quãng đường từ A đến B là 24,3 km. Tính vận tốc của người đó theo km/h và m/s.
Đáp án:
Thời gian người đi xe máy đi từ A đến B là:
t = 8 giờ 5 phút – 7 giờ 20 phút = 45 phút = 2700 giây
Quãng đường từ A đến B là 24,3 km = 24300 m
Vận tốc của người đi xe máy là:
v = S/t = 24300/2700 = 9 (m/s) = 32,4 km/h
Bài tập 6: Trong đêm tối, từ lúc nhìn thấy tia chớp lóe sáng cho đến khi nghe thấy tiếng bom nổ khoảng 15 giây. Vận tốc truyền âm trong không khí là 340 m/s. Hỏi khoảng cách giữa chỗ bom nổ và người quan sát là bao nhiêu?
Đáp án:
Khoảng cách giữa chỗ bom nổ và người quan sát là:
S = v.t = 340.15 = 5100 (m)
Bài tập 7: Trên cùng một quãng đường dài 21 km, ô tô đi hết 24 phút còn xe máy đi hết 36 phút. Vận tốc của xe nào lớn hơn và lớn hơn bao nhiêu km?
Đáp án:
24 phút = 0,4 giờ. 36 phút = 0,6 giờ
Vận tốc của ô tô là:
v = S/t = 21/0,4 = 52,5 (km/h)
Vận tốc của xe máy là:
v = S/t = 21/0,6 = 35 (km/h)
Vì 52,5 km/h > 35 km/h nên vận tốc của ô tô lớn hơn xe máy.
Hiệu hai vận tốc là:
52,5 – 35 = 17,5 (km/h)
Bài tập 8: Quãng đường AB gồm một đoạn lên dốc dài 15,3 km và một đoạn xuống dốc dài 24 km. Một ô tô đi lên dốc hết 54 phút và đi xuống dốc hết 36 phút. Tính:
a) Vận tốc của ôt ô khi lên dốc và xuống dốc.
b) Vận tốc trung bình của ô tô trên cả quãng đường AB.
Đáp án:
54 phút = 0,9 giờ. 36 phút = 0,6 giờ
a) Vận tốc của ô tô khi lên dốc là:
v = S/t = 15,3/0,9 = 17 (km/h)
Vận tốc của ô tô khi xuống dốc là:
v = S/t = 24/0,6 = 40 (km/h)
b) Thời gian ô tô đi quãng đường AB là:
t = 0,9 + 0,6 = 1,5 (h)
Độ dài quãng đường AB là:
S = 15,3 + 24 = 39,3 (km)
Vận tốc trung bình của ô tô trên cả quãng đường AB là:
v = S/t = 39,3/1,5 = 26,2 (km/h)
Xem thêm:
- Cách Tính Mét Vuông (m2) Chính Xác, Đơn Giản Nhất
- Điện trở là gì? Tính chất và công thức tính điện trở đầy đủ và chi tiết
- Áp suất là gì? Đơn vị và công thức tính áp suất
Hy vọng bài viết trên đã giúp bạn nắm được các công thức tính vận tốc, cũng như biết cách áp dụng công thức vào nhiều dạng bài tập khác nhau. Chúc các bạn gặt hái được kết quả cao trong những kỳ thi sắp tới!
Đặc điểm, phân biệt và cách xác định 6 phong cách ngôn ngữ chi tiết đầy đủ nhất
Trong ngôn ngữ nói và viết hằng ngày, ta có thể bắt gặp nhiều kiểu phong cách ngôn ngữ khác nhau. Trong đó, phong cách ngôn ngữ sinh hoạt là một trong những phong cách ngôn ngữ phổ biến nhất. Vậy nó có đặc điểm như thế nào? Làm sao để nhận biết phong cách ngôn ngữ sinh hoạt với những kiểu phong cách ngôn ngữ còn lại? Hãy cùng Bamboo School chúng mình giải đáp những thắc mắc này qua bài viết dưới đây nhé!
Phong cách ngôn ngữ là gì?
Trước khi tìm hiểu phong cách ngôn ngữ sinh hoạt, ta cần hiểu được phong cách ngôn ngữ là gì. Phong cách có thể hiểu một cách đơn giản là những đặc điểm riêng, nét đặc trưng, điểm nhấn để ta phân biệt sự vật, sự việc, hiện tượng này,… với những sự vật, hay sự việc, hiện tượng… khác.
Tương tự, phong cách ngôn ngữ chính là những nét riêng, nét đặc trưng của từng kiểu diễn đạt ngôn ngữ (cả về nói và viết) trong đời sống hằng ngày. Từ đó, ta có thể phân biệt được phong cách ngôn ngữ này với phong cách ngôn ngữ khác, và biết cách áp dụng đúng những phong cách ngôn ngữ phù hợp vào những ngữ cảnh cụ thể trong giao tiếp.

Phong cách ngôn ngữ là những nét riêng, nét đặc trưng của từng kiểu diễn đạt ngôn ngữ (cả về nói và viết)
Các phong cách ngôn ngữ
Trong tiếng Việt, phong cách ngôn ngữ được chia thành 6 loại, mỗi loại đều có những đặc điểm riêng. Đó là:
- Phong cách ngôn ngữ sinh hoạt
- Phong cách ngôn ngữ khoa học
- Phong cách ngôn ngữ nghệ thuật
- Phong cách ngôn ngữ báo chí
- Phong cách ngôn ngữ hành chính
- Phong cách ngôn ngữ chính luận
Phong cách ngôn ngữ sinh hoạt
Phong cách ngôn ngữ đầu tiên, và cũng được xem là kiểu cơ bản nhất chính là phong cách ngôn ngữ sinh hoạt.
- Đặc điểm: Phong cách ngôn ngữ sinh hoạt sử dụng lời ăn tiếng nói hằng ngày như thư từ, nhật ký, tin nhắn, trò chuyện,… và được sử dụng trong các đoạn hội thoại, giao tiếp trong đời sống. Kiểu phong cách ngôn ngữ này thể hiện được tính cá thể (thường là những cá nhân giao tiếp với nhau), tính cảm xúc (biểu thị rõ thái độ, tình cảm, tâm tư,… của người nói hoặc người viết) và tính cụ thể về nội dung giao tiếp, bối cảnh giao tiếp,…
- Cách nhận biết: Cách nhận biết phong cách ngôn ngữ sinh hoạt rất đơn giản. Ta dựa vào từ ngữ, ngữ pháp được người nói (hay người viết) sử dụng. Ngôn ngữ sinh hoạt mang tính chất bình dân, đơn giản và dễ hiểu, không sử dụng các thuật ngữ liên quan đến học thuật.

Phong cách ngôn ngữ sinh hoạt sử dụng lời ăn tiếng nói hằng ngày
Phong cách ngôn ngữ Khoa học
Phong cách ngôn ngữ khoa học có những đặc điểm và cách nhận biết như sau:
- Đặc điểm: Đúng như tên gọi, đây là kiểu phong cách ngôn ngữ thường được sử dụng trong phạm vi thuộc về các lĩnh vực khoa học nào đó. Phong cách ngôn ngữ khoa học thể hiện tính khái quát và trừu tượng, tính lí trí, logic và tính khách quan, phi cá thể.
- Cách nhận biết: Để nhận biết phong cách ngôn ngữ khoa học trong các văn bản, ta cần xem xét các từ ngữ, khái niệm, định nghĩa,… mang tính chuyên môn về một khía cạnh, vấn đề, hoặc một lĩnh vực nào đó trong cuộc sống.
Phong cách ngôn ngữ Khoa học được sử dụng trong phạm vi thuộc về các lĩnh vực khoa học nào đó
Phong cách ngôn ngữ nghệ thuật
Về đặc điểm và cách nhận biết, phong cách ngôn ngữ sinh hoạt có những điểm cần lưu ý sau đây:
- Đặc điểm: Phong cách ngôn ngữ nghệ thuật chủ yếu được sử dụng trong những tác phẩm nghệ thuật ở cả dạng nói và dạng viết. Đó có thể là truyện ngắn, tiểu thuyết, thơ ca, âm nhạc, chèo, tuồng, kịch,… Ngôn ngữ thuộc kiểu phong cách này được trau chuốt cẩn thận hơn ngôn ngữ thông thường, sao cho mang đến giá trị thẩm mỹ cao. Bên cạnh đó, phong cách ngôn ngữ nghệ thuật còn đề cao tính cá thể, tính cảm xúc và thường sử dụng các phép tu từ, biện pháp nghệ thuật (như so sánh, nhân hóa, ẩn dụ, chơi chữ,…).
- Cách nhận biết: Để phân biệt phong cách ngôn ngữ nghệ thuật với các kiểu phong cách ngôn ngữ còn lại, ta sẽ xét đến ngữ cảnh giao tiếp, tính truyền cảm và cách trau chuốt từ ngữ của người nói hoặc người viết, các biện pháp nghệ thuật được sử dụng,…

Phong cách ngôn ngữ nghệ thuật được sử dụng trong văn xuôi, thơ ca, âm nhạc,…
Phong cách ngôn ngữ báo chí
Tương tự với các kiểu phong cách ngôn ngữ sinh hoạt, khoa học và nghệ thuật, phong cách ngôn ngữ báo chí cũng được sử dụng rất phổ biến trong đời sống hằng ngày.
- Đặc điểm: Phong cách ngôn ngữ báo chí được sử dụng ở cả dạng nói và dạng viết, như: Tin, bài, phóng sự, phát thanh, truyền hình,… Mục đích khi sử dụng phong cách ngôn ngữ báo chí là để người làm báo, cơ quan báo chí,… phản ánh một cách khách quan và trung thực về các vấn đề, sự việc, hiện tượng,… nóng hổi xảy ra trong đời sống, được dư luận xã hội đặc biệt quan tâm, nhằm đáp ứng nhu cầu thông tin của công chúng. Phong cách ngôn ngữ báo chí đề cao tính thời sự, tính ngắn gọn, xúc tích về dễ hiểu đối với mọi đối tượng công chúng.
- Cách nhận biết: Để nhận biết phong cách ngôn ngữ báo chí trong các văn bản ở dạng nói và viết, ta sẽ dựa vào cách lập luận và sử dụng từ ngữ. Lập luận trong văn bản báo chí thường ngắn gọn, súc tích và rõ ràng, đưa ra các số liệu, dẫn chứng chặt chẽ để thuyết phục được người đọc hoặc người xem. Bên cạnh đó, từ ngữ được sử dụng phải là các từ ngữ bình dân, dễ hiểu và dễ tiếp cận với mọi đối tượng công chúng. Nếu đưa ra các thuật ngữ chuyên môn thì phải giải thích rõ thuật ngữ đó.

Phong cách ngôn ngữ báo chí được sử dụng ở cả dạng nói và viết
Phong cách ngôn ngữ Hành chính
Phong cách ngôn ngữ hành chính là kiểu phong cách ngôn ngữ chỉ được sử dụng trong các loại văn bản hành chính – công vụ, và ít phổ biến hơn phong cách ngôn ngữ sinh hoạt.
- Đặc điểm: Phong cách ngôn ngữ hành chính thường được trình bày theo những khuôn mẫu đã có sẵn, người viết (hay người nói) phải tuân thủ chặt chẽ. Ngoài ra, trong các văn bản hành chính, người viết thường sử dụng các câu văn dài, tách những ý quan trọng thành nhiều đoạn nhỏ. Phong cách ngôn ngữ hành chính thể hiện rõ tính công vụ (không đề cập đến tính cá thể, thường mang ý nghĩa toàn dân), không sử dụng các từ ngữ địa phương mà chỉ dùng từ ngữ mang tính ước lệ, không sử dụng các phép tu từ nghệ thuật, chỉ sử dụng lối diễn đạt dễ hiểu và ngắn gọn, tuân theo các khuôn mẫu nhất định.
- Cách nhận biết: Ta có thể dựa vào các từ ngữ mang tính ước lệ, công vụ để nhận biết phong cách ngôn ngữ hành chính với các kiểu phong cách ngôn ngữ còn lại. Ví dụ như các từ: kính gửi, kính mong, trân trọng,… hay bố cục của một văn bản (có quốc hiệu và tiêu ngữ, người nhận hay cơ quan tiếp nhận văn bản, các chương – điều – khoản, tên và chữ ký của người gửi…).

Phong cách ngôn ngữ Hành chính được trình bày theo những khuôn mẫu đã có sẵn
Phong cách ngôn ngữ Chính luận
Về đặc điểm và cách nhận biết phong cách ngôn ngữ chính luận, ta sẽ dựa vào những điểm dưới đây:
- Đặc điểm: Phong cách ngôn ngữ chính luận chủ yếu được dùng trong các loại văn bản chính luận, hay trong các cuộc họp, hội nghị, hội thảo,… Đặc trưng của kiểu phong cách ngôn ngữ này là đề cập, đánh giá, bình luận, thảo luận,… về một vấn đề, khía cạnh, lĩnh vực nào đó trong đời sống xã hội. Trong phong cách ngôn ngữ chính luận, ta có thể sử dụng biện pháp tu từ để tăng tính chặt chẽ, thuyết phục và logic cho lập luận, luận điểm của mình. Đồng thời, các từ ngữ được dùng phải đảm bảo tính tuyền cảm và thuyết phục, sử dụng một hệ thống luận cứ, dẫn chứng rõ ràng và đầy đủ.
- Cách nhận biết: Thông thường, trong các văn bản chính luận, người viết hay người nói thường sử dụng nhiều từ ngữ chính trị, xây dựng lối diễn đạt, lập luận súc tích, có tính liên kết chặt chẽ với nhau. Ngoài ra, các từ ngữ trong văn bản chính luận phải cụ thể và rõ ràng, tránh mơ hồ về nghĩa, sử dụng các luận điểm, dẫn chứng cụ thể và xác đáng. Ta có thể dựa vào những điểm này để nhận biết kiểu phong cách ngôn ngữ chính luận.

Đặc điểm của phong cách ngôn ngữ Chính luận là đánh giá, bình luận, thảo luận,… về một vấn đề, khía cạnh, lĩnh vực nào đó
Bảng phân biệt so sánh các loại phong cách ngôn ngữ
Dưới đây là bảng phân biệt so sánh về đặc điểm, tính chất của 6 loại phong cách ngôn ngữ thông dụng nhất. Mời các bạn cùng tham khảo.
|
STT |
Kiểu phong cách ngôn ngữ | Đặc điểm |
Tính chất |
|
1 |
Phong cách ngôn ngữ sinh hoạt | Chủ yếu được sử dụng trong giao tiếp, sinh hoạt hàng ngày. Ví dụ như thư từ, nhật ký, tin nhắn, đối thoại trò chuyện,… |
|
|
2 |
Phong cách ngôn ngữ khoa học | Được dùng trong các văn bản khoa học. Ví dụ như: Nghiên cứu khoa học, bài giảng, giáo án, giáo trình, tài liệu chuyên sâu, sách giáo khoa,… |
|
|
3 |
Phong cách ngôn ngữ nghệ thuật | Được sử dụng trong các tác phẩm nghệ thuật ở dạng nói và dạng viết. Có thể kể đến như: Văn xuôi, thơ ca, kịch, hát chèo,… |
|
|
4 |
Phong cách ngôn ngữ báo chí | Được sử dụng trong các văn bản báo chí ở dạng nói và viết. Ví dụ: Tin tức báo chí, phóng sự, bài báo, phát thanh – truyền hình,… |
|
|
5 |
Phong cách ngôn ngữ hành chính | Chủ yếu được sử dụng trong các loại văn bản hành chính. Có thể kể đến như: Công văn, tờ trình, biên bản, thông báo, quyết định, luật,… |
|
|
6 |
Phong cách ngôn ngữ chính luận | Chủ yếu được sử dụng trong các văn bản chính luận, hoặc trong các buổi hội thảo, hội nghị, các cuộc họp,… |
|

Phân biệt 6 loại phong cách ngôn ngữ trong tiếng Việt
Bài tập và ví dụ về các phong cách ngôn ngữ
- Bài tập 1: Nhận định nào dưới đây là sai?
A. Phong cách ngôn ngữ sinh hoạt có thể được dùng trong các văn bản hành chính
B. Trong phong cách ngôn ngữ chính luận, ta phải xây dựng hệ thống luận điểm, dẫn chứng chặt chẽ và rõ ràng
C. Phong cách ngôn ngữ nghệ thuật được dùng trong các tác phẩm tiểu thuyết, thơ, truyện ngắn,…
D. Phong cách ngôn ngữ khoa học được sử dụng trong các giáo trình, tài liệu khoa học,…
Đáp án: A
- Bài tập 2: Văn bản nào dưới đây sử dụng phong cách ngôn ngữ hành chính?
A. Bài báo
B. Công văn
C. Sách, vở
D. Nhật ký
Đáp án: B
- Bài tập 3: Chỉ ra phong cách ngôn ngữ có trong đoạn trích dưới đây?
“Cuộc đời ai cũng có những tấm lòng
Để làm giấy chứng minh
Để cầu mong thành đạt
Những tấm bằng như những bảng chỉ đường qua những đường phố hẹp
Để đến đại lộ cuộc đời ngày càng mở rộng thêm…”
(Trích Tấm bằng – Hoàng Ngọc Quý)
Đáp án: Đoạn trích trên sử dụng phong cách ngôn ngữ nghệ thuật.
- Bài tập 4: Tìm các thuật ngữ khoa học có trong đoạn trích dưới đây:
“Ngôn ngữ là yếu tố thứ nhất của văn học, là chất liệu của văn chương, văn học là nghệ thuật ngôn ngữ. Những điều đó đã được thừa nhận một cách hiển nhiên, dường như không có gì phải bàn cãi. Từ đó, nghiên cứu văn học nhất thiết không thể bỏ qua bình diện ngôn ngữ văn học, không chỉ bởi vì mọi yếu tố, mọi bình diện khác của văn học đều chỉ có thể được biểu đạt qua ngôn ngữ, mà còn vì sáng tạo ngôn ngữ là một trong những mục đích quan trọng, cũng là một phần không nhỏ trong sự đóng góp vào những giá trị độc đáo, riêng biệt của văn chương. Lịch sử văn học, xét về một phương diện cũng chính là lịch sử của ngôn ngữ văn học.
Ngôn ngữ văn học vừa là điều kiện, lại vừa là kết quả của quá trình vận động, biến đổi của văn học qua các thời kỳ, giai đoạn. Sự thay đổi hệ hình văn học cũng đi liền với sự thay đổi của hệ hình ngôn ngữ văn học, và qua đó phản ánh sự biến đổi của đời sống xã hội, của tư duy, của môi trường văn hóa tinh thần và các giá trị của quan niệm thẩm mỹ”.
Đáp án: Các thuật ngữ khoa học có trong đoạn trích trên: Ngôn ngữ, chất liệu của văn chương, nghệ thuật ngôn ngữ, bình diện ngôn ngữ, văn chương, quan niệm thẩm mỹ, hệ hình văn học.
- Bài tập 5: Viết một đoạn văn sử dụng phong cách ngôn ngữ khoa học, có đề tài về môi trường.
Đáp án (tham khảo): Môi trường là nơi mà các sinh vật cùng sinh sống. Tuy nhiên hiện nay, môi trường sống của con người đang bị hủy hoại nghiêm trọng. Điều này xuất phát từ việc ô nhiễm nguồn nước, không khí, ô nhiễm đất,… Bên cạnh đó, hiện tượng nóng lên toàn cầu đã dẫn đến băng tan ở hai cực, ảnh hưởng xấu đến môi trường sống của các loài sinh vật. Những hình thức thời tiết cực đoan như mưa đá, sương muối, băng tuyết diễn ra ngày càng nhiều hơn, đe dọa đến cuộc sống của con người. Chính vì vậy, con người cần phải nâng cao hơn nữa ý thức bảo vệ môi trường để bảo vệ cuộc sống của chính mình.
Xem thêm:
- Điệp từ là gì? Điệp ngữ là gì? Cấu trúc và ví dụ minh họa
- Từ đồng âm là gì? Phân loại, cách nhận biết và bài tập về từ đồng âm
- Từ khởi ngữ là gì? Tác dụng, dấu hiệu nhận biết và ví dụ minh họa về từ khởi ngữ
Trên đây là 6 loại phong cách ngôn ngữ thông dụng nhất trong tiếng Việt và một số bài tập vận dụng mà bạn có thể tham khảo. Hy vọng bài viết trên đã mang đến cho bạn nhiều kiến thức bổ ích. Chúc bạn luôn đạt được kết quả cao trong môn Ngữ văn.
Định luật ôm là gì? Kí hiệu, ý nghĩa, công thức và bài tập vận dụng về định luật ôm
Bạn thường nghe về định luật ôm trong môn vật lý ở trường, nhưng bạn đã nắm rõ về khái niệm, kí hiệu, ý nghĩa và công thức của định luật ôm là gì hay chưa? Nếu chưa, thì những thông tin dưới đây là dành cho bạn, nhằm giúp bạn hiểu rõ về lý thuyết, cũng như có thể vận dụng để làm bài tập về định luật ôm một cách nhanh chóng.
Khái niệm định luật Ôm
Định luật ôm là cường độ dòng điện chạy qua dây dẫn tỷ lệ thuận với hiệu điện thế đặt vào hai đầu dây dẫn và tỷ lệ nghịch với điện trở của dây dẫn.
Ngoài ra, định luật ôm còn phụ thuộc vào cường độ dòng điện của hiệu điện thế và điện trở. Nội dung của định luật cho rằng cường độ dòng điện đi qua hai điểm của một vật dẫn điện luôn tỷ lệ thuận với hiệu điện thế đi qua hai điểm đó, với vật dẫn điện có điện trở là một hằng số.
Định luật ôm cho toàn mạch là cường độ dòng điện chạy trong mạch kín sẽ tỷ lệ thuận với suất điện động của nguồn điện và tỷ lệ nghịch với điện trở toàn phần của mạch đó.

Khái niệm về định luật ôm
Đơn vị, kí hiệu định luật ôm
Ngoài việc tìm hiểu về khái niệm của định luật ôm thì đơn vị, kí hiệu cũng rất quan trọng nhằm giúp các bạn có thể nhận dạng một cách dễ dàng thông qua đơn vị và kí hiệu của nó:
Ôm là đơn vị đo của điện trở và kí hiệu của ôm là Ω. Ngoài ra, cách để quy đổi ra ôm là:
- 1 Kilôôm = 1 kΩ = 1000 Ω
- 1 Mega Ôm = 1 MΩ = 1000000 Ω
Ý nghĩa định luật ôm
Định luật ôm dùng để mô tả cho mối quan hệ giữa ba đại lượng là cường độ dòng điện, hiệu điện thế và điện trở. Nhằm mục đích giúp chúng ta có thể đo lường chính xác các giá trị tĩnh của những linh kiện có trong mạch, nguồn cung cấp của điện áp hay giảm điện áp và cường độ của dòng điện mà các vật dụng đo lường như ampe kìm, đồng hồ vạn năng,…không cho ra các giá trị chính xác được.

Ý nghĩa của định luật ôm
Công thức định luật ôm
Định luật ôm có công thức là: I = U/R
Trong đó:
- I (đơn vị: ampe, ký hiệu: A) là cường độ dòng điện đi qua vật dẫn
- U (đơn vị: vôn, ký hiệu: V) là điện áp trên vật dẫn
- R (đơn vị: ôm, ký hiệu: Ω) là điện trở
Lưu ý:
- Cường độ dòng điện phụ thuộc vào hiệu điện thế và điện trở
- Hiệu điện thế không phụ thuộc vào điện trở và cường độ dòng điện
- Điện trở không phụ thuộc vào hiệu điện thế và cường độ dòng điện
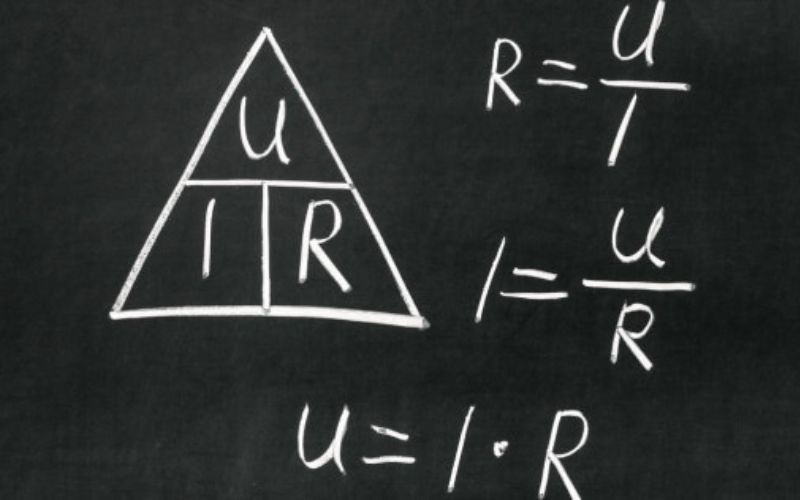
Công thức để tính định luật ôm
Bài tập ví dụ vận dụng về định luật ôm – Có đáp án
Từ những lý thuyết về khái niệm, ý nghĩa, công thức của định luật ôm thì dưới đây là một số bài tập ví dụ nhằm giúp các bạn có thể vận dụng và hiểu rõ hơn về định luật ôm, để có thể dễ dàng làm các bài tập liên quan đến định luật ôm trên lớp học và trong các bài kiểm tra.

Bài tập về định luật ôm
Bài tập 1: Nếu tăng hiệu điện thế giữa hai đầu một dây dẫn lên 3 lần thì cường độ dòng điện chạy qua dây dẫn này thay đổi như thế nào?
A. Giảm 3 lần
B. Tăng 3 lần
C. Không thay đổi
D. Tăng 1,5 lần
Hướng dẫn cách giải:
Nếu tăng hiệu điện thế giữa hai đầu của một dây dẫn lên 3 lần thì cường độ dòng điện cũng tăng lên 3 lần. Vì cường độ dòng điện chạy qua dây dẫn sẽ tỷ lệ thuận với hiệu điện thế đặt vào hai đầu đoạn mạch, nên hiệu điện thế tăng lên bao nhiêu lần thì cường độ dòng điện cũng tăng lên bấy nhiêu lần.
Vậy nên chúng ta sẽ chọn đáp án B
Bài tập 2: Khi đặt vào hai đầu dây dẫn một hiệu điện thế 12V thì cường độ dòng điện chạy qua nó là 0,5A. Nếu hiệu điện thế đặt vào hai đầu dây dẫn đó tăng lên đến 36V thì cường độ dòng điện chạy qua nó là bao nhiêu?
Hướng dẫn cách giải:
Cường độ dòng điện chạy qua dây dẫn tỷ lệ thuận với hiệu điện thế đặt vào hai đầu dây dẫn. Nên ta có:
U1/U2 = I1/I2 => 12/36 = 0,5/I2 => I2 = 36.0,5/12 = 72/12 = 1,5A
Vậy cường độ dòng điện chạy qua nó là 1,5A
Bài tập 3: Một nguồn điện có điện trở trong 0,1Ω được mắc với điện trở 4,8Ω thành mạch kín. Khi đó hiệu điện thế giữa hai cực của nguồn điện là 12 (V). Cường độ dòng điện trong mạch là bao nhiêu ?
Hướng dẫn cách giải:
Cường độ dòng điện trong mạch là:
I = UN / R = 12 : 4,8 = 2,5A
Vậy cường độ dòng điện có trong mạch là: 2,5A
Bài tập 4: Cho mạch điện đơn giản: Nguồn 1 chiều 24V, điện trở 12Ω. Tính các tham số liên quan đến mạch điện như hình 3.2 dưới đây:
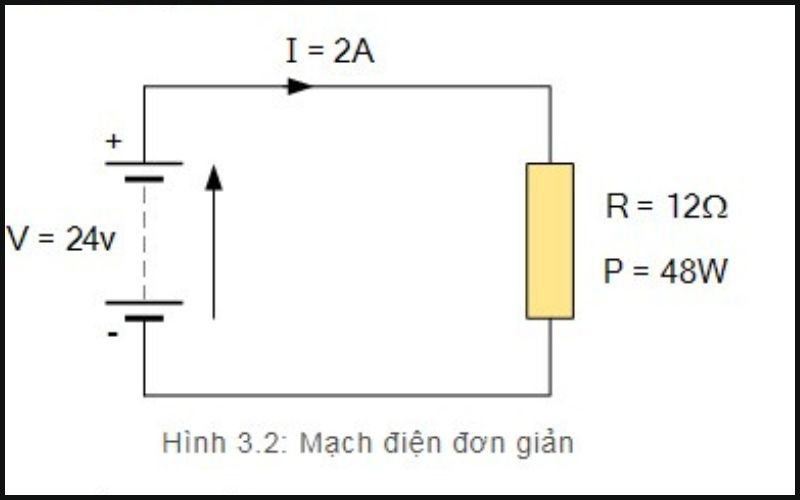
Hình 3.2 Mạch điện đơn giản
Hướng dẫn cách giải:
Khi đó, các tham số liên quan đến mạch điện được tính như sau:
- Điện áp rơi trên điện trở R là: U=I.R= 2.12 =24V
- Dòng điện: I=U/R= 24/12 = 2A
- Điện trở: R=U/I= 24/2 = 12Ω
- Công suất điện: P=U.I= 24.2 = 48W
Như vậy, công suất của mạch chỉ xuất hiện khi có cả điện áp và dòng điện. Với trường hợp hở mạch, khi đó dòng điện bằng 0, công suất P=U.I= 24.0 = 0. Nếu trường hợp ngắn mạch xảy ra thì điện áp bằng 0, công suất P=U.I= 0.I= 0.
Bài tập 5: Một bóng đèn thắp sáng có điện trở 12Ω và cường độ dòng điện chạy qua dây tóc bóng đèn là 0,5A. Tính hiệu điện thế giữa hai đầu dây tóc bóng đèn khi đó.
Hướng dẫn cách giải:
Theo định luật ôm, ta có: I=U/R => U=I.R
Hiệu điện thế giữa hai đầu dây tóc bóng đèn:
U=I.R = 0,5 .12 = 6V
Vậy hiệu điện thế giữa hai đầu dây bóng đèn là 6V
Bài tập 6: Đặt cùng một hiệu điện thế vào đầu dây dẫn có điện trở R1 và R2 = 3R1. Dòng điện chạy qua dây dẫn nào có cường độ lớn hơn và lớn hơn bao nhiêu lần?
Hướng dẫn cách giải:
Ta có: I1= U/R1; I2= U/R2 = U/3R1
=> I2/I1 = (U/3R1)/(U/R1)
<=> I2= I1/3
<=> I1=3I2
Vậy dòng điện chạy qua dây dẫn I1 có cường độ lớn hơn và lớn hơn 3 lần.
- Xem thêm:
- Điện trở là gì? Tính chất và công thức tính điện trở đầy đủ và chi tiết
- Sơ đồ nguyên lý là gì? Sơ đồ lắp đặt là gì? Cách vẽ và ví dụ minh họa
- Tổng hợp 7 đề thi Vật lý lớp 7 giữa học kì 1 2022-2023 có đáp án (Tải nhiều)
Trên đây là những thông tin về định luật ôm mà bạn cần nắm vững để có thể học tốt môn vật lý. Hy vọng thông qua bài viết sẽ một phần nào đó giúp các bạn hiểu được như thế nào là khái niệm, ý nghĩa, công thức và các dạng bài tập về định luật ôm. Để từ đó có thể dễ dàng làm các bài tập hoặc bài kiểm tra liên quan đến định luật ôm một cách nhanh hơn. Chúc các bạn học tốt và đạt kết quả cao trong môn vật lý!
Cách viết cấu hình Electron và xác định electron đơn giản nhất
Electron là một nền tảng kiến thức cơ bản trong lĩnh vực hóa học. Để chắc chắn rằng bạn sẽ không bị “mất gốc” và luôn có thể hiểu bài thì đừng quên nắm chắc cho mình kiến thức về electron nhé! Tại bài viết này, Bamboo School sẽ giúp các nắm rõ các kiến thức và lý thuyết về electron, cùng với đó sẽ là một số mẹo giúp các bạn học sinh dễ dàng ghi nhớ và viết được cấu hình electron. Hãy theo dõi thật kỹ bài viết sau đây để không bỏ lỡ mảng kiến thức nào nhé!
Electron là gì? Khái niệm lý thuyết về electron
Electron chính là các hạt bao quanh hạt nhân và chúng mang điện tích âm. Vật chất được cấu thành từ những nguyên tử, bên trong những hạt nguyên tử này sẽ là một hạt nhân với điện tích dương và các hạt electron bao bọc bên ngoài nó.
Cấu tạo một nguyên tử
Thuyết electron
Thuyết này chính là dựa vào sự cư trú và di chuyển của các hạt electron nhằm giải thích các hiện tượng điện và các tính chất điện của các vật. Nội dung của thuyết electron như sau:
- Electron có thể rời khỏi nguyên từ để di chuyển từ nơi này sang nơi khác trong phạm vi thể tích của vật dẫn. Trong trường hợp này, nguyên tử bị mất đi electron sẽ trở thành hạt mang điện dương (còn gọi là ion dương)
- Một nguyên tử trung hòa (không mang điện) có thể nhận thêm electron và nó sẽ trở thành hạt mang điện âm (còn gọi là ion âm)
- Một vật thể nhiễm điện âm khi nó có số electron nhiều hơn số proton. Và nếu ngược lại thì nó sẽ mang điện dương.
Các electron di chuyển giữa các nguyên tử
Cấu hình electron nguyên tử
Trong một nguyên tử, các electron đều sẽ được phân chia ra theo từng lớp và chúng sẽ mang năng lượng riêng. Và cụ thể, electron trong một phân tử cơ bản sẽ được phân bổ như sau:
- Chúng luôn được sắp xếp theo mức năng lượng tăng dần.
- Có 7 bậc năng lượng (tăng dần từ 1 đến 7) và xếp theo thứ tự các lớp s, p, d, f.
- Với mức điện hạt nhân lớn hơn thì mức năng lượng 4s sẽ thấp hơn 3d.
- Số electron tối đa có thể xếp ở mỗi phân lớp sẽ là s2, p6, d10, f14.
- Số electron tối đa được xếp ở mỗi lớp thứ n là 2n2 với n = 1, 2, 3, 4.
Bảng mức năng lượng cấu hình electron
| Số thứ tự lớp (n) | 1 | 2 | 3 | 4 |
| Tên của lớp | K | L | M | N |
| Số electron tối đa | 2 | 8 | 18 | 32 |
| Số phân lớp | 1 | 2 | 3 | 4 |
| Kí hiệu phân lớp | 1s | 2s 2p | 3s 3p 3d | 4s 4p 4d 4f |
| Số electron tối đa ở phân lớp và ở lớp | 2 | (2,6) → 8 | (2, 6, 10) → 18 | (2, 6, 10, 14) → 32 |
Ngoài các lớp K, L, M, N thì còn có các lớp O, P, Q,… cho tới khi các electron được sắp xếp đủ vào các lớp.
Đặc điểm lớp electron ngoài cùng
Các electron lớp ngoài cùng chính là yếu tố quyết định nên tính chất hóa học của một nguyên tố.
- Số electron lớp ngoài cùng của nguyên tử mỗi nguyên tố là tối đa 8 electron (8e). Các nguyên tử nào có cho mình 8e lớp ngoài cùng đều rất bền vững và hầu như không tham gia vào các phản ứng hóa học. Thông thường đó sẽ là các nguyên tử khí hiếm (ngoại trừ He với 2e lớp ngoài cùng).
- Nguyên tử kim loại: có 1, 2, 3e lớp ngoài cùng (trừ H, He và B)
- Nguyên tố phi kim: thường có 5, 6, 7e lớp ngoài cùng.
- Nguyên tử kim loại hoặc phi kim: có 4e lớp ngoài cùng.
Cách viết cấu hình Electron
Để viết được một cấu hình electron hoàn chỉnh của một nguyên tố hóa học, chúng ta có 3 bước cụ thể sau đây:
- Bước 1: Xác định số e (electron) của nguyên tử (Z).
Ví dụ: nguyên tử Na có số tổng số electron là 11 (Z = 11).
- Bước 2: Sắp xếp các e theo thứ tự tăng dần mức năng lượng.
1s22s22p63s23p64s23d104p6…
Ví dụ: đối với nguyên tố Na có Z = 11 → 1s22s22p63s2
- Bước 3: Sắp xếp cấu hình e: theo thứ tự từng lớp (1→7), trong mỗi lớp theo thứ tự từng phân lớp (s→p→d→f).
Ví dụ: Na (Z = 11) → 1s22s22p63s1
Nguyên lý viết cấu hình electron nguyên tử
Để viết được chính xác cấu hình electron của một nguyên tử, điều trước tiên ta cần phải xác định được đúng số hạt electron mà nguyên tử này có (kiểm tra qua bảng tuần hoàn hóa học). Và điều quan trọng tiếp theo là các bạn cần phải nắm rõ và thuộc được mức năng lượng cấu hình electron và số electron ở mỗi lớp.
Số electron của mỗi nguyên tử là khác nhau
Tuy nhiên cũng đừng quá lo lắng nhé! BamBoo School đã chuẩn bị một số mẹo học cấu hình electron ở bên dưới cho các bạn học sinh đấy!
Các bước viết cấu hình electron
Cấu hình electron sẽ được viết trong 3 bước đơn giản như đã hướng dẫn cụ thể bên trên.
- Bước 1: Xác định số e của nguyên tử cần viết cấu hình.
- Bước 2: Sắp xếp các e này theo thứ tự tăng dần mức năng lượng.
- Bước 3: Sắp xếp cấu hình e cho phù hợp.
Mẹo viết cấu hình electron
Một mẹo đơn giản để viết được cấu hình electron đó là ghi nhớ
(thứ tự tăng mức năng lượng của các phân lớp). Tuy nhiên để đơn giản hóa quá trình này, BamBoo School đã chuẩn bị một sơ đồ thu gọn dành cho các bạn học sinh.

Quy tắc Klechkowski
Bạn chỉ cần ghi nhớ bảng cấu hình electron cụ thể sau đây và thứ tự di chuyển của mũi tên là sẽ không bị nhầm lẫn giữa các bậc năng lượng!
Cách viết cấu hình electron rút gọn
Một nguyên tử có nhiều electron sẽ có cấu hình electron tương đối phức tạp và dài. Vậy nên cách viết cấu hình electron rút gọn ra đời với mục đích thu gọn cấu hình và ta có thể dễ dàng đọc được cấu hình được viết hơn.
Để dễ hình dung, thao tác này được hiểu là thay thế các lớp năng lượng đầu tiên của nguyên tử bằng tên của một nguyên tử khác có cấu hình tương đương.
Ví dụ:
Cl (Z = 17): 1s22s22p63s23p5
⇒ Cl: [Ne]3s23p5
Trước tiên, bạn cần nắm chắc cấu hình của một số nguyên tố cơ bản như sau:
- Hidro (Z = 1): 1s1
- Heli (Z = 2): 1s2 đã bão hòa.
- Liti (Z = 3): 1s22s1
- Neon (Z = 10): 1s22s22p6
- Và một số nguyên tố cơ bản khác
Bước 1: Xác định số e của nguyên tử cần viết cấu hình.
Bước 2: Sắp xếp các e này theo thứ tự tăng dần mức năng lượng.
Bước 3: Sắp xếp cấu hình e cho phù hợp.
Bước 4: Thay thế cấu hình electron phía trước bằng các nguyên tố có cấu hình tương đương.
Cách xác định electron nguyên tử
Số electron của mỗi nguyên tử là cố định và luôn được đề cập trong các bản nguyên tố hóa học. Vậy nên để xác định được số electron của một nguyên tử thì bạn hãy dò bản nguyên tố hóa học nhé!

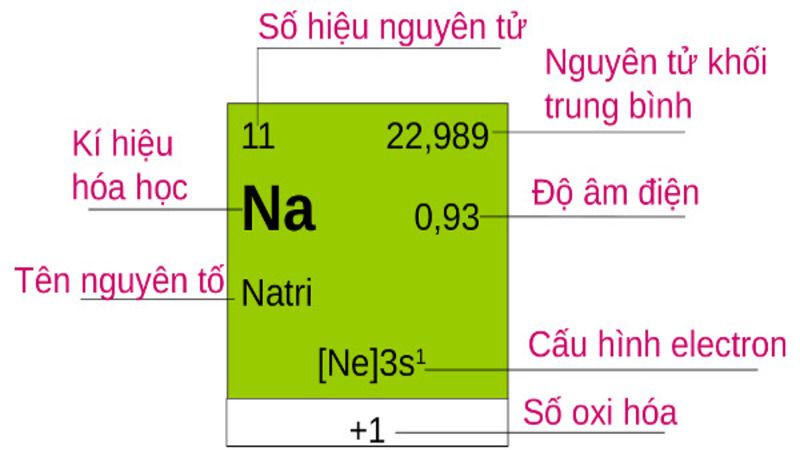
Ý nghĩa các con số của một nguyên tố hóa học trong bảng tuần hoàn
Bảng cấu hình electron nguyên tử của 20 nguyên tố thường gặp nhất
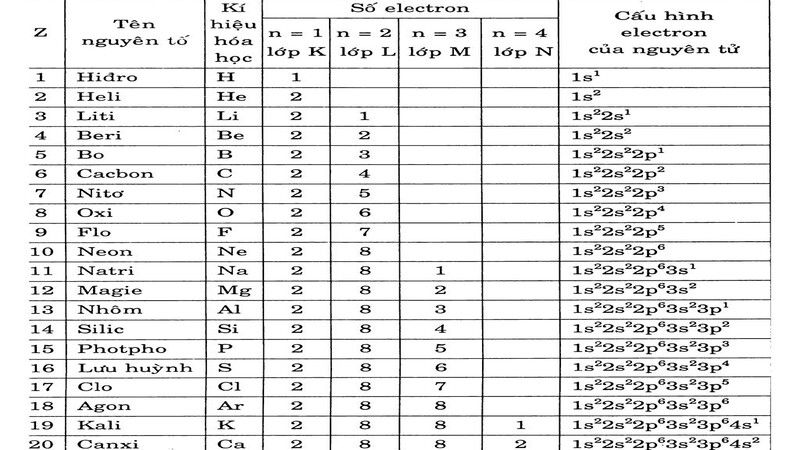
Bài tập về Electron có đáp án
Bài tập 1: Nguyên tử X có ký hiệu 2656X. Cho các phát biểu sau về X:
(1) Nguyên tử của nguyên tố X có 8 electron ở lớp ngoài cùng.
(2) Nguyên tử của nguyên tố X có 30 notron trong hạt nhân.
(3) X là một phi kim.
(4) X là nguyên tố d.
Trong các phát biểu trên, những phát biểu đúng là?
A. (1), (2), (3) và (4).
B. (1), (2) và (4).
C. (2) và (4).
D. (2), (3) và (4).
Hướng dẫn:
Do có sự chèn mức NL nên electron được phân bố như sau:
1s22s22p63s23p64s23d6
Cấu hình electron của X: 1s22s22p63s23p63d64s2hay [Ar] 3d64s2
– Số e lớp ngoài cùng là 2 do đó X là Kim loại
– N = A – Z = 56 – 26 = 30
– Electron cuối cùng phân bố trên phân lớp 3d nên X là nguyên tố d.
⇒ Chọn C.
Bài tập 2: Cấu hình electron nào sau đây viết sai?
A. 1s22s22p5
B. 1s22s22p63s23p64s1
C. 1s22s22p63s23p64s24p5
D. 1s22s22p63s23p63d34s2
Hướng dẫn:
Cấu hình 1s22s2p63s23p64s24p5 thiếu phân lớp 3d. Trước khi electron được điền vào phân lớp 4p phải điền vào phân lớp 3d.
⇒ Chọn C.
Bài tập 3: Một nguyên tố d có 4 lớp electron, phân lớp ngoài cùng đã bão hòa electron. Tổng số electron s và electron p của nguyên tố này là
Hướng dẫn:
Nguyên tố d có 4 lớp electron → electron cuối cùng trên phân lớp 3d.
Cấu hình electron của nguyên tố này có dạng: 1s22s22p63s23p63dX4s2.
Vậy tổng số electron s và electron p là 20
Bài tập 4: Nguyên tử nguyên tố Y có số khối là 16. Trong hạt nhân của Y, số hạt mang điện bằng số hạt không mang điện. Cấu hình electron của Y là
A 1s22s22p4.
B 1s22s22p63s23p4.
C 1s22s22p6.
D 1s22s22p63s23p6.
Đáp án: A
– Số khối: A = Z + N
– Hạt nhân chứa p (mang điện) và n (không mang điện)
– Nguyên tử nguyên tố Y có số khối là 16 → Z + N = 16 (1)
– Trong hạt nhân của Y, số hạt mang điện bằng số hạt không mang điện → Z = N (2)
Giải (1) và (2) ⟹ Z = N = 8
→ Cấu hình e của Y: 1s22s22p4
Bài tập 5: Một nguyên tử của nguyên tố X có 3 lớp electron. Lớp ngoài cùng có 4 electron. Xác định số hiệu nguyên tử của X. Viết cấu hình e của X
Hướng dẫn:
Z = 2 + 8 + 4 = 14
Cấu hình e của X là 1s22s2p63s23p2
Xem thêm:
- Este là gì? Tính chất vật lý, hóa học và công thức cấu tạo của hợp chất este
- C là gì trong hóa học? Khái niệm, công thức tính C và các bài tập ví dụ có đáp án
- Tính chất hóa học đặc trưng của kim loại là gì? Ví dụ tính chất hóa học kim loại
Bên trên là tổng hợp những kiến thức cơ bản của electron và cách viết cấu hình electron của một phân tử. Mong rằng bài viết này sẽ hỗ trợ quá trình học tập của các bạn học sinh. Và các bạn cũng đừng quên ôn và luyện tập các dạng bài về electron thật nhuần nhuyễn để nắm vững mảng kiến thức này nhé!
Lời dẫn trực tiếp là gì? Lời dẫn gián tiếp là gì? Dấu hiệu nhận biết và ví dụ
Lời dẫn trực tiếp là gì? Lời dẫn gián tiếp là gì? Làm thế nào để nhận biết lời dẫn trực tiếp, lời dẫn gián tiếp? Nếu các em học sinh vẫn còn loay hoay không biết cách phân biệt các mẫu câu này, hãy cùng theo dõi bài viết sau của Bamboo School để hiểu rõ hơn điểm ngữ pháp tiếng Việt này nhé!
Lời dẫn trực tiếp là gì?
Lời dẫn trực tiếp là nhắc lại nguyên văn lời nói, suy nghĩ của nhân vật hoặc một người nào đó. Lời dẫn trực tiếp thường được đặt trong dấu ngoặc kép.
Ví dụ: Tục ngữ có câu: “Lá lành đùm lá rách”.
Ví dụ: Hoạ sĩ nghĩ thầm: “Khách tới bất ngờ, chắc cu cậu chưa kịp quét tước dọn dẹp, chưa kịp gấp chăn chẳng hạn”. (Nguyễn Thành Long)

Lời dẫn gián tiếp là gì?
Lời dẫn gián tiếp là thuật lợi lời nói hay nêu lại ý nghĩ của người hoặc nhân vật. Lời dẫn gián tiếp sẽ có những điều chỉnh thích hợp trong đoạn văn và chúng không đặt trong dấu ngoặc kép.
Ví dụ: Thúy Ngân bảo ngày mai bạn ấy không đến được
Ví dụ: Thầy giáo dặn chúng tôi về ôn bài, mai có giờ kiểm ưa.
Tác dụng của lời dẫn trực tiếp và lời dẫn gián tiếp
Như bạn đã biết về khái niệm lời dẫn trực tiếp và lời dẫn gián tiếp ở trên. Dựa vào định nghĩa ta cũng nhận biết được tác dụng của mỗi loại câu này là làm gì. Cụ thể như sau:
- Lời dẫn trực tiếp sẽ có tác dụng nhắc lại nguyên văn lời nói, ý nghĩa của người hoặc nhân vật. Chúng ta dùng lời dẫn trực tiếp để trích lại toàn bộ những gì nhân vật đã nói.
- Lời dẫn gián tiếp sẽ có tác dụng thuật lại lời nói và ý nghĩa của người hoặc nhân vật, có điều chỉnh thích hợp trong ngữ cảnh nói. Trường hợp chúng ta muốn tường thuật lại câu chuyện có nhắc đến câu nói của người khác, bạn có thể dùng lời dẫn gián tiếp để diễn tả.
Dấu hiệu nhận biết lời dẫn trực tiếp
Dấu hiệu nhận biết lời dẫn trực tiếp rất đơn giản. Bạn chỉ cần quan tâm đến các đặc điểm là câu dẫn được đặt trong dấu ngoặc kép, sau dấu 2 chấm.
Ví dụ:
Hôm nay Nam đến trường rất sớm, bác bảo vệ thấy thế bèn hỏi: “Sao cháu đi sớm thế?”
Mẹ ra ngoài và dặn lại các con: “Đừng cho bé Su ra ngoài đường nhé!”
Dấu hiệu nhận biết lời dẫn gián tiếp
Khác với lời dẫn trực tiếp, lời dẫn gián tiếp sẽ không được đặt trong dấu ngoặc kép mà sẽ được diễn đạt hài hòa cùng với lời văn người dẫn. Chúng ta không cần trích dẫn y nguyên lời nói của nhân vật. Thay vào đó ta có thể thay đổi, điều chỉnh phù hợp ngay lúc thuật lại.
Ví dụ:
Hôm nay Nam đi học rất sớm, đi đến cổng trường bèn bị bác bảo vệ hỏi rằng sao lại đi sớm thế.
Mẹ đi ra ngoài và dặn lại các con rằng không cho bé Su chạy ra ngoài đường.
Cách dẫn trực tiếp và cách dẫn gián tiếp
Trong giao tiếp hằng ngày hoặc khi kể chuyện bằng lời nói, cách dẫn trực tiếp ít được sử dụng hơn. Thay vào đó, việc dùng cách dẫn gián tiếp sẽ trở nên phổ biến và giúp người nói thể hiện được tốt câu chuyện theo cá tính của mình.
Ngược lại, trong các tác phẩm văn chương như truyện, tiểu thuyết, tác giả thường dùng các lời dẫn trực tiếp để dẫn thoại nhân vật. Các lời dẫn này được đánh dấu bằng gạch đầu dòng ở đầu mỗi câu.

Cách chuyển lời dẫn trực tiếp sang gián tiếp
Khi chuyển lời dẫn trực tiếp sang gián tiếp ta sẽ phải bỏ bớt một số từ cảm thán và dấu câu “đối với văn bản viết”. Ở lời dẫn gián tiếp ta sẽ điều chỉnh một số từ ngữ cho phù hợp với ngữ cảnh nói. Ví dụ chuyển đổi câu sau từ lời dẫn trực tiếp sang lời dẫn gián tiếp:
Có câu: “Chúng ta phải ghi nhớ công lao của các vị anh hùng dân tộc, vì các vị ấy là tiêu biểu của một dân tộc anh hùng.”
– Chuyển câu gián tiếp sẽ là: Chủ tịch Hồ Chí Minh đã từng nói phải ghi nhớ công lao của các vị anh hùng dân tộc, vì các vị ấy là tiêu biểu của một dân tộc anh hùng.
=> Có sự khác biệt (lược bỏ) so với câu gốc trực tiếp của chủ tịch Hồ Chí Minh, đó là loại bỏ cụm động từ “chúng ta phải”.
Ví dụ và bài tập vận dụng về lời dẫn gián tiếp, trực tiếp
Đọc các đoạn trích sau và trả lời câu hỏi.
a) Lão tìm lời lẽ giảng giải cho con trai hiểu. Lão khuyên nó hãy dằn lòng bỏ đám này, để dùi giắng lại ít lâu, xem có đám nào khá mà nhẹ tiền hơn sẽ liệu; chẳng lấy đứa này thì lấy đứa khác; làng này đã chết hết gái đâu mà sợ.
(Nam Cao, Lão Hạc)
b) Nhưng chớ hiểu lầm rằng Bác sống khắc khổ theo lối nhà tu hành, thanh tao theo kiểu nhà hiền triết ẩn dật.
(Phạm Văn Đồng, Chủ tịch Hồ Chí Minh, tinh hoa và khí phách của dân tộc, lương tâm của thời đại).
Trong đoạn trích (a), bộ phận im đậm là lời nói hay ý nghĩa? Nó có được ngăn cách với bộ phận đứng trước bằng dấu gì không?
Trong đoạn trích (b), bộ phận im đậm là lời nói hay ý nghĩa? Giữa bộ phận in đậm và bộ phận đứng trước có từ gì? Có thể thay từ đó bằng từ gì?
Trả lời
Trong đoạn trích (a), bộ phận in đậm là lời nói của nhân vật. Đây là nội dung của lời khuyên như có thể thấy ở từ “khuyên” trong phần lời của người dẫn. Nó không được ngăn cách với phần câu đứng trước bằng một loại dấu cụ thể nào. Trước phần này có thể đặt thêm từ rằng hoặc từ là sau từ nó.
Trong đoạn trích (b), bộ phận in đậm là ý nghĩ của nhân vật, vì trước đó có từ “hiểu”. Giữa phần ý nghĩa được dẫn và phần lời của người dẫn có từ “rằng”. Có thể thay từ “là” vào vị trí của từ “rằng” trong trường hợp này.
Câu 2:
Tìm lời dẫn trong những đoạn trích (trích từ truyện ngắn Lão Hạc của Nam Cao. Cho biết đó là lời nói hay ý nghĩ được dẫn, là lời dẫn trực tiếp hay gián tiếp?
Nó cứ làm in như nó trách tôi; nó kêu ư ử, nhìn tôi, như muốn bảo rằng: “A! Lão già tệ lắm! Tôi ăn ở với Lão như thế mà lão đối xử với tôi như thế này à?”.
Sau khi thằng con đi, lão tự bảo rằng : “Cái vườn là của con ta. Hồi còn mồ ma mẹ nó, mẹ nó cố thắt lưng buộc bụng, dè sẻn mãi, mới để ra được năm mươi đồng bạc tậu. Hồi ấy, mọi thứ còn rẻ cả…”
Trả lời
– Đoạn (a): Phần trong ngoặc kép
(“A! lão già… thế này à?”)
là lời dẫn trực tiếp – dẫn lời (qua ý nghĩ của nhân vật gắn cho con chó).
– Đoạn (b): Phần trong ngoặc kép
(“Cái vườn… còn rẻ cả…”)
là lời dẫn trực tiếp – dẫn ý.
Xem thêm:
- Nói giảm nói tránh là gì? Tác dụng, ví dụ và cách nói giảm nói tránh
- Thành phần biệt lập là gì? Các loại thành phần biệt lập và ví dụ minh họa
- Phương thức biểu đạt là gì? Có bao nhiêu loại? Cách xác định và nhận biết
Mong rằng những chia sẻ về lời dẫn gián tiếp là gì và lời dẫn trực tiếp là gì trên đây sẽ hữu ích cho các bạn. Chúc bạn học tốt!
Biến dị tổ hợp là gì? Nguyên nhân, ý nghĩa, ví dụ và cách tính biến dị tổ hợp
Hãy cùng Bamboo School tìm hiểu kiến thức về biến dị tổ hợp là gì? Có những nguyên nhân nào gây ra biến dị tổ hợp? Ý nghĩa của biến dị tổ hợp trong thực tiễn? Tất cả sẽ được giải đáp trong bài viết sau.
Khái niệm biến dị tổ hợp là gì?
Hiểu một cách đơn giản thì biến dị tổ hợp chính là kiểu tổ hợp các tính trạng của cá thể bố và cá thể mẹ trong quá trình sinh sản. Trong đó, các tổ hợp đột biến có thể được sinh ra từ sự phân li độc lập của các yếu tố di truyền (cụ thể là nhiễm sắc thể) và sự liên kết ngẫu nhiên của chúng trong quá trình thụ tinh. Sự liên kết này cũng chính là cơ chế làm phát sinh biến dị tổ hợp.
Biến dị tổ hợp trong tự nhiên rất phong phú và đa dạng. Tuy nhiên, ta vẫn có thể dự đoán trước được kích thước cũng như tần suất xuất hiện của biến dị tổ hợp, từ đó kịp thời điều chỉnh hoặc can thiệp vào quá trình phát sinh giao tử và quá trình thụ tinh.

Biến dị tổ hợp là kiểu tổ hợp các tính trạng của cá thể bố và cá thể mẹ trong quá trình sinh sản
Nguyên nhân biến dị tổ hợp
Sau khi hiểu được biến dị tổ hợp là gì, chúng ta sẽ cùng tìm hiểu nguyên nhân hình thành nên nó. Biến dị tổ hợp chủ yếu được phát sinh từ 3 nguyên nhân chính bao gồm:
- Quá trình phát sinh giao tử giữa cá thể đực và cá thể cái
- Quá trình thụ tinh
- Do hoán vị gen
Tuy nhiên, biến dị tổ hợp chỉ xuất hiện ở các loài sinh sản hữu tính. Đối với trường hợp sinh sản vô tính thì hầu hết không có biến dị tổ hợp, bởi vì nó chỉ có quá trình giảm phân mà không phát sinh quá trình thụ tinh.

Có 3 nguyên nhân chính hình thành nên biến dị tổ hợp ở các loài sinh sản hữu tính
Ý nghĩa của biến dị tổ hợp
Biến dị tổ hợp đóng một vai trò và ý nghĩa vô cùng quan trọng trong đời sống tự nhiên, là một phần không thể thiếu của tự nhiên. Đây được xem là nguồn biến dị của sinh vật, góp phần làm tăng tính đa dạng và phong phú của tất cả các chủng loại. Do đó, ta nói rằng, biến dị tổ hợp trở thành nguồn cung ứng không thể thiếu cho quá trình tiến hóa của các loài sinh vật.
Bên cạnh đó, người ta còn có thể phân tích những đặc điểm, dựa vào biến dị tổ hợp để lựa chọn giống phù hợp hoặc lai tạo giống mới. Nguyên do là bởi vì trong quá trình phát sinh giao tử và thụ tinh, cá thể con hoặc là kế thừa những tính trạng đã có sẵn trên cá thể bố và mẹ, hoặc là có thêm những tính trạng mới. Những cá thể có gen trội sẽ được giữ lại, đồng thời những cá thể có gen lặn sẽ bị bỏ qua.
Biến dị tổ hợp được ứng dụng phổ biến trong quá trình lai giống và chọn giống, nhằm chọn lọc những cá thể sở hữu gen trội
Ví dụ về biến dị tổ hợp
Dưới đây là một số ví dụ cơ bản về biến dị tổ hợp trong đời sống thực tiễn:
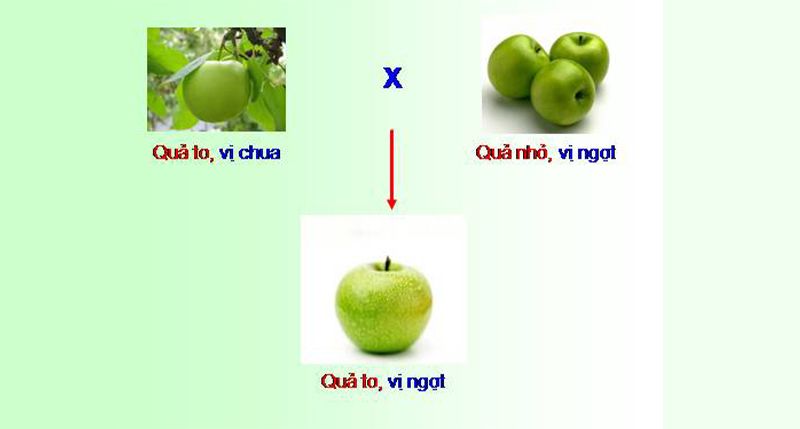
- Ví dụ 1: Cho 2 kiểu hình là hạt đậu màu vàng, vỏ trơn và hạt đậu màu xanh, vở nhăn. Sau khi lai giữa 2 kiểu hình trên, ta sẽ thu được các kiểu hình hoàn toàn mới là: Hạt vàng – vỏ nhăn, hạt xanh – vỏ trơn. Các kiểu hình mới, khác hẳn kiểu hình đã cho ban đầu chính là biến dị tổ hợp.
- Ví dụ 2: Bố có đặc điểm là mắt nhỏ, mũi thấp. Mẹ có đặc điểm là mắt to, mũi cao. Con gái sở hữu đặc điểm di truyền từ bố và mẹ là mắt nhỏ, mũi cao. Như vậy, con gái chính là biến dị tổ hợp.
- Ví dụ 3: Cá thể đực là quạ đen, cá thể cái là quạ khoang. Các con của chúng là con lai, màu lông sở hữu những đặc điểm di truyền từ cả bố và mẹ. Ta nói đây chính là trường hợp biến dị tổ hợp.

Một số ví dụ thường gặp về biến dị tổ hợp trong đời sống thực tiễn
Các biến dị tổ hợp được tạo ra
Biến dị chính là sự thay đổi về kiểu hình của cá thể sinh vật, làm cho nó khác với những cá thể khác trong một quần thể nào đó. Trong biến dị có 2 loại là biến dị di truyền và biến dị không di truyền. Biến dị tổ hợp là một phần của biến dị di truyền.
Về cơ bản, trong biến dị tổ hợp, các tính trạng, vật chất di truyền, kiểu gen ở đời con sẽ được sắp xếp lại từ những tính trạng đã có sẵn ở đời bố mẹ. Cá thể mới được hình thành có thể sở hữu những đặc điểm tương tự với bố mẹ, hoặc có thể lai tạo, hình thành nên tính trạng mới.
Trong biến dị tổ hợp, các tính trạng, vật chất di truyền ở đời con sẽ được sắp xếp lại từ những tính trạng đã có từ đời bố mẹ
Cách tính số loại biến dị tổ hợp
Cách tính biến dị tổ hợp được thực hiện như sau:
- Đầu tiên, ta phải lần lượt xét từng cặp gen theo các tính trạng đã được nêu ở đề bài
- Sau đó, ta tính tỉ lệ kiểu hình giống đời bố và mẹ từ những cặp gen trên
- Cuối cùng, ta tính tỉ lệ xuất hiện biến dị tổ hợp ở đời con bằng cách lấy 1 trừ cho tỉ lệ kiểu hình giống đời bố và mẹ
Ví dụ: Cho phép lai P : AaBbDdEe x aaBbDDEe, biết mỗi gen quy định một tính trạng, ko lập bảng hãy tính
a/ số loại biến dị tổ hợp ớ đời con F1.
b/ tỉ lệ KH mang 3 tính trạng trội ở đời con F1
Giải:
a, Aa x aa tạo 2 loại KH 1 trội : 1 lặn.
Bb x Bb tạo 2 loại KH 3 trội : 1 lặn.
DD x Dd chỉ tạo KH trội.
Ee x Ee tạo 2 loại KH 3 trội : 1 lặn.
Số KH tạo ra: 2 x 2 x 2 = 8
Có 2 KH giống bố mẹ, vậy còn 6 kiểu hình không giống bố mẹ, nên có 6 loại biến dị tổ hợp.
b, Tỉ lệ mang 3 tính trạng trội ở con:
(Có 2 TH là kiểu hình A,a là trội và kiểu hình A,a là lặn)
A_…. + aa….. = 0,5 x 0,75 x 0,25 x 2 + 0,75 x 0,75 x 0,5 = 46,875%
Tính tỉ lệ xuất hiện biến dị tổ hợp ở thế hệ sau
Xem thêm:
- Tổng hợp 5 bộ đề thi sinh lớp 8 giữa học kì 1 2022-2023 có đáp án (kèm file tải)
- Este là gì? Tính chất vật lý, hóa học và công thức cấu tạo của hợp chất este
- Từ đồng âm là gì? Phân loại, cách nhận biết và bài tập về từ đồng âm
Trên đây là một số đặc điểm, nguyên nhân hình thành biến dị tổ hợp và cách tính biến dị tổ hợp mà bạn có thể áp dụng vào một số dạng bài tập. Hy vọng qua bài viết này, các bạn đã phần nào hiểu được biến dị tổ hợp là gì, cũng như tầm quan trọng và ý nghĩa của nó trong đời sống thực tiễn. Đừng quên theo dõi để cập nhật thêm nhiều kiến thức bổ ích tại địa chỉ bambooschool.edu.vn các bạn nhé!

