Bộ đề cương ôn tập học kỳ 2 môn toán lớp 12

Đề cương ôn tập học kỳ 2 môn toán lớp 12 là tài liệu vô cùng quan trọng dành cho các em học sinh ôn tập để thi cho kỳ thi cuối năm. Đề cương ôn tập thi học kì 2 lớp 12 môn toán được biên soạn rất chi tiết, cụ thể với những dạng bài tập, lý thuyết được trình bày một cách chi tiết, khoa học. Mời các em học sinh theo dõi nội dung chi tiết Đề cương Toán 12 học kì 2 tại đây.

Đề cương ôn tập thi học kì 2 lớp 12 môn toán phần giải tích

Gồm lý thuyết và bài tập của các phần: số phức, nguyên hàm, tích phân và ứng dụng, giúp các em học sinh ôn tập và nâng cao kiến thức môn Toán giải tích hiệu quả. Từ đó có một kiến thức nền tốt và chuẩn bị đầy đủ cho bài thi cuối học kì 2 và luyện thi THPT Quốc gia 2022. Mời các bạn tham khảo các nội dung dưới đây.

Nguyên hàm

Phần Nguyên hàm học kỳ 2 Toán lớp 12 với bộ đề cương được chọn lọc có sẵn đáp án có trong Đề thi THPT Quốc gia. Các câu hỏi bao gồm những chủ đề như sau:

• Nguyên hàm của hàm số đa thức 
• Nguyên hàm của hàm số hữu tỉ 
• Nguyên hàm của hàm số chứa căn 
• Nguyên hàm của hàm số lượng giác  
• Nguyên hàm của hàm số mũ và logarit 
• Nguyên hàm tổng hợp 
• Các bài toán nguyên hàm có điều kiện 
• Nguyên hàm của hàm ẩn 
• Bài toán ứng dụng của nguyên hàm

>> Xem thêm: Phương pháp giải và ví dụ về Nguyên hàm

Ví dụ minh họa:

Bài 1: Tìm nguyên hàm của hàm số

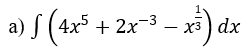
Hướng dẫn:

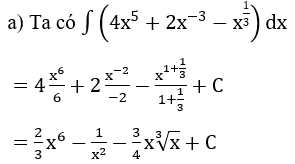
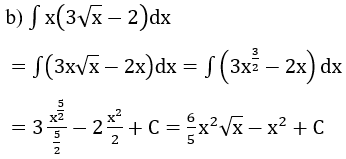
Bài 2: Tìm nguyên hàm của hàm số

Hướng dẫn:

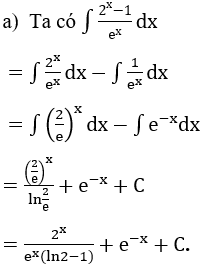
Bài 3: Tìm nguyên hàm bằng phương pháp đổi biến số

Hướng dẫn:

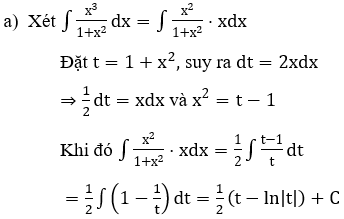
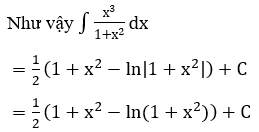
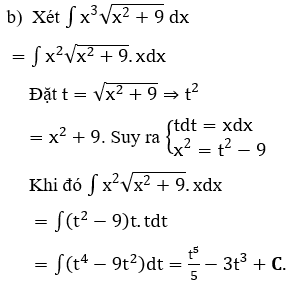
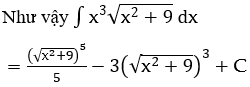
Bài 4: Tìm các họ nguyên hàm sau đây:

Hướng dẫn:

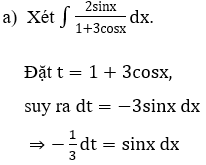
Vào Xem chi tiết để theo dõi các dạng bài Nguyên hàm hay nhất tương ứng:

[button size=”medium” style=”primary” text=”TẢI BỘ ĐỀ THI” link=”https://drive.google.com/drive/folders/1tkCX1kEwDeiQMNpK9xqu9AfIHLUMAlLa?usp=sharing” target=””]

Tích phân và ứng dụng

Khái niệm tích phân

Định nghĩa:

Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số: F(b) – F(a)

Được gọi là tích phân của f từ a đến b và kí hiệu: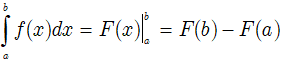

 

Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi

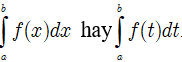
Tích phân đó chỉ phụ thuộc vào f và các cận a; b mà không phụ thuộc vào cách ghi biến số.

Định lí: Cho hàm số y = f(x) liên tục; không âm trên đoạn [a;b]. Khi đó, diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b là:

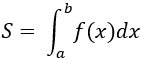
Tính chất của tích phân

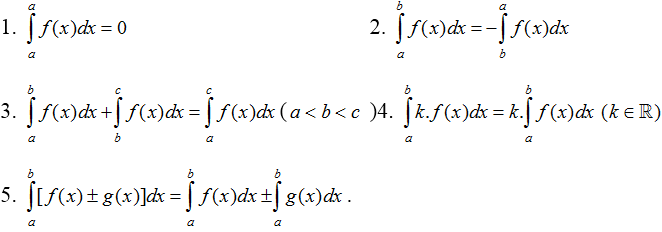
Ví dụ minh họa

1. Cho hàm số y = f(x) xác định và liên tục trên đoạn [-2; 4] biết rằng: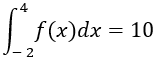

Tính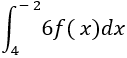

A. –60.     B. –30.     C. 60.     D. 20.

Lời giải

Ta có: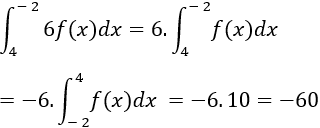

Chọn A.

Ví dụ 2. Cho hàm số: y = f(x) và y = g(x) xác định và liên tục trên đoạn [-3; 6]. Biết rằng:

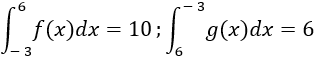
Tính: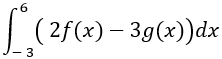

A. 2.     B. –38.     C. 38.     D. -2.

Lời giải

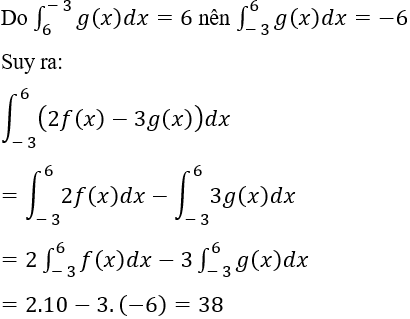
Chọn C.

[button size=”medium” style=”primary” text=”TẢI BỘ ĐỀ THI” link=”https://drive.google.com/drive/folders/1tkCX1kEwDeiQMNpK9xqu9AfIHLUMAlLa?usp=sharing” target=””]

Số phức

Trong tiếng Anh số’ phức có nghĩa là Complex Number. Từ complex cũng có nghĩa là phức hợp. Có nghĩa sô’ phức bao gồm nhiều thành phần để cấu tạo nên nó. Cụ thể tập số’ phức gồm các số’ có dạng a+bi. Trong đó a và b là các số thực và i là đơn vị ảo thỏa mãn i²=-1.

Cho hai số phức z = a + bi và z’ = a’ + b’i.

1. Phép cộng : z + z’ = a + a’ + (b + b’)i

Tính chất:

z + z’ = z’ + z, ∀z, z’ ∈ C (tính chất giao hoán)

(z + z’) + z” = z + (z’ + z”), ∀z’, Z” ∈ C (tính chất kết hợp)

z + 0 = 0 + z, ∀z ∈ C

-z = -a – bi là số phức đối của z = a + bi và z + (-z) = (-z) + z = 0.

2. Phép trừ : z – z’ = z + (- z’) = a – a’ + (b – b’)i

Phép cộng và phép trừ hai số phức có thể biểu diễn hình học bằng phép cộng và phép trừ vectơ trong mặt phẳng phức.

3. Phép nhân : z.z’ = aa’ – bb’ + (ab’ + a’b)i

Tính chất:

z.z’ = z’.z, ∀z, z’ ∈ C (tính chất giao hoán)

(z.z’)z” = z(z’.z”), ∀z, z’, z” ∈ C (tính chất kết hợp)

1.z = z.1 = z, ∀z ∈ C

z(z’ + z”) = z.z’ + z.z”, ∀z, z’, z” ∈ C (tính chất phân phối của phép nhân đối với phép cộng)

k(a + bi) = ka + kbi (∀k  ∈ R).

Ghi chú:

a) Từ định nghĩa, trong việc cộng – trừ – nhân các số phức thì ngoài việc nhớ công thức, chúng ta có thể

cộng – trừ – nhân như trong số thực với lưu ý i2= -1.

b) i3 = -i ; i4 = 1 ; i4k = 1 ; i4k+1 = i ; i4k+2 = -1, i4k+3 = -i (k ∈ Z)

c) Số phức liên hợp :

z = a + bi và  = a – bi là hai số phức liên hợp với nhau và ta có:

d) Môđun của số phức :

Môđun của số phức z = a + bi là  trong mặt phẳng phức với M(a ; b).

Ta có z = 0 ⇔ |z| = 0.

4. Phép chia:

– Số phức nghịch đảo của số phức z khác 0 là: 

– Với z ≠ 0 thì 

Vậy trong thực hành để tìm  ta có thể chỉ cần nhân tử và mẫu cho số phức liên hợp của z.

Ví dụ minh họa

Dạng 1: Tìm số phức thỏa mãn đẳng thức.

Ví dụ 1: Tìm các số thực x, y sao cho đẳng thức sau là đúng:

a) 5x + y + 5xi = 2y – 1 + (x-y)i

b) (-3x + 2y)i + (2x – 3y + 1)=(2x + 6y – 3) + (6x – 2y)i

Hướng dẫn:

a) Ta xem xét mỗi vế là một số phức, như vậy điều kiện để 2 số phức bằng nhau là phần thực bằng phần thực, phần ảo bằng phần ảo.

Ta có: 5x + y = 2y – 1; 5x = x – y, suy ra x = -1/7; y = 4/7

b) Câu này tương tự câu trên, các bạn cứ việc đồng nhất phần thực bằng phần thực, phần ảo bằng phần ảo là sẽ tìm ra được đáp án.

Ví dụ 2: Tìm số phức biết: 

a) |z| = 5 và z = z

b) |z| = 8 và phần thực của z bằng 5 lần phần ảo của z.

Hướng dẫn:

a) Giả sử z = a + bi, suy ra z = a – bi . Khi đó:

a2 + b2 = 52; a = a; b = -b (do z = z)

suy ra b = 0, a = 5

Vậy có 2 số phức z thỏa đề bài là z = 5 và z = -5

b) Hướng đi là lập hệ phương trình bậc nhất hai ẩn, từ đó giải tìm ra được phần thực và phần ảo của z.

Như vậy, cách để giải quyết dạng này là dựa vào các tính chất của số phức, ta lập các hệ phương trình để giải, tìm ra phần thực và ảo của số phức đề bài yêu cầu.

Dạng 2: Căn bậc hai và phương trình số phức.

Cho số phức z = a + bi, số phức w = x + yi được gọi là căn bậc hai của z nếu w2 = z, hay nói cách khác:

(x + yi)2 = a + bi

=> x2 – y2 + 2xyi = a + bi

=> x2 – y2 = a, 2xy=b(*).

Như vậy để tìm căn bậc 2 của một số phức, ta sẽ giải hệ phương trình (*) ở đã nêu ở trên.

Ví dụ: Tìm giá trị của m để phương trình sau z + mz + i = 0 có hai nghiệm z1 , z2 thỏa đẳng thức z1 2 + z2 2 = -4i.

Hướng dẫn:

Chú ý, đối với phương trình bậc 2 thì hệ thức Vi-et về nghiệm luôn được sử dụng. Như vậy ta có: z1 + z2 = -m, z1z2 = i.

Theo đề bài:

z1 2 + z2 2 = -4i 

=> (z1 + z2)2 – 2z1z2 = -4i

=> m2 = -2i.

Đến đây, bài toán qui về tìm căn bậc hai cho 1 số phức. Áp dụng phần kiến thức đã nêu ở trên, ta giải hệ sau: gọi m=a+bi, suy ra ta có hệ:

a2 + b2 = 0, 2ab = -2i

=> (a,b) = (1,-1) hoặc (a,b) = (-1,1).

Vậy có hai giá trị của m thỏa mãn đề bài.

>>Xem thêm: Lí thuyết và bài tập về số phức 

Đề cương ôn tập thi học kì 2 lớp 12 môn toán phần hình học

Trong chương trình hình học lớp 12, gồm lý thuyết, công thức, dạng toán hướng dẫn và bài tập có đáp án cụ thể bao gồm:

• Khái niệm hình đa diện, khối đa diện, ví dụ minh hoạ.
• Các phép dời hình trong không gian, định nghĩa hai hình bằng nhau.
• Khối đa diện lồi, khối đa diện đều, các loại khối đa diện đều (loại, tên gọi).
• Công thức tính thể tích khối lập phương, khối hộp chữ nhật, khối chóp, khối lăng trụ.
• Mặt tròn xoay: Mặt nón, hình nón, khối nón tròn xoay. Mặt trụ, hình trụ, khối trụ tròn xoay.
• Công thức tính diện tích xung quanh của hình nón tròn xoay, hình trụ tròn xoay. Công thức tính thể tích của khối nón tròn xoay, khối trụ tròn xoay.

Hình học giải tích trong không gian

Trong chương trình Hình học 12 phần hình học giải tích trong không gian bao gồm những phần như: 

• Hệ tọa độ trong không gian.
• Phương trình mặt phẳng trong hệ trục tọa độ Oxyz.
• Phương trình mặt cầu trong hệ trục tọa độ Oxyz.
• Phương trình đường thẳng trong hệ trục tọa độ Oxyz.

Ví dụ minh họa

Câu 1: Trong không gian Oxyz cho ba điểm A(1, 2,-1), B(2,-1,3), C(-4,7,5) tạo thành tam giác. Tìm tọa độ điểm D là chân đường  phân giác trong kẻ từ đỉnh B của tam giác ABC.

Câu 2: Trong không gian Oxyz cho ba điểm A(1, 2,-1), B(2,-1,3), C(4,-7,5) tạo thành tam giác. Tìm tọa độ điểm D là chân đường phân giác trong kẻ từ đỉnh B của tam  giác ABC.

[button size=”medium” style=”primary” text=”TẢI BỘ ĐỀ THI” link=”https://drive.google.com/drive/folders/1tkCX1kEwDeiQMNpK9xqu9AfIHLUMAlLa?usp=sharing” target=””]

Phương pháp toạ độ hoá hình học không gian

Đôi khi trong giải toán hình học không gian cổ điển ta sẽ gặp khá nhiều bài toán tính toán phức tạp, tuy nhiên trong phòng thi ta lại không có nhiều thời gian, vì thế trong chương này chúng ta sẽ tìm hiểu một phương pháp giải quyết nhanh các bài toán tính toán phức tạp và khó trong hình không gian cổ điển, liên quan tới cực trị, góc, khoảng cách.

Phương pháp: Trên mạng có một vài tài liệu nói về phương pháp này và chia thành rất nhiều dạng, điều đó làm chúng ta khi áp dụng có phần khó nhớ và máy móc, tuy nhiên chúng ta chỉ cần nắm được dấu hiệu và phương pháp sau:

• Bước 1. Chọn hệ trục tọa độ. Trong bước này ta sẽ xác định 3 đường vuông góc có trong bài toán và gọi đó là 3 đường cơ sở. Thông thường thì ta sẽ quy ước trục Ox hướng vào mình, trục Oz nằm ngang, còn lại là trục Oy.
• Bước 2. Xác định tọa độ các điểm liên trên hình liên quan tới bài toán. Với những bạn chưa quen thì chúng ta xác định tọa độ hình chiếu của điểm cần tìm lên các trục, từ đó sẽ suy ra được tọa độ điểm cần tính.
• Bước 3. Áp dụng công thức.

Một số công thức cần nhớ trong phần này:

• Diện tích và thể tích: Diện tích tam giác, Thể tích tứ diện, Thể tích hình hộp, Thể tích hình lăng trụ.
• Góc: Góc giữa 2 mặt phẳng, Góc giữa 2 đường thẳng, Góc giữa đường thẳng và mặt phẳng.
• Khoảng cách:  Khoảng cách từ điểm đến mặt phẳng, Khoảng cách từ một điểm đến 1 đường thẳng, Khoảng cách giữa hai đường thẳng chéo nhau.

Chú ý: Thông thường các bài mà không có 3 đường vuông góc thì ta sẽ phải tự dựng thêm để gắn tọa độ và những bài liên quan tới hình lập phương, hình hộp chữ nhật, khối chóp có 3 đường vuông góc, lăng trụ đứng thì khi áp dụng phương pháp này sẽ giải rất nhanh.

[button size=”medium” style=”primary” text=”BÀI TẬP MINH HOẠ” link=”https://drive.google.com/drive/folders/1tkCX1kEwDeiQMNpK9xqu9AfIHLUMAlLa?usp=sharing” target=””]

Xem thêm:

• Bộ đề thi tham khảo tuyển sinh cấp 3 môn tiếng anh
• 4 bộ đề thi tham khảo tuyển sinh cấp 3 môn văn
• Tổng hợp công thức 12 thì, cách dùng và dấu hiệu nhận biết các thì Tiếng Anh

Trên đây là đề cương ôn tập thi học kì 2 lớp 12 môn toán. Gồm các dạng toán ôn tập, lượng bài tập phong phú, đa dạng. Trọn bộ đề thi thử học kì 2 môn Toán lớp 12 và các bài toán trong đề thi tốt nghiệp THPT những năm gần đây. Chúc các em học tập thật tốt!