Các công thức đạo hàm, nguyên hàm là phần kiến thức Toán 11 rất quan trọng và có phần hơi khó khăn đối với nhiều người. Với mục đích chia sẻ tất cả kiến thức từ cơ bản đến nâng cao cho mọi người có thể dễ dàng ôn tập một cách đơn giản và nhanh chóng.
Hôm nay Bamboo xin gửi đến các bạn đầy đủ và chi tiết tất cả kiến thức về bảng công thức đạo hàm cùng các kiến thức cần ghi nhớ. Các bạn xem xong đừng quên lưu lại nhé!
Đạo hàm là gì? Quy tắc cơ bản của đạo hàm
Định nghĩa đạo hàm, đạo hàm sơ cấp, đạo hàm cao cấp
Trong giải tích toán học, đạo hàm của một hàm số là một đại lượng mô tả sự biến thiên của hàm tại một điểm nào đó. Đạo hàm là một khái niệm cơ bản trong giải tích (Theo Wikipedia).

Quy tắc cơ bản của đạo hàm

Nguyên hàm là gì? Định lí, tính chất của nguyên hàm
Trong bộ môn giải tích, một nguyên hàm của một hàm số thực cho trước f là một hàm F có đạo hàm bằng f, nghĩa là, F′ = f. Quá trình tìm nguyên hàm được gọi là tích phân bất định. (Theo Wikipedia)

Định lý nguyên hàm
Định lý 1: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x)=F(x)+CG(x)=F(x)+C cũng là một nguyên hàm của hàm số f(x) trên K.
Định lý 2: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x)+CF(x)+C với C là một hằng số tùy ý.
Định lí 3: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)′=f(x)(∫f(x)dx)′=f(x) và ∫f′(x)dx=f(x)+C∫f′(x)dx=f(x)+C
Tính chất 2: ∫kf(x)dx=k∫f(x)dx∫kf(x)dx=k∫f(x)dx với K là hằng số khác 0.
Tính chất 3: ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx
Bảng công thức đạo hàm – đạo hàm lượng giác

Công thức đạo hàm cơ bản
- Đạo hàm của f(x) với x là biến số
- Đạo hàm của f(u) với u là hàm số
- Đạo hàm của một số phân thức hữu tỉ thường gặp

Công thức đạo hàm các hàm số sơ cấp

Đạo hàm cấp cao

Đạo hàm của một số phân thức hữu tỉ thường gặp

Bảng đạo hàm của các hàm lượng giác và các hàm lượng giác ngược
+ Đạo hàm của các hàm lượng giác là phương pháp toán học tìm tốc độ biến thiên của một hàm số lượng giác theo sự biến thiên của biến số. Các hàm số lượng giác thường gặp là sin(x), cos(x) và tan(x).
+ Biết được đạo hàm của sin(x) và cos(x), chúng ta dễ dàng tìm được đạo hàm của các hàm lượng giác còn lại do chúng được biểu diễn bằng hai hàm trên, bằng cách dùng quy tắc thương.
+ Phép chứng minh đạo hàm của sin(x) và cos(x) được diễn giải ở bên dưới, và từ đó cho phép tính đạo hàm của các hàm lượng giác khác.
+ Việc tính đạo hàm của hàm lượng giác ngược và một số hàm lượng giác thông dụng khác cũng được trình bày ở bên dưới.
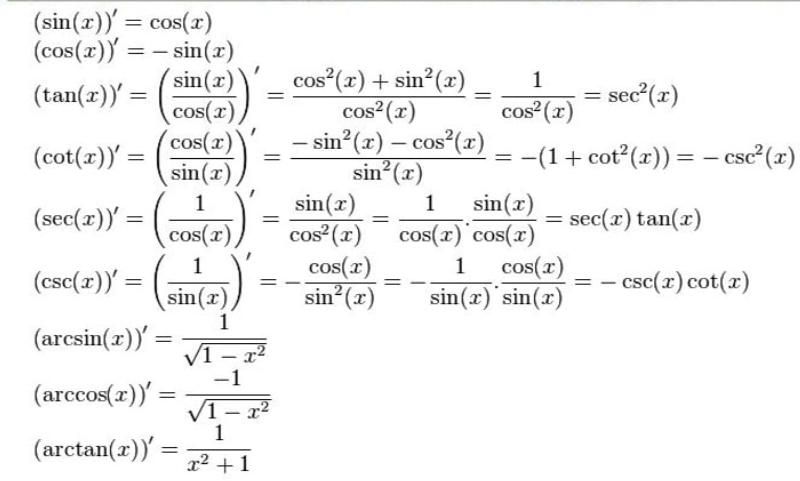
Bảng công thức nguyên hàm – nguyên hàm lượng giác
Gồm các công thức nguyên hàm cơ bản, nguyên hàm nâng cao dành cho các học sinh lớp 12 áp dụng để làm các bài tập về nguyên hàm
Bảng các nguyên hàm cơ bản thường gặp
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
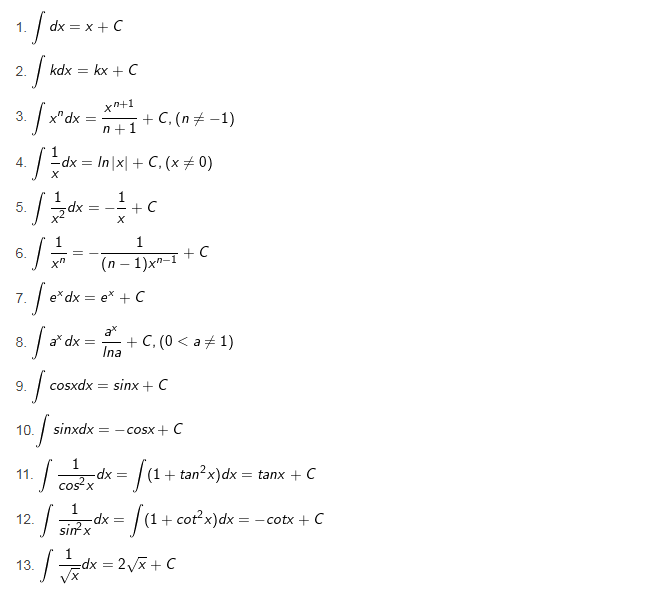
Bảng các nguyên hàm mở rộng (a ≠ 0)

Bảng các nguyên hàm nâng cao (a ≠ 0)
Bảng công thức nguyên hàm là vô cùng quan trọng và không thể thiếu đối với các bạn học sinh lớp 12 với phần học giải tích.

Một số dạng bài tập cách tính nguyên hàm các dạng thường gặp
Dạng 1.1 Hàm đa thức
- Phương pháp giải
Để tính nguyên hàm của các hàm đa thức ta cần sử dụng các công thức sau:
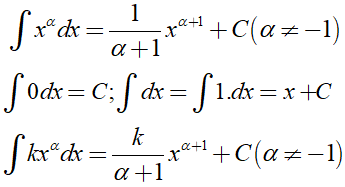
Trong đó, k là hằng số.
![]()
- Ví dụ minh họa
Ví dụ 1. Họ nguyên hàm của hàm số f(x)= x2 − 2x + x−2 là
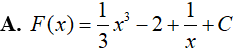

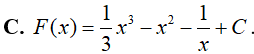
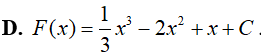
Đáp án: C
![]()
![]()
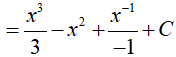
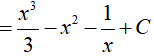
Ví dụ 2. Trong các hàm số sau đây, hàm số nào là một nguyên hàm của hàm số:
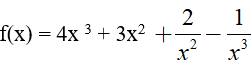
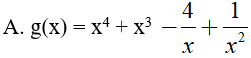
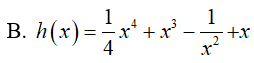
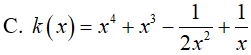
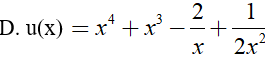
Đáp án: D
Ta có:

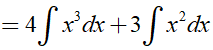
![]()
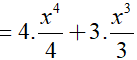
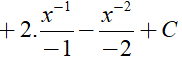
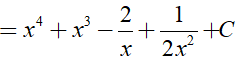
Dạng 1.2. Hàm phân thức
- Phương pháp giải
Để tìm nguyên hàm của các hàm phân thức ta cần sử dụng các công thức sau:
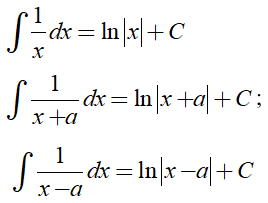
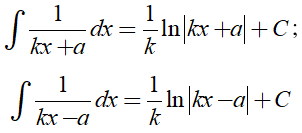
2. Ví dụ minh họa
Ví dụ 1. Cho 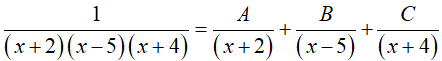
đó tổng S = A + B + C bằng


Đáp án: B
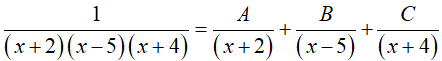
=> A(x − 5)(x + 4) + B(x + 2)(x + 4) + C(x + 2)(x − 5) = 1
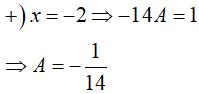
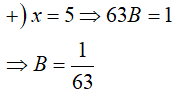
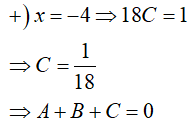
Ví dụ 2. Tìm 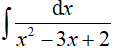 là:
là:
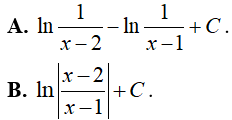
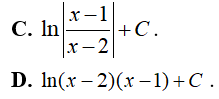
Đáp án: B
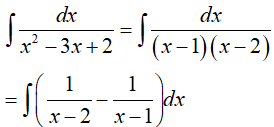
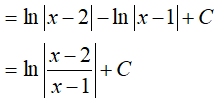
Dạng 1.3: Hàm chứa căn thức
- Phương pháp giải
Để tìm nguyên hàm của các hàm chứa căn thức ta cần linh hoạt sử dụng các công thức sau:
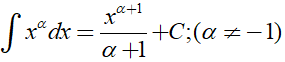
![]()
2. Ví dụ minh họa
Ví dụ 1. Tìm nguyên hàm của hàm số 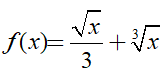
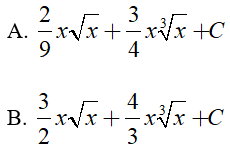
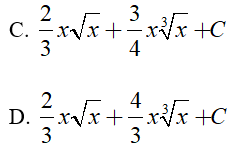
Đáp án: A
Ta có:
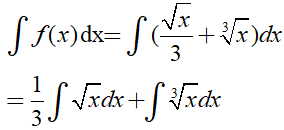
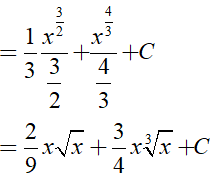
Ví dụ 2. Tìm 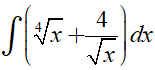
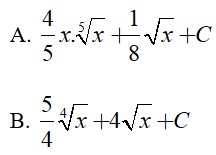
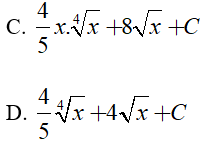
Đáp án C
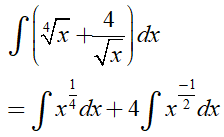
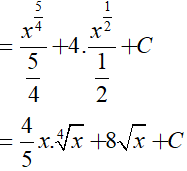
Dạng 1.4: Hàm lượng giác
- Phương pháp giải
Để tìm nguyên hàm của hàm số lượng giác ta cần sử dụng các công thức sau:
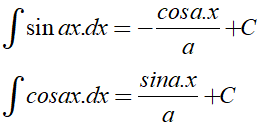
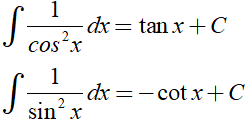
Ngoài ra, ta cần sử dụng các tính chất của nguyên hàm; các công thức cộng, công thức nhân đôi, công thức biến đổi tích thành tổng, công thức hạ bậc…
2. Ví dụ minh họa
Ví dụ 1. Nguyên hàm của hàm số f(x) = 4cos4x là
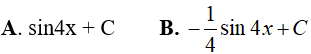
![]()
Đáp án: A
Ta có:
![]()
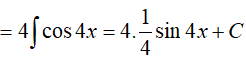
![]()
Ví dụ 2. Tính ![]() , kết quả là:
, kết quả là:
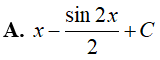
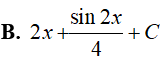

![]()
Đáp án: C
Ta có:
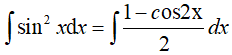
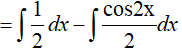
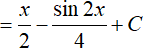
Một số dạng bài tập cách tính đạo hàm các dạng thường gặp
Dạng 1: Tính đạo hàm của hàm số
Bài 1: Tìm đạo hàm của các hàm số sau:
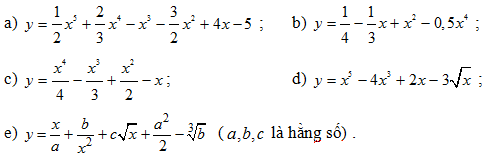
Đáp số:
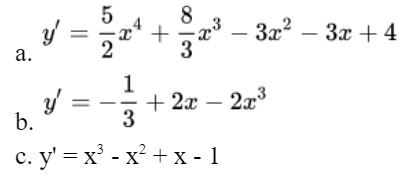
Bài 2: Tìm đạo hàm của các hàm số sau:
Đáp số
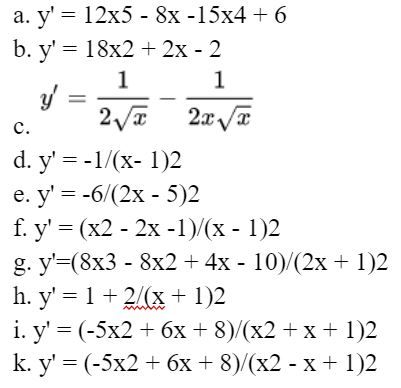
Dạng 2: Giải phương trình y’ = 0
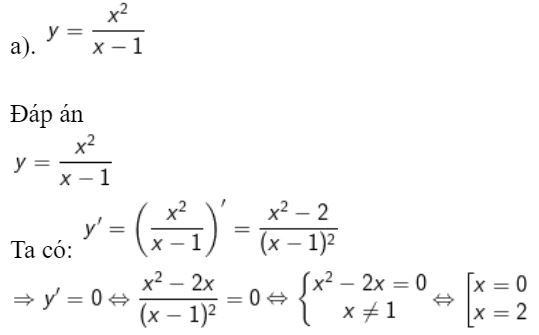
Ta thấy 2 nghiệm đều thỏa điều kiện x khác 1 nên phương trình y’=0 có 2 nghiệm phân biệt là x=0 và x=2
Dạng 3: Chứng minh đẳng thức về đạo hàm
Phương pháp: Tính đạo hàm và sử dụng các phép biến đổi về lượng giác
Ví dụ 1: Chứng minh rằng

Xem thêm:
R trong toán học là gì? Định nghĩa, tính chất và bài tập minh họa có giải
Tổng hợp các công thức lượng giác lớp 9, 10, 11 đầy đủ nhất
Các tính tỉ số phần trăm và các dạng toán về tỉ số phần trăm cơ bản có đáp án
Bên trên là một số thông tin cơ bản về đạo hàm, nguyên hàm bạn cần biết. Mọi thắc mắc về bảng đạo hàm, nguyên hàm, công thức tính nguyên hàm từ cơ bản đến nâng cao mong sẽ giúp được chút kiến thức cho các bạn.











