Chắc hẳn công thức lượng giác đã không còn quá xa lạ với các em học sinh cấp 2 và cấp 3. Đây được xem là điểm quan trọng và cốt lõi cho hầu hết các bài toán hình học về lượng giác – phần kiến thức luôn xuất hiện trong các đề thi học kỳ lẫn THPTQG. Để “mang điểm cao về cho mẹ”, không còn cách nào ngoài việc nắm thật vững và vận dụng “trơn tru” các công thức để giải bài tập.
Sau đây là cách mà Bamboo gợi ý để bạn không còn “rối não” khi làm bài tập về lượng giác:
- Ôn thật kỹ các phần cơ bản trong lý thuyết về lượng giác và các hàm lượng giác.
- Bỏ túi các công thức lượng giác và mẹo ghi nhớ mà Bamboo sắp giới thiệu sau đây.
- Áp dụng công thức vào đa dạng bài tập và luyện tập thường xuyên.
Nếu bạn đang gặp khó khăn trong việc hệ thống lại và ghi nhớ nhanh toàn bộ công thức lượng giác lớp 9, 10, 11 từ cơ bản đến nâng cao, hãy để Bamboo giúp bạn qua bài viết bên dưới nhé!
Công thức lượng giác là gì?
Công thức lượng giác được các bạn học sinh nhớ đến như cái tên thân thuộc của các đẳng thức lượng giác, gồm nhiều phương trình chứa các hàm lượng giác. Các đẳng thức này sẽ làm đơn giản hoá các biểu thức lượng giác và các bài toán tính tích phân trong chương trình toán cấp 3 nếu được áp dụng một cách hợp lý.

Bảng giá trị lượng giác của một số cung hay góc đặc biệt
Dấu của hàm số lượng giác của một số góc bất kỳ
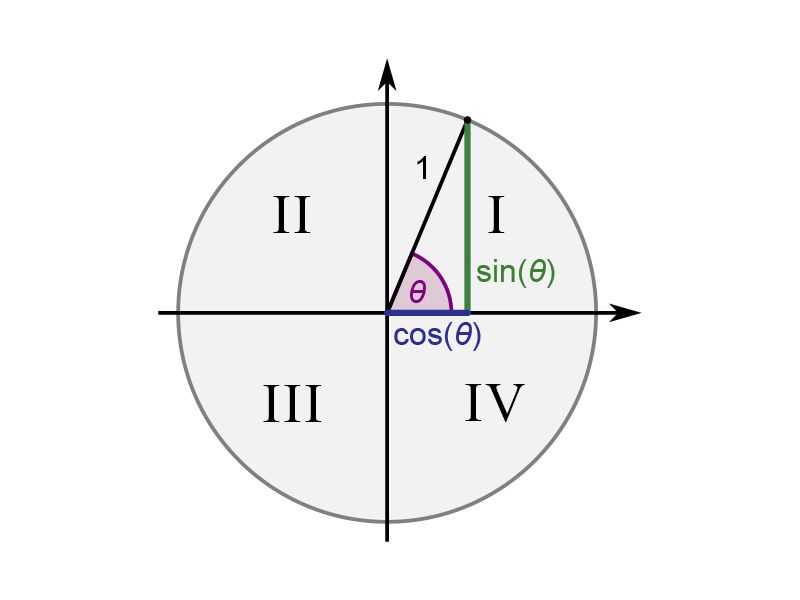
Dấu hàm lượng giác trong đường tròn lượng giác
[wptb id=5714]
Giá trị hàm số của góc α > 0
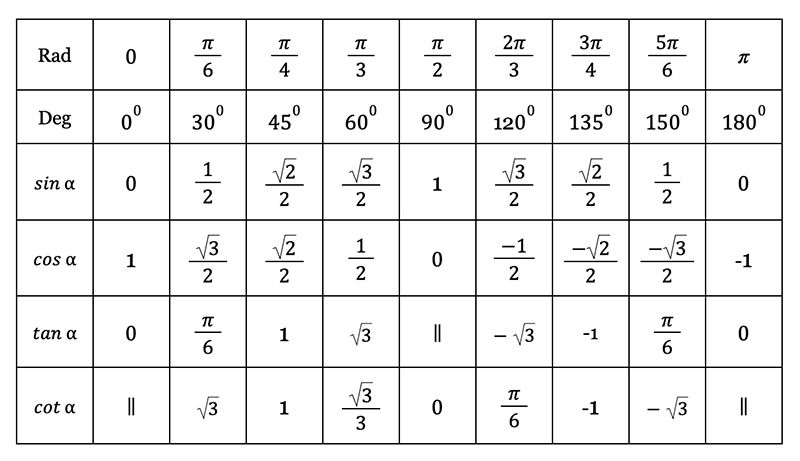
Bảng giá trị lượng giác với góc đặc biệt lớn hơn 0
Giá trị hàm số của góc α > 0
Giá trị tuyệt đối của bảng giá trị lượng giác được giữ nguyên nhưng có sự thay đổi về dấu. Dựa vào đường tròn lượng giác, mối liên hệ của các hàm với nhau để xác định dấu của giá trị lượng giác với các góc bé hơn 0.
Tổng hợp công thức lượng giác lớp 9,10,11 đầy đủ nhất
Công thức lượng giác cơ bản
- Cung liên kết
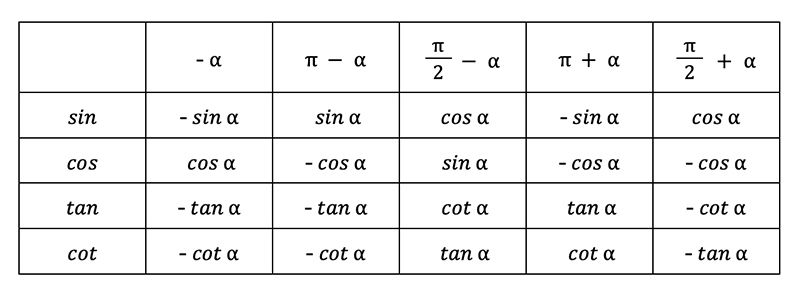
Công thức lượng giác của các cung liên kết
Mẹo ghi nhớ: Cos đối, sin bù, phụ chéo, tan cot hơn π, sin chéo π/2
- Hệ thức cơ bản
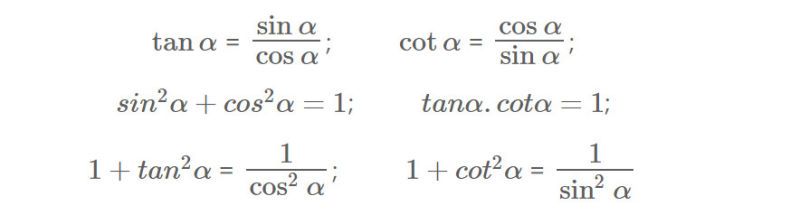
Công thức cộng
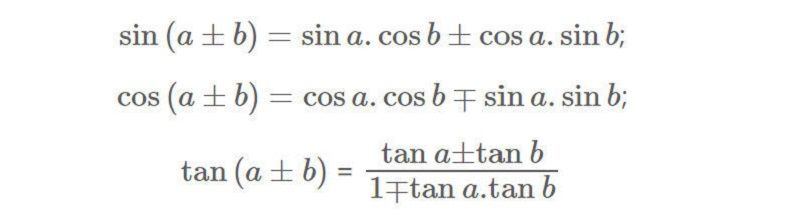
Mẹo ghi nhớ:
Sin thì sin cos cos sin
Cos thì cos cos sin sin “coi chừng” (dấu trừ)
Tang tổng thì lấy tổng tang
Chia một trừ với tích tang.
Công thức nhân (công thức góc bội)
- Nhân đôi
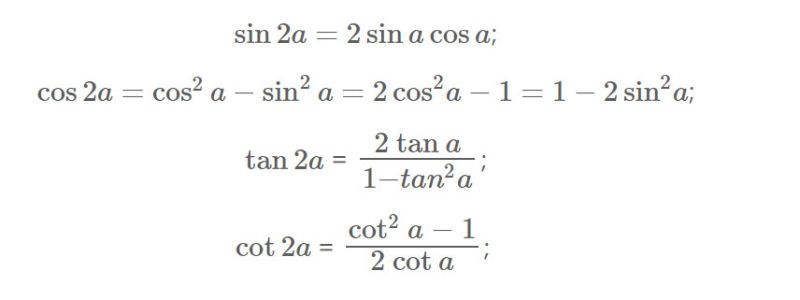
Mẹo ghi nhớ:
Sin gấp đôi = 2 sin cos
Cos gấp đôi = bình cos trừ bình sin
= trừ 1 + 2 lần bình cos
= + 1 trừ 2 lần bình sin
Tang đôi ta lấy đôi tang (2 tang), chia 1 trừ lại bình tang, ra liền.
- Nhân ba
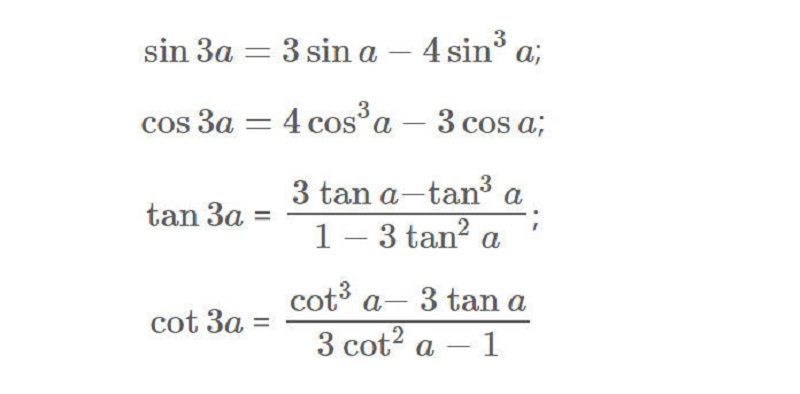
Mẹo ghi nhớ:
Nhân ba một góc bất kỳ,
Sin thì ba bốn, cos thì bốn ba,
Dấu trừ đặt giữa 2 ta, lập phương chỗ bốn, thế là ok.
- Nhân bội
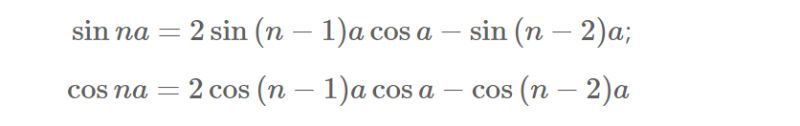
Công thức hạ bậc
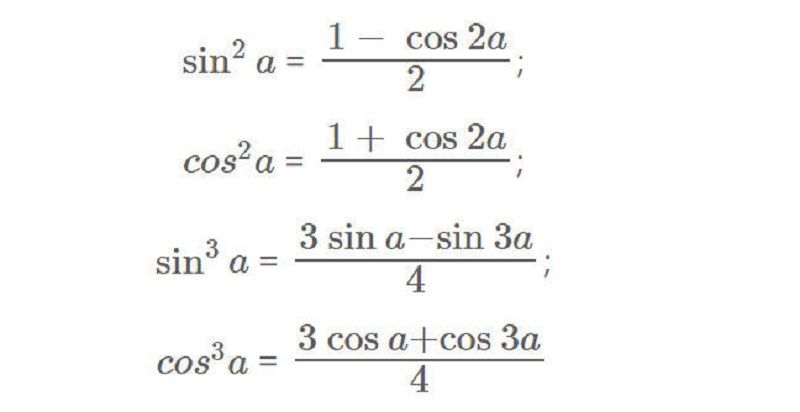
Công thức biến đổi tích thành tổng, hiệu
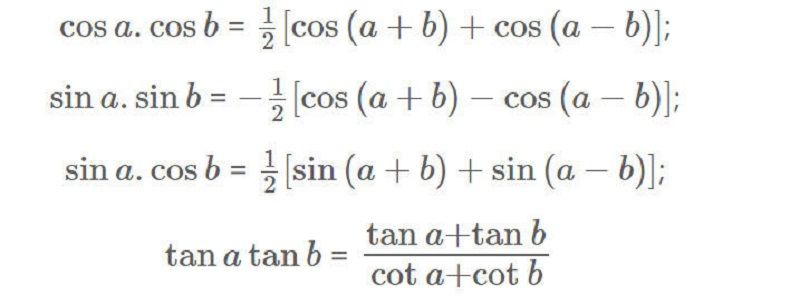
Mẹo ghi nhớ:
Cos cos nửa cos cos
Sin sin trừ nửa cos cos
Sin cos nửa sin sin.
Công thức biến đổi tổng, hiệu thành tích
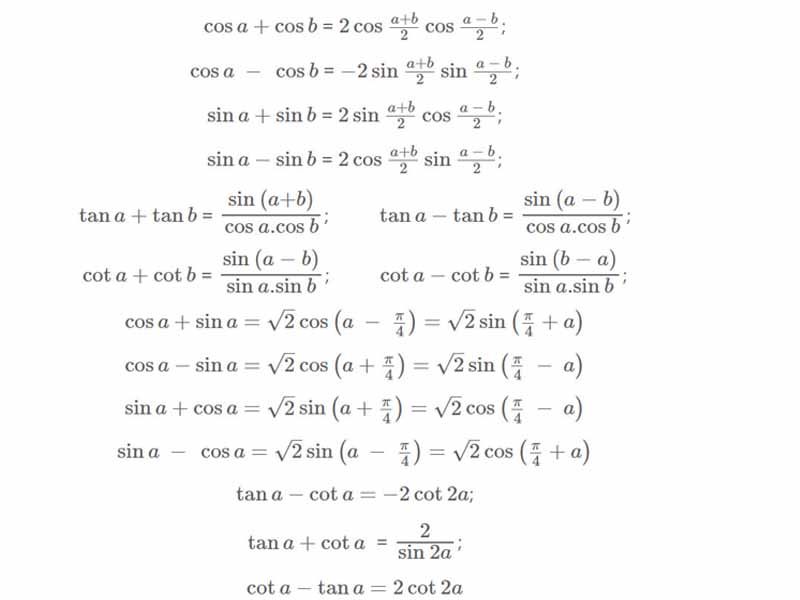
Mẹo ghi nhớ:
Cos cộng cos bằng 2 cos cos
Cos trừ cos bằng -2 sin sin
Sin cộng sin bằng 2 sin cos
Sin trừ sin bằng 2 cos sin
Tan a + tan b: tình mình cộng lại tình ta, sinh ra 2 đứa con mình con ta
Tan a – tan b: tình mình hiệu với tình ta sinh ra hiệu chúng, con ta con mình.
Công thức biểu diễn theo tan
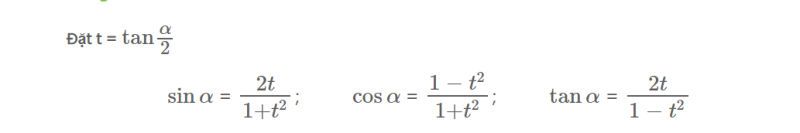
Công thức nghiệm của phương trình lượng giác cơ bản
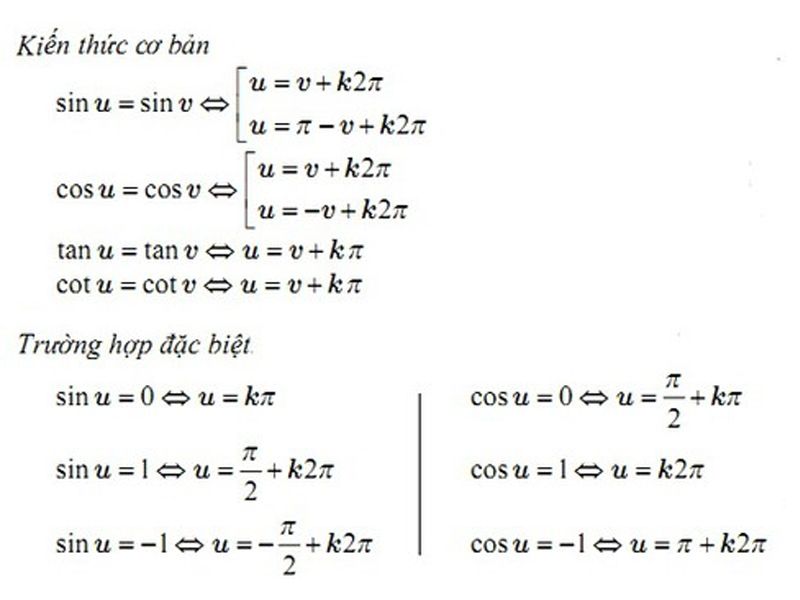
Công thức nghiệm của phương trình lượng giác
Tải bảng công thức lượng giác đầy đủ nhất
[button size=”medium” style=”secondary” text=”TẢI NGAY BẢNG CÔNG THỨC LƯỢNG GIÁC” link=”https://drive.google.com/file/d/12-c-bPgW3QN0zFv_2B5GzwT8gQbJ7DlN/view?usp=sharing” target=””]
Xem thêm:
- Công thức tính diện tích tam giác, hình thoi, hình vuông, hình chữ nhật, hình tròn
- Công thức tính chu vi hình vuông, chữ nhật, tam giác, hình tròn, hình thoi
- Tổng hợp đề thi tin học trẻ tiểu học, THCS, THPT có đáp án
Và đó là toàn bộ tâm huyết của Bamboo dành cho các bạn học sinh đang còn “hoang mang” với lượng giác, hy vọng bài tổng hợp các công thức lượng giác sẽ giúp bạn có thể ôn luyện cũng như ghi nhớ các công thức lượng giác dễ dàng hơn. Đừng quên theo dõi tin tức của Bamboo để cập nhật nhiều kiến thức bổ ích khác nữa nhé!









