Tính bằng cách thuận tiện nhất được xem là phương pháp tính nhanh và hiệu quả cho các bài toán tiểu học từ cơ bản đến nâng cao, trải dài từ lớp 1 đến lớp 5. Nắm được phương pháp này, không những các em học sinh sẽ nhanh chóng đưa ra đáp án đúng một cách hợp lý, mà còn rèn luyện được tư duy nhạy bén với con số – vốn là nỗi sợ của phần lớn các em. Còn chần chờ gì nữa, hãy cùng Bamboo School khám phá về 5 mẹo tính thuận tiện và bài tập minh hoạ có lời giải ở bên dưới nhé!
Tính bằng cách thuận tiện nhất là gì?

Tính bằng cách thuận tiện nhất là việc áp dụng các tính chất của phép cộng, phép nhân,… vào việc giải bài toán tính giá trị của biểu thức một cách nhanh, hợp lí và chính xác nhất.
Cách tính và mẹo tính bằng cách thuận tiện nhất
Quy tắc 1: Nhóm/tách các số trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn, hoặc để xuất hiện nhân số chung
Quy tắc 2: Phép cộng các số giống nhau được biểu diễn bằng phép nhân
Quy tắc 3: Vận dụng các tính chất của phép cộng, phép nhân, phép trừ, phép chia
- Nhân một số với một tổng: a x (b + c) = a x b + a x c
- Nhân một số với một hiệu: a x (b – c) = a x b – a x c
- Một tổng chia cho một số: (a + b) : c = a : c + b : c
- Một số trừ đi một tổng: a – (b + c) = a – b – c
Quy tắc 4: Vận dụng các tính chất với các số đặc biệt
- 0 nhân với một số: 0 x a = a x 0 = 0
- 0 chia cho một số: 0 : a = 0
- 1 nhân với một số: 1 x a = a x 1 = a
- Chia một số cho 1: a : 1 = a
Quy tắc 5: Tính thuận tiện với biểu thức có phân số
Kết hợp các thao tác sau:
- Nhóm các phân số trong biểu thức thành từng nhóm có tổng (hoặc hiệu) bằng 1 hoặc 0.
- Vận dụng tính chất của 4 phép tính để tách, ghép ở tử số hoặc ở mẫu số nhằm tạo ra thừa số giống nhau ở cả mẫu số và tử số rồi thực hiện rút gọn biểu thức.
- Phép cộng các số giống nhau được biểu diễn bằng phép nhân
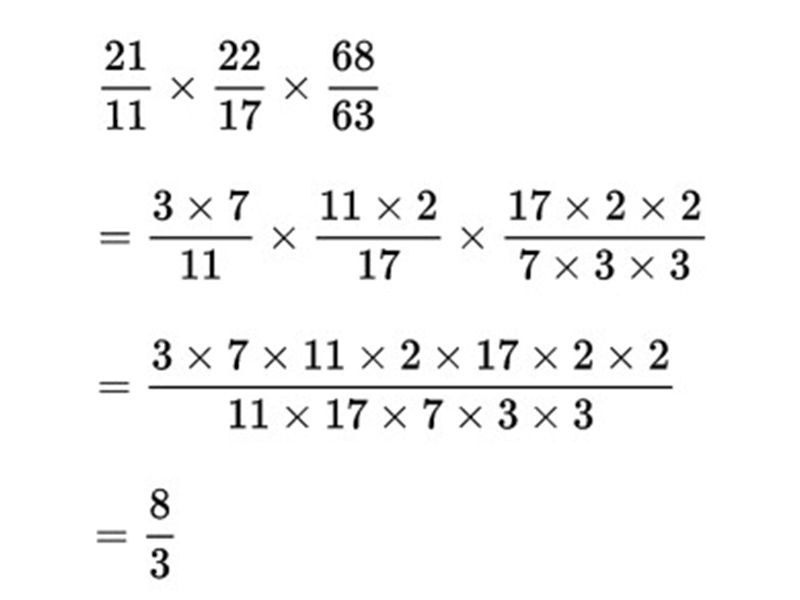
Ví dụ tính bằng cách thuận tiện nhất với phân số
Một số dạng bài tập tính bằng cách thuận tiện nhất
Tính bằng cách thuận tiện nhất 0,12 x 400
Lời giải tham khảo:
0,12 x 400
= 0,12 x 100 x 4 (Áp dụng quy tắc 1: Tách 400 thành tích có số tròn trăm)
= 12 x 4
= 48
Tính bằng cách thuận tiện nhất 142 x 12 + 142 x 18
Lời giải tham khảo:
142 x 12 + 142 x 18
= 142 x (12 + 18) (Áp dụng tính chất nhân một số với một tổng)
= 142 x 30
= 4260
Tính bằng cách thuận tiện nhất 49 x 365 – 39 x 365
Lời giải tham khảo:
49 x 365 – 39 x 365
= 365 x (49 – 39) (Áp dụng tính chất nhân một số với một tổng)
= 365 x 10
= 3650
Tính bằng cách thuận tiện nhất 43 x 95 + 5 x 43
Lời giải tham khảo:
43 x 95 + 5 x 43
= 43 x (95 + 5) (Áp dụng tính chất nhân một số với một tổng)
= 43 x 100
= 4300
Tính bằng cách thuận tiện nhất 125 x 12 + 12 x 874 + 12
Lời giải tham khảo:
125 x 12 + 12 x 874 + 12
= 12 + (125 + 874 + 1) (Áp dụng tính chất nhân một số với một tổng)
= 12 x 1000
= 12000
Tính bằng cách thuận tiện nhất 46 x 17 + 38 x 46 + 26 x 44 + 46
Lời giải tham khảo:
46 x 17 + 38 x 46 + 26 x 44 + 46
= 46 x (17 + 38 + 1) + 26 x 44 (Áp dụng tính chất nhân một số với một tổng)
= 46 x 56 + 26 x 44
= 46 x (100 – 44) + (46 – 20) x 44 (Áp dụng quy tắc 1: Tách 56 thành hiệu có số tròn trăm, tách 26 thành hiệu để xuất hiện thừa số chung)
= 46 x 100 – 46 x 44 + 46 x 44 – 20 x 44 (Hai phép tính triệt tiêu nhau)
= 46 x 100 – 20 x 44
= 4600 – 880
= 3720
Xem thêm:
- Công thức tính chu vi hình vuông, chữ nhật, tam giác, hình tròn, hình thoi
- Công thức tính diện tích tam giác, hình thoi, hình vuông, hình chữ nhật, hình tròn
- Những mẫu thơ về cô giáo tiểu học ngắn, dài ,hay, ý nghĩa
Ngoài 6 lời giải tham khảo phía trên, các em học sinh có thể tự sưu tầm bài tập và sáng tạo ra nhiều cách giải khác nhau để luyện tập nhuần nhuyễn hơn. Bamboo hy vọng bài viết này sẽ giúp các em dễ dàng hiểu được kiến thức cơ bản về phương pháp tính bằng cách thuận tiện nhất và áp dụng chúng để chinh phục các bài toán biểu thức “khó nhằn”.









