Công thức, cách đọc và mẹo học thuộc 7 hằng đẳng thức đáng nhớ

Làm thế nào để học thuộc và vận dụng tốt hằng đẳng thức đáng nhớ vào các dạng Toán chắc hẳn cũng là câu hỏi chung của nhiều bạn học sinh. Việc học Toán sẽ trở nên đơn giản hơn rất nhiều nếu bạn nắm vững lý thuyết và kiến thức nền tảng. Hãy cùng Bamboo School tìm hiểu rõ hơn về 7 hằng đẳng thức đáng nhớ – THCS và làm quen với một số dạng bài tập thường gặp nhé!

Khái niệm về hằng đẳng thức đáng nhớ

Các hằng đẳng thức đáng nhớ chính là các đẳng thức cơ bản nhất, được áp dụng trong các phép tính cộng, trừ, nhân và chia đa thức với đa thức. Về cơ bản, những hằng đẳng thức này đã được khai triển, chứng minh, sau đó được rút ra thành công thức chung để áp dụng trong mọi trường hợp.

Việc vận dụng hằng đẳng thức đáng nhớ để giải Toán sẽ giúp người học tiết kiệm thời gian hơn trong việc biến đổi, phân tích đa thức thành nhân tử hoặc ngược lại, làm các dạng Toán liên quan đến phép chứng minh. Ở lớp 8 thuộc bậc Trung học cơ sở, học sinh sẽ được thầy cô giảng dạy về 7 hằng đẳng thức đáng nhớ lớp 8, đi từ đơn giản đến phức tạp, có liên quan đến bình phương và lập phương.

Hằng đẳng thức đáng nhớ được áp dụng để tính cộng, trừ, nhân, chia đa thức với đa thức

7 hằng đẳng thức đáng nhớ

Dưới đây là 7 hằng đẳng thức đáng nhớ lớp 8 được áp dụng trong nhiều dạng Toán khác nhau. Mời các bạn cùng tìm hiểu.

Bình phương của một tổng

– Công thức: (A + B)² = A² + 2AB + B²

– Cách đọc: Bình phương của một tổng hai số A và B bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất và số thứ hai, rồi cộng với bình phương của số thứ hai
– Ví dụ: 

• (x + 5)² = x² + 10x + 25
• (y + 7)² = y² + 14y + 49

Công thức bình phương của một tổng

Bình phương của một hiệu

– Công thức: (A – B)² = A² – 2AB + B²
– Cách đọc: Bình phương của một hiệu hai số A và B bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, rồi cộng với bình phương của số thứ hai
– Ví dụ: 

• (3 – x)² = 9 – 6x + x²
• (2x – 5y)² = 4x² – 20xy + 25y²

Bình phương của một hiệu

Hiệu hai bình phương

– Công thức: A² – B² = (A – B)(A + B)

– Cách đọc: Hiệu hai bình phương của hai số A và B bằng hiệu của hai số đó nhân với tổng của hai số đó

– Ví dụ:

• 9x² – 25y² = (3x – 5y)(3x + 5y)
• 16y² – x²/4 = (4y – x/2)(4y + x/2)

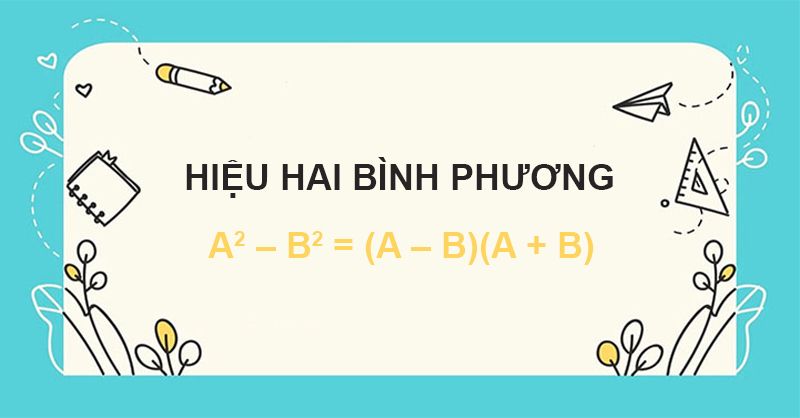
Công thức hiệu hai bình phương

Lập phương của một tổng

– Công thức: (A + B)³ = A³ + 3A²B + 3AB² + B³
– Cách đọc: Lập phương của một tổng của hai số A và B bằng lập phương của số thứ nhất cộng với ba lần tích của bình phương số thứ nhất nhân với số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương số thứ hai, rồi cộng với lập phương của số thứ hai

– Ví dụ:

• (x + 4)³ = x³ + 12x² + 48x + 64
• (y + 2)³ = y3 + 6y² + 12y + 8

Lập phương của một tổng

Lập phương của một hiệu

– Công thức: (A – B)³ = A³ – 3A²B +3AB² – B³
– Cách đọc: Lập phương của một hiệu của hai số A và B bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân với số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương số thứ hai, rồi trừ đi lập phương của số thứ hai

– Ví dụ:

• (x – 4)³ = x³ – 12x² + 48x – 64
• (y + 2)³ = y3 – 6y² + 12y – 8

Lập phương của một hiệu

Tổng hai lập phương

– Công thức: A³ + B³ = (A + B)(A² – AB + B²)

– Cách đọc: Tổng hai lập phương của hai số A và B bằng tổng của số thứ nhất cộng với số thứ hai, nhân với bình phương thiếu hiệu của số thứ nhất trừ đi số thứ hai
– Ví dụ:

• x³ + 8y³ = (x + 2y)(x² – 2xy + 4y²)
• 27 + a³ = (3 + a)(9 – 3a + a²)

Tổng hai lập phương

Hiệu hai lập phương

– Công thức: A³ – B³ = ( A – B)(A² + AB + B²)
– Cách đọc: Hiệu hai lập phương của hai số A và B bằng hiệu của số thứ nhất trừ đi số thứ hai, nhân với bình phương thiếu tổng của số thứ nhất và số thứ hai

– Ví dụ:

• x³ – 8y³ = (x – 2y)(x² + 2xy + 4y²)
• 27 – a³ = (3 – a)(9 + 3a + a²)

Hiệu hai lập phương

Bài tập tự luyện về hằng đẳng thức có đáp án

Sau đây là một số dạng bài tập vận dụng 7 hằng đẳng thức đáng nhớ lớp 8 cơ bản. Mời các bạn cùng tham khảo.

• Bài tập 1: Công thức nào sau đây tương ứng với hằng đẳng thức hiệu hai lập phương?

A. A³ – B³ = ( A – B)(A² – AB + B²)

B. A³ – B³ = ( A – B)(A² + AB + B²)

C. A³ + B³ = (A + B)(A² – AB + B²)

D. A³ + B³ = (A + B)(A² + AB + B²)

Đáp án: B

• Bài tập 2: Hãy viết lại các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a. x² + 4x + 1

b. 16x² – 24x + 9

Đáp án:

a. x² + 4x + 1 = x² + 2.2x.1 + 1² = (x + 1)²

b. 16x² – 24x + 9 = (4x)² – 2.4x.3 + 3² = (4x – 3)²

• Bài tập 3: Phát biểu nào dưới đây là sai?

A. Lập phương của một hiệu của hai số A và B bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân với số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương số thứ hai, rồi trừ đi lập phương của số thứ hai

B. Hiệu hai lập phương của hai số A và B bằng hiệu của số thứ nhất trừ đi số thứ hai, nhân với bình phương thiếu hiệu của số thứ nhất trừ đi số thứ hai

C. Bình phương của một tổng hai số A và B bằng bình phương của số thứ nhất cộng với hai lần tích của số thứ nhất và số thứ hai, rồi cộng với bình phương của số thứ hai

D. Hiệu hai bình phương của hai số A và B bằng hiệu của hai số đó nhân với tổng của hai số đó

Đáp án: B

• Bài tập 4: Tính 5³– 3³

Đáp án: 5³– 3³ = (5 – 3)(5² + 5.3 + 3²) = 2.49 = 98

• Bài tập 5: Hãy viết lại đa thức sau đây dưới dạng hiệu hai lập phương: (x – 2y)(x² + 2xy + 4y²)

Đáp án: (x – 2y)(x² + 2xy + 4y²) = x³ – (2y)³ = x³ – 8y³

• Bài tập 6: Tìm x, biết:

a. (x – 3)(x²+ 3x + 9) + x(x + 2)(2 – x) = 0

b. (x + 1)³– (x – 1)³– 6(x – 1)² = – 10

Đáp án:

a. Ta có: (x – 3)(x²+ 3x + 9) + x(x + 2)(2 – x) = 0

⇔ x³ – 3³ + x(2² – x²) = 0

⇔ x³ – x³ + 4x – 27 = 0

⇔ 4x – 27 = 0

⇔ x = 27/4

b. Ta có: (x + 1)³– (x – 1)³– 6(x – 1)² = – 10

⇔ (x³ + 3x² + 3x + 1) – ( x³ – 3x² + 3x – 1) – 6(x² – 2x + 1) = – 10

⇔ 6x² + 2 – 6x² + 12x – 6 = – 10

⇔ 12x – 4 = – 10

⇔ 12x = – 6

⇔ x = –1/2

Xem thêm:

• 7 cách viết ký hiệu toán học trong word đơn giản nhanh chóng
• 10 cách học giỏi toán hiệu quả nhất cho người mất gốc
• R trong toán học là gì? Định nghĩa, tính chất và bài tập minh họa có giải

Hy vọng qua bài viết trên, các bạn đã phần nào nắm được công thức, cũng như làm quen với một số dạng bài tập cơ bản áp dụng 7 hằng đẳng thức đáng nhớ. Chúc các bạn sẽ luôn gặt hái kết quả cao trong tất cả các môn học.