Vectơ là gì? Các định nghĩa và bài tập minh hoạ về vectơ

Trong Toán học, hẳn các bạn đã từng nghe đến khái niệm vectơ. Vậy cụ thể thì vectơ là gì? Có những loại vectơ nào và cách nhận diện từng loại cụ thể? Dưới đây là tổng hợp những kiến thức về Trung học Phổ thông, ví dụ minh họa và một số bài tập về các dạng vectơ thường gặp nhất trong các dạng đề thi. Hãy cùng Bamboo School tìm hiểu nhé!

Vectơ là gì?

Vectơ được định nghĩa là một đoạn thẳng có hướng. Tức là trong hai điểm mút của đoạn thẳng có chỉ rõ điểm nào là điểm đầu và điểm nào là điểm cuối. Vectơ có điểm đầu là A, điểm cuối là B thì ký hiệu là AB^→.

Ngoài ra, vectơ còn được ký hiệu là: a^→, b^→, x^→, y^→,…

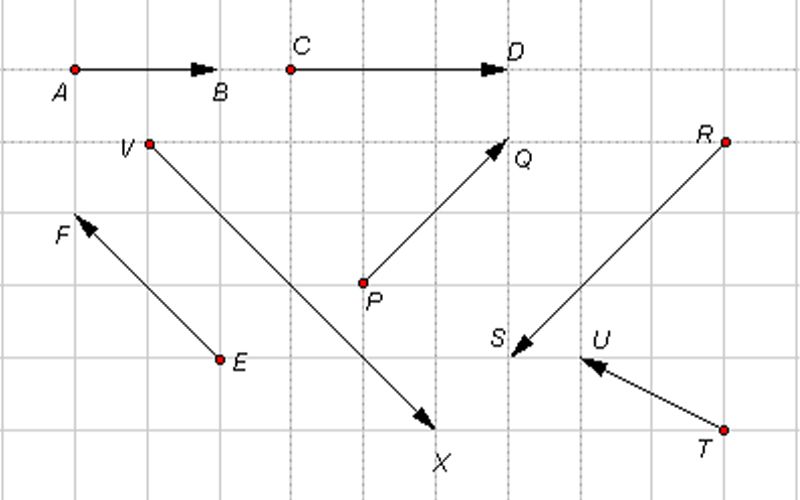
Theo định nghĩa, vectơ là một đoạn thẳng có hướng

Cái loại vectơ

Trong Toán học, ta sẽ bắt gặp các loại vectơ bao gồm: Hai vectơ cùng phương, cùng hướng, hai vectơ bằng nhau và vectơ không. Cùng tìm hiểu chi tiết về định nghĩa, tính chất và ví dụ minh họa về các loại vectơ này nhé!

Hai vectơ cùng phương, cùng hướng

Trong Toán học, hai vectơ cùng phương là hai vectơ có giá song song hoặc trùng với nhau. Giá của một vectơ là một đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.

Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng với nhau.

Điều kiện cần và đủ để hai vectơ a^→ và b^→ (b^→≠0) cùng phương là có một hệ số k sao cho a^→ = kb^→.

Ví dụ minh họa: 

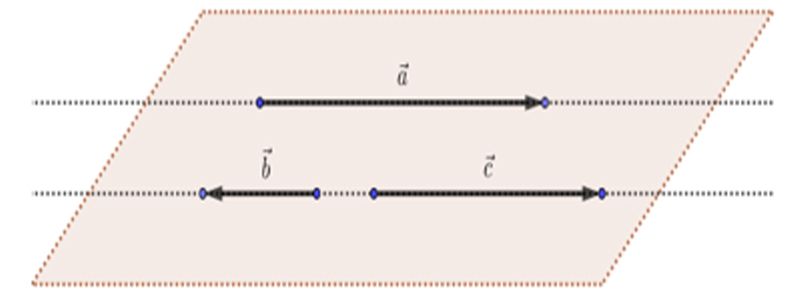
Ví dụ về hai vectơ cùng phương, cùng hướng

Ở hình ảnh trên, ba vectơ a^→, b^→, c^→ cùng phương với nhau. Trong đó, vectơ a^→ cùng hướng với vectơ c^→ và ngược hướng với vectơ b^→.

Hai vectơ bằng nhau

Ngoài phương và hướng của vectơ, ta cũng có thể so sánh, xét hai vectơ đã cho có bằng nhau hay không. Hai vectơ được gọi là bằng nhau khi chúng có cùng hướng và cùng độ dài. Nếu ngược hướng thì sẽ được gọi là hai vectơ đối nhau.

Khi khoảng cách giữa điểm đầu và điểm cuối của hai vectơ bất kỳ bằng nhau thì tức là hai vectơ này bằng nhau.

Ví dụ minh họa: 

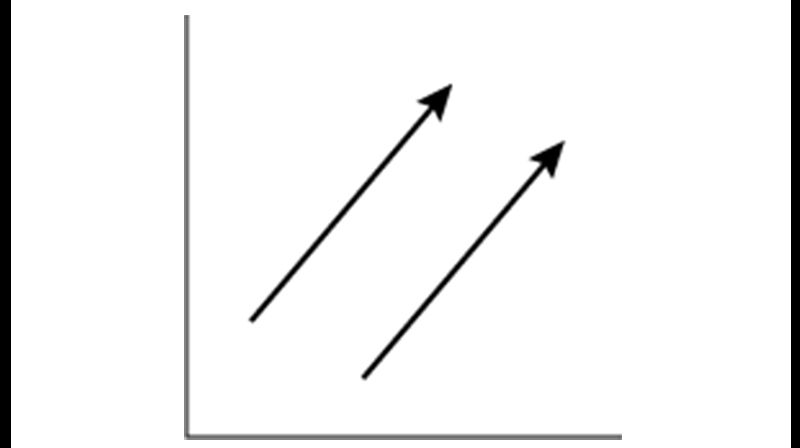
Ví dụ minh họa hai vectơ bằng nhau

Hai vectơ trên có cùng hướng và cùng độ dài. Ta nói hai vectơ này bằng nhau.

Vectơ không

Vectơ không là một loại vectơ khá đặc biệt. Với một điểm A bất kỳ, ta quy ước có một vectơ có điểm đầu và điểm cuối đều là A, và vectơ này được gọi là vectơ không.

Vectơ không được ký hiệu là 0^→, hay AA^→, BB^→,… Vectơ không có cùng phương, cùng hướng với mọi vectơ, và mọi vectơ không đều bằng nhau.

Ví dụ minh họa:

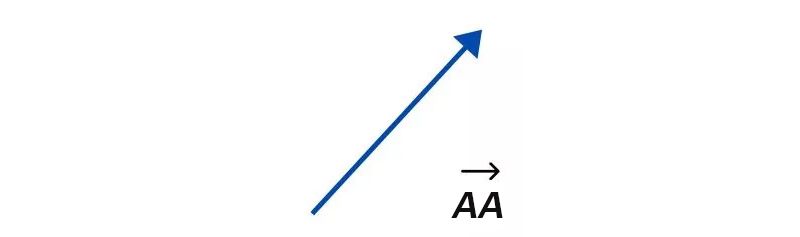
Vectơ không

Từ điểm A này, ta có vectơ không hay vectơ AA^→.

Độ dài một vectơ

Độ dài của một vectơ được định nghĩa là khoảng cách từ điểm đầu đến điểm cuối của vectơ đó. 

Khi xét độ dài của một vectơ, ta cũng chỉ cần dựa vào khoảng cách từ điểm đầu đến điểm cuối. Một vectơ a^→ bất kỳ có ký hiệu độ dài như sau: |a^→|.

Ví dụ minh họa: 

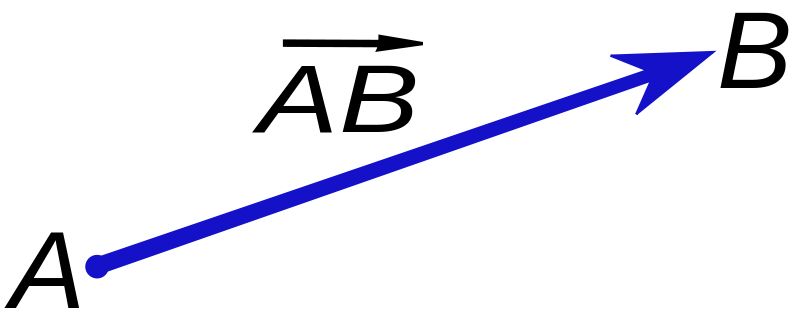
Độ dài vectơ AB^→

Đối với vectơ AB^→, độ dài của vectơ chính là khoảng cách từ điểm A đến điểm B, hay nói cách khác chính là độ dài của đoạn thẳng AB, được ký hiệu là |AB^→|.

Một số bài tập ví dụ về vectơ

Dưới đây là một số dạng bài tập thông dụng về vectơ, mời các bạn cùng tham khảo.

• Bài tập 1: Cho 2 vectơ u^→ = 2a^→ + b^→ và v^→ = -6a^→ – 3b^→. Mệnh đề nào là đúng nhất?

A. Hai vectơ u^→ và v^→ cùng phương

B. Hai vectơ u^→ và v^→ cùng phương và cùng hướng

C. Hai vectơ u^→ và v^→ cùng phương và ngược hướng

D. Hai vectơ u^→ và v^→ không cùng phương

Đáp án: C

• Bài tập 2: Cho 3 vectơ a^→, b^→, c^→ không đồng phẳng. Xét các vectơ x^→ = 2a^→ – b^→, y^→ = -4a^→ + 2b^→, z^→ = -3b^→ – 2c^→. Khẳng định nào dưới đây là chính xác nhất?

A. Hai vectơ y^→, z^→ cùng phương

B. Hai vectơ x^→, y^→ cùng phương

C. Hai vectơ x^→, z^→ cùng phương

D. Ba vectơ x^→, y^→, z^→ đồng phẳng

Đáp án: B

• Bài tập 3: Cho điểm A và vectơ a^→ khác vectơ 0^→. Xác định điểm M sao cho vectơ AM^→ cùng phương với vectơ a^→.

Đáp án: Gọi giá của vectơ a^→ là đường thẳng b.

Trường hợp 1: Điểm A thuộc đường thẳng b

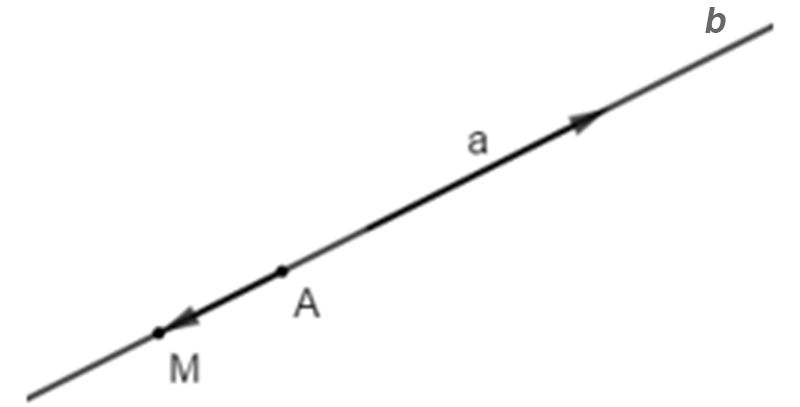
Trường hợp 1

Khi đó, ta lấy một điểm M bất kỳ thuộc đường thẳng b. Khi đó đường thẳng AM = b

Do đó, vectơ AM^→ cùng phương với vectơ a^→

Vậy M thuộc đường thẳng b với b đi qua điểm A và b là giá của vectơ a^→

Trường hợp 2: Điểm A không thuộc đường thẳng b

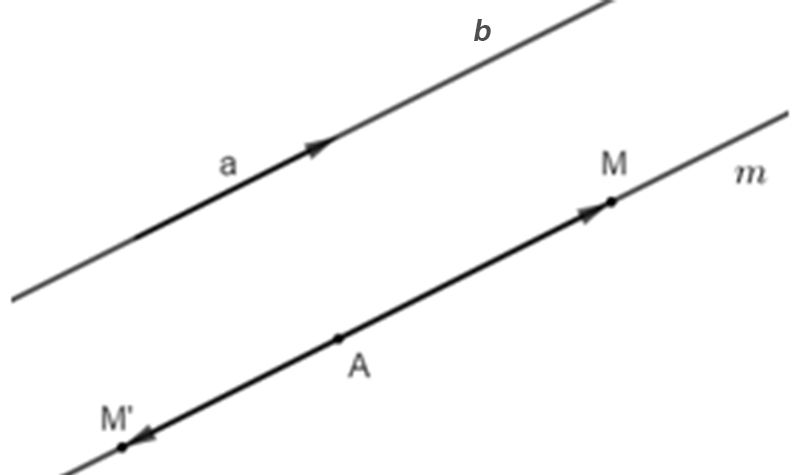
Trường hợp 2

Từ điểm A, ta dựng một đường thẳng m song song với đường thẳng b. Với điểm M bất kỳ thuộc m, ta có AM // b

=>  AM^→ cùng phương với vectơ a^→

Vậy M thuộc đường thẳng m với m đi qua A và m // b

• Bài tập 4: Cho lục giác đều ABCDEF tâm O. Cho biết có bao nhiêu vectơ khác không, cùng phương với vectơ OB^→ có điểm đầu và điểm cuối là các đỉnh của lục giác?

Đáp án:

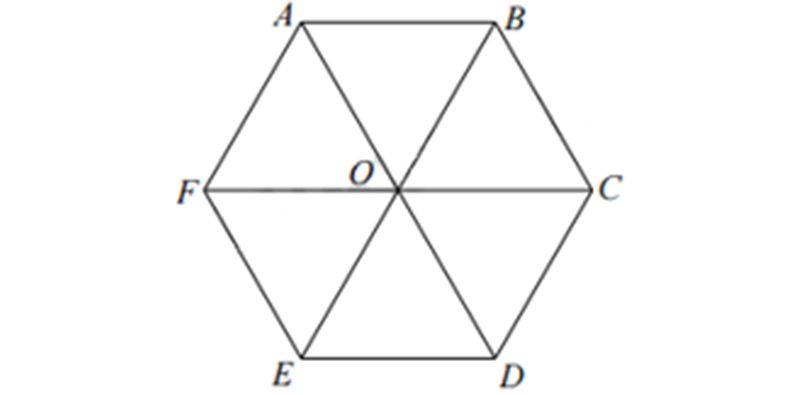
Hình lục giác đều ABCDEF tâm O

ABCDEF là lục giác đều tâm O => BE // CD // AF => OB // CD // AF

Do đó, các vectơ cùng phương với vectơ OB^→ có điểm đầu và điểm cuối là các đỉnh của lục giác là: BE^→, EB^→, CD^→, DC^→, AF^→, FA^→

Vậy có tổng cộng là 6 vectơ

• Bài tập 5: Chứng minh rằng hai vectơ bằng nhau có chung điểm đầu (hoặc điểm cuối) thì chúng có chung điểm cuối (hoặc điểm đầu).

Đáp án: Giả sử ta có: AB^→ = AC^→. Khi đó AB = AC, ba điểm A, B, C thẳng hàng. B, C thuộc nửa đường thẳng góc A

=> B trùng với C (chứng minh tương tự đối với trường hợp trùng điểm cuối)

• Bài tập 6: Cho 5 điểm A, B, C, D, E. Có bao nhiêu vectơ khác vectơ không có điểm đầu và điểm cuối là các điểm đó?

Đáp án: Có 10 cặp điểm khác nhau gồm: {A,B}, {A,C}, {A,D}, {A,E}, {B,C}, {B,D}, {B,E}, {C,D}, {C,E}, {D,E}. Vậy có 20 vectơ khác vectơ không

Xem thêm:

• Sơ đồ khối là gì? Mục đích, quy tắc và cách vẽ sơ đồ khối chính xác đơn giản nhất
• Số chính phương là gì? Tính chất và bài tập ví dụ minh họa về số chính phương
• Đường tròn nội tiếp tam giác là gì? Tính chất và cách xác định nội tiếp tam giác

Trên đây là tổng hợp những kiến thức về khái niệm vectơ là gì, các loại vectơ và một số dạng bài tập thông dụng. Bạn có thể tham khảo những nội dung này để ôn tập và chuẩn bị cho các bài kiểm tra sắp tới. Chúc bạn luôn đạt được kết quả cao trong học tập!