Thừa số là gì? Thừa số nguyên tố là gi? Cách phân tích một số thành các thừa số

Bao giờ bạn từng tò mò về “Thừa số là gì?” và tại sao chúng lại đóng một vai trò quan trọng đến vậy trong lĩnh vực số học? Mỗi con số đều giữ bí mật của mình, và chúng ta có khả năng “giải mã” chúng thông qua quá trình phân tích thành các thừa số nguyên tố. Trong bài viết này, Bamboo School sẽ bắt đầu một hành trình thú vị, khám phá sâu hơn về thừa số và các bước quan trọng để phân tích chúng một cách chính xác!

Thừa số là gì Thừa số nguyên tố là gi Cách phân tích một số thành các thừa số

Thừa số là gì?

Thừa số, một khái niệm cơ bản trong toán học, đơn giản là những yếu tố cấu thành một số thông qua phép nhân. Mỗi số có thể có nhiều biểu diễn dưới dạng tích của các thừa số khác nhau, tương tự như cách một câu chuyện có thể được kể theo nhiều cách khác nhau với cùng một thông điệp cốt lõi. Xây dựng một số như việc xây nhà từ các “viên gạch” thừa số, mỗi viên là một phần cơ bản, giúp ta hình dung về cách thừa số cấu thành một số lớn.

Ví dụ cụ thể với số 36:

• 36 = 6 x 6 => 6 là thừa số
• 36 = 4 x 9 => 4 và 9 đều là thừa số
• 36 = 3 x 12 => 3 và 12 cũng là thừa số

Những ví dụ này cho thấy một số có thể được biểu diễn bằng nhiều bộ thừa số khác nhau, giúp ta nhận thức sâu hơn về cấu trúc và tính chất của số. Điều này cũng hỗ trợ trong việc phân tích và giải quyết các bài toán toán học một cách linh hoạt.

Thừa số nguyên tố là gì?

Mỗi số tự nhiên lớn hơn 1 đều có thể phân tích thành dạng tích của các số nguyên tố. Những số nguyên tố này được gọi là “thừa số nguyên tố” của số đó.

Cụ thể như sau:

• Số nguyên tố: Một số nguyên tố là số tự nhiên lớn hơn 1 chỉ chia hết cho 1 và chính nó. Ví dụ, 2, 3, 5, và 7 đều là số nguyên tố vì chúng không chia hết cho bất kỳ số tự nhiên nào khác ngoài 1 và chính nó.
• Phân tích thừa số: Mỗi số tự nhiên lớn hơn 1 có thể phân tích thành các thừa số nguyên tố. Quá trình này bao gồm việc tách một số thành các số nguyên tố nhỏ hơn một cách liên tiếp cho đến khi chỉ còn lại các số nguyên tố.
• Thừa số nguyên tố: Trong quá trình phân tích thừa số, những số nguyên tố thu được được gọi là thừa số nguyên tố của số ban đầu.

Ví dụ: Xét số 56.

• Đầu tiên, chia 56 cho số nguyên tố nhỏ nhất, là 2, ta được 28.
• Tiếp tục chia 28 cho 2, ta được 14.
• Cuối cùng, chia 14 cho 2 ta được 7, mà 7 là số nguyên tố.

Vậy, 56 có thể biểu diễn dưới dạng 56 = 2 × 2 × 2 × 7. Ở đây, 2 và 7 đều là thừa số nguyên tố của 56.

Cách xác định thừa số nguyên tố

Cách xác định thừa số nguyên tố bao gồm các bước sau:

• Chọn số cần xác định thừa số: Chọn một số tự nhiên lớn hơn 1 mà bạn muốn phân tích thành thừa số nguyên tố.
• Bắt đầu với số nguyên tố nhỏ nhất: Bắt đầu với số nguyên tố nhỏ nhất, thường là 2, và kiểm tra xem số cần phân tích có chia hết cho nó hay không.
• Chia số cho thừa số nguyên tố: Nếu số cần phân tích chia hết cho thừa số nguyên tố, ghi lại thừa số đó và thực hiện phép chia để thu được một số mới.
• Lặp lại quá trình: Tiếp tục quá trình trên với số mới thu được, và lặp lại cho đến khi số không còn chia hết cho bất kỳ thừa số nguyên tố nào nữa.
• Kết hợp các thừa số nguyên tố: Khi không thể chia hết nữa, kết hợp tất cả các thừa số nguyên tố đã thu được để biểu diễn số ban đầu dưới dạng tích của chúng.

Ví dụ: Xét số 48

• Bắt đầu với 2, thấy 48 chia hết cho 2, ghi lại 2 và thu được 48/2 = 24.
• 24 cũng chia hết cho 2, ghi lại thêm 2 và thu được 24/2 = 12.
• 12 chia hết cho 2, ghi lại thêm 2 và thu được 12/2 = 6.
• 6 chia hết cho 2, ghi lại thêm 2 và thu được 6/2 = 3.
• 3 không chia hết cho bất kỳ số nguyên tố nào khác ngoài 3.

Kết quả cuối cùng là 48=2×2×2×2×3.
deneme bonusu veren siteler

Cách xác định thừa số nguyên tố

Cách phân tích một số thành tích của các thừa số

Phân tích số nguyên cơ bản ra thừa số

Bước 1 – Hiểu rõ thừa số là gì:

Trước hết, ta cần nắm vững khái niệm về thừa số. Thừa số là những số tự nhiên, khi nhân với nhau, tạo ra một số cụ thể. Mọi số nguyên đều có thể được phân tích thành tích của các thừa số.

Bước 2 – Bắt đầu với số nhỏ nhất:

Chọn số nguyên tố nhỏ nhất, thường là 2, và thử chia số cần phân tích cho số đó. Nếu chia hết, ghi nhận số nguyên tố đó là một thừa số.

Bước 3 – Lặp lại quá trình:

Sau khi xác định một thừa số, chia số ban đầu cho thừa số đó để thu được một số mới. Tiếp tục quá trình này cho đến khi số mới không chia hết cho bất kỳ số nguyên tố nào khác.

Bước 4 – Kiểm tra các số nguyên tố tiếp theo:

Nếu số cần phân tích không chia hết cho số nguyên tố đang xét, chuyển sang số nguyên tố tiếp theo và thử chia. Lặp lại quá trình này cho đến khi phân tích hoàn toàn số ban đầu.

Bước 5 – Kết hợp các thừa số:

Cuối cùng, kết hợp tất cả các thừa số nguyên tố đã tìm ra để biểu diễn số ban đầu dưới dạng tích của chúng.

Hãy xem xét việc phân tích số 72 thành các thừa số như sau:

Bước đầu tiên, chúng ta chọn số nguyên tố đầu tiên là 2. Vì 72 chia hết cho 2, ta biết rằng 2 là một thừa số. Khi chia 72 cho 2, chúng ta thu được một số mới là 36.

Tiếp theo, số 36 vẫn chia hết cho 2. Vậy 2 là thừa số tiếp theo. Khi chia 36 cho 2, chúng ta thu được 18.

Tiếp tục, số 18 cũng chia hết cho 2. Vậy 2 cũng là thừa số tiếp theo. Khi chia 18 cho 2, chúng ta thu được 9.

Tuy nhiên, số 9 không chia hết cho 2. Vì vậy, chúng ta chuyển sang số nguyên tố tiếp theo là 3. 9 chia hết cho 3, cho ta thừa số tiếp theo là 3.

Kết quả cuối cùng, số 72 có thể được biểu diễn dưới dạng 72 = 2 x 2 x 2 x 3 x 3 hoặc 72 = 2^3 x 3^2.

Cách phân tích các số lớn thành thừa số

Phân tích các số lớn thành thừa số là một quy trình quan trọng trong toán học. Dưới đây là hướng dẫn chi tiết:

• Xác định điểm khởi đầu:
  • Bắt đầu bằng cách chia số lớn cho các số nguyên tố nhỏ nhất, như 2, 3, 5, v.v.
  • Nếu số ban đầu là chẵn, thì số nguyên tố đầu tiên là 2.
• Tiến trình chia:
  • Mỗi lần chia, ghi nhận số nguyên tố đó và tiếp tục chia thương cho số nguyên tố đó cho đến khi không chia hết nữa.
• Chuyển sang số nguyên tố tiếp theo:
  • Sau khi không chia hết nữa, chuyển sang số nguyên tố tiếp theo và lặp lại quá trình.
• Xác định số lẻ:
  • Đối với số lẻ, thử chia cho các số nguyên tố bắt đầu từ 3 và tiếp tục với các số nguyên tố cao hơn.
• Xác minh kết quả:
  • Khi thương cuối cùng là 1, bạn đã tìm ra tất cả thừa số.
  • Nhân tất cả thừa số đã tìm được để đảm bảo kết quả trùng khớp với số ban đầu.

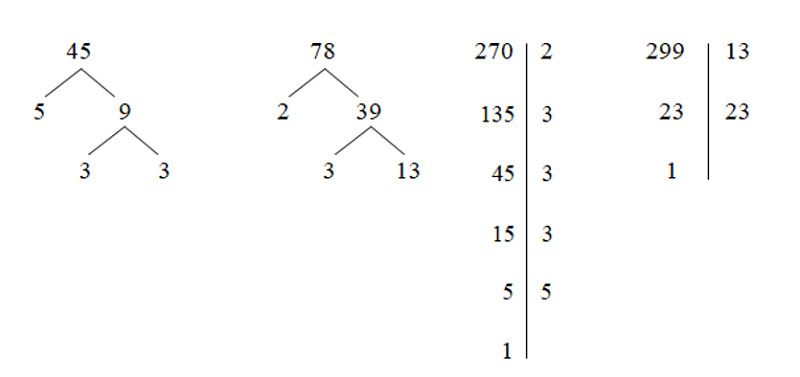
Ví dụ: Phân tích số 1260 thành thừa số?

Chúng ta có thể phân tích số 1260 thành các thừa số như sau:

• Bước 1: Xác định số nguyên tố đầu tiên để chia. Vì 1260 là một số chẵn, ta bắt đầu bằng việc chia cho 2. 1260 : 2 = 630.
• Bước 2: Số thu được sau khi chia, 630, vẫn là một số chẵn. Tiếp tục chia cho 2. 630 : 2 = 315.
• Bước 3: Số 315 không chia hết cho 2, ta thử chia cho số nguyên tố tiếp theo là 3. 315 : 3 = 105.
• Bước 4: Tiếp tục chia 105 cho số nguyên tố tiếp theo. 105 : 3 = 35.
• Bước 5: Chia số 35 cho số nguyên tố tiếp theo là 5. 35 : 5 = 7.
• Bước 6: Số 7 là một số nguyên tố, không thể chia tiếp.

Kết luận: Số 1260 có thể phân tích thành tích các thừa số nguyên tố là 2 × 2 × 3 × 3 × 5 × 7, hoặc viết dưới dạng lũy thừa là 2^2 x 3^2 x 5 x 7.

Ý nghĩa của việc xác định thừa số là gì

Việc phân tích số thành thừa số là một kiến thức Toán học cơ bản và quan trọng, mang lại sự hiểu biết về bản chất và ý nghĩa của phép nhân. Nó không chỉ giúp chúng ta hiểu cấu trúc số mà còn nhìn nhận giá trị của một số thông qua các thừa số.

Ứng dụng của việc xác định thừa số không chỉ giới hạn trong Toán học cơ bản mà còn mở rộng vào đại số, tích phân và các lĩnh vực cao cấp khác. Kiến thức về thừa số giúp chúng ta phát triển tư duy logic và hiểu sâu hơn về các khái niệm trong toán học.

Quá trình xác định giá trị của phép nhân và phân tích tích thành các thừa số là cách học xuôi và ngược, đều quan trọng trong quá trình giáo dục. Việc này giúp chúng ta phát triển kỹ năng logic và tìm kiếm nhiều cách tiếp cận để giải quyết vấn đề, nâng cao khả năng sáng tạo và hiệu quả học tập.

Lưu ý khi thực hiện phân tích thừa số là gì

Phân tích số thành các thừa số nguyên tố là quá trình tách một số thành các yếu tố nguyên tố nhỏ nhất. Để thực hiện điều này một cách chính xác và hiệu quả, quan trọng để:

• Hiểu rõ khái niệm thừa số: Thừa số là số tự nhiên chia hết cho số đang xét mà không dư. Số nguyên tố chỉ chia hết cho 1 và chính nó.
• Sử dụng các số nguyên tố nhỏ trước: Bắt đầu quá trình phân tích bằng cách chia cho các số nguyên tố nhỏ như 2, 3, 5, 7… để loại bỏ thừa số nhanh chóng.
• Không xét số âm: Chỉ xét các số dương và xem xét giá trị tuyệt đối cho số âm.
• Ghi chép rõ ràng: Ghi lại mỗi bước thực hiện để tránh bỏ sót bất kỳ thừa số nào.
• Kiểm tra kỹ: Xác minh lại bằng cách nhân tất cả thừa số để đảm bảo tích đúng bằng số ban đầu.
• Sử dụng mẹo và kỹ thuật: Áp dụng các mẹo như kiểm tra tổng chữ số chia hết cho 9 để nhanh chóng xác định thừa số.
• Luyện tập thường xuyên: Thực hành thường xuyên giúp nắm vững kỹ thuật và phát hiện các thừa số một cách nhanh chóng.

Dạng bài tập vận dụng thường gặp

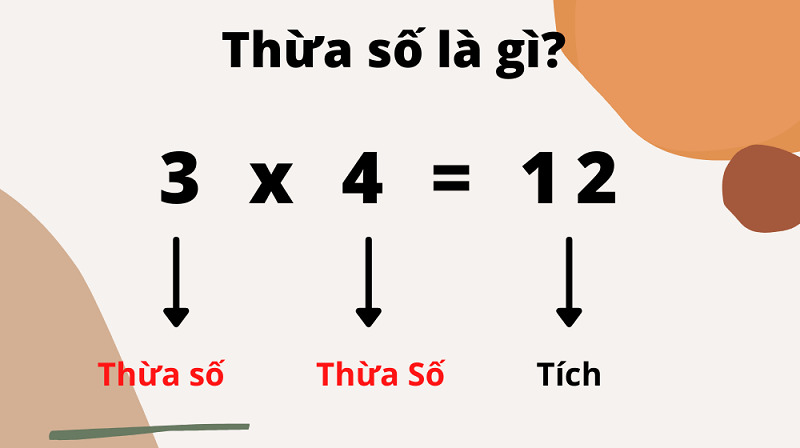
Dạng 1: Xác định giá trị của thừa số và tích trong phép nhân

Một khái niệm cơ bản trong toán học là hiểu rõ về “thừa số” và “tích”. Thừa số là những số được nhân với nhau để tạo ra một tích. Trong một phép nhân, số bạn nhân gọi là thừa số, và kết quả của phép nhân được gọi là tích.

Ví dụ: Xét phép nhân: 4 × 5 = 20.

Trong trường hợp này:

• 4 và 5 chính là thừa số của phép nhân.
• 20 là tích, tức là kết quả của việc nhân 4 với 5.

Dạng 2: Tính giá trị của tích

Để tính giá trị của tích một cách trực quan và dễ dàng, ta có thể chuyển phép nhân về dạng tổng của nhiều số hạng giống nhau.

Ví dụ, hãy xem xét phép nhân 4 × 3.

Để tính giá trị của tích này, chúng ta có thể coi đó như việc cộng số 4 với chính nó 3 lần: 4 × 3 = 4 + 4 + 4 = 12.

Ở đây:

• 4 và 3 là các thừa số của phép nhân.
• 12 là tích, tức là kết quả khi nhân 4 với 3.

Qua cách biểu diễn này, việc tính giá trị của tích trở nên dễ dàng và trực quan hơn, giúp học sinh hiểu cơ bản về phép nhân. Điều quan trọng khác là học sinh có thể nhìn thấy mối liên hệ giữa phép nhân và phép cộng, giúp họ hiểu rõ hơn về cấu trúc và tính chất của các phép toán.

Dạng 3: Toán đố (bài toán có lời văn)

Bài toán lời văn, hay còn được gọi là toán đố, đặt ra những thách thức đòi hỏi học sinh không chỉ sử dụng kiến thức về toán học mà còn cần tư duy logic và phân tích thông tin. Để giải quyết những bài toán này, việc hiểu rõ về khái niệm “thừa số” và cách áp dụng nó vào bài toán là vô cùng quan trọng.
deneme bonusu
Ví dụ:

An có một hộp bi. Mỗi ngày, cô ấy mua thêm 3 bi và thêm vào hộp. Sau 4 ngày, An có tổng cộng bao nhiêu bi mới?

Hướng dẫn:

Để giải bài toán, ta cần xác định thừa số chính trong đề bài. Trong trường hợp này, thừa số là số bi mà An mua mỗi ngày (3 bi) và số ngày An mua bi (4 ngày).

Sử dụng kiến thức về phép nhân, ta có:

Số bi mới sau 4 ngày là: 3 (bi/ngày) x 4 (ngày) = 12 (bi)

Vậy, sau 4 ngày, An có thêm 12 bi mới vào hộp của mình.

Hi vọng bài viết đã hướng dẫn các em biết cách phân tích thừa số nguyên tố, giúp các em hiểu sâu về cấu trúc và tính chất của các số tự nhiên. Chúc các em thành công!