Cực trị là gì? Đây là khái niệm quan trọng trong toán học đại số THPT. Để hiểu cực trị là gì và vận dụng nó hãy cùng Bamboo School tìm hiểu nhé!

cực trị là gì
Cực trị của hàm số là gì? Cực trị là gì?
Cực trị của hàm số là giá trị khiến hàm số đổi chiều khi biến thiên. Trình bày theo hình học, ta sẽ thấy nó biểu diễn khoảng cách lớn nhất từ điểm này sang điểm kia và khoảng cách nhỏ nhất từ điểm này sang điểm nọ.
Chú ý: Giá trị cực đại và giá trị cực tiểu KHÔNG PHẢI là giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Định nghĩa về giá trị cực đại và giá trị cực tiểu
Cực trị là gì? Hãy cùng tìm hiểu qua giả sử: hàm số f xác định trên K (K ⊂ ℝ) và x0 ∈ K.
x0 được gọi là điểm cực đại của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) < f(x0), ∀ x ∈ (a;b) \{x0}. Khi đó f(x0) được gọi là giá trị cực đại của hàm số f.
x0 được gọi là điểm cực tiểu của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) > f(x0), ∀ x ∈ (a;b) \{x0}. Khi đó f(x0) được gọi là giá trị cực tiểu của hàm số f.
Điểm cực đại (cực tiểu) x0 được gọi chung là điểm cực trị. Giá trị cực đại (cực tiểu) f(x0) của hàm số được gọi chung là cực trị. Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp K.
Nói chung, giá trị cực đại (cực tiểu) f(x0) không phải là giá trị lớn nhất (nhỏ nhất) của hàm số f trên tập K; f(x0) chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số f trên một khoảng (a;b) chứa x0.
Nếu x0 là một điểm cực trị của hàm số f thì điểm (x0; f(x0)) được gọi là điểm cực trị của đồ thị hàm số f.
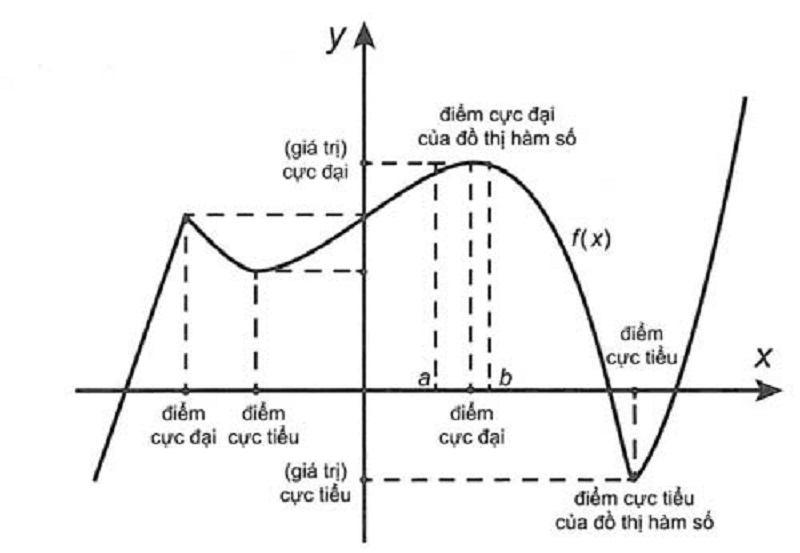
Hình ảnh: Minh họa cho điểm cực đại và cực tiểu của hàm số
Các định lý về cực trị hàm số
Điều kiện cần để hàm số đạt cực trị:
Định lí 1
Giả sử hàm số f đạt cực trị tại điểm x0. Khi đó, nếu f có đạo hàm tại điểm x0 thì f’(x0) = 0.
Chú ý:
1) Điều ngược lại có thể không đúng. Đạo hàm f’ có thể = 0 tại điểm x0 nhưng hàm số f không đạt cực trị tại điểm x0.
2) Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.
Định lý 2
a) Nếu f’(x) đổi dấu từ âm sang dương khi x đi qua điểm x0 (theo chiều tăng) thì hàm số đạt cực tiểu tại x0.
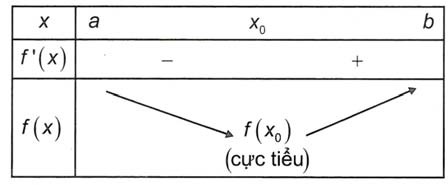
b) Nếu f’(x) đổi dấu từ dương sang âm khi x đi qua điểm x0 (theo chiều tăng) thì hàm số đạt cực đại tại x0.

Định lí 3
Giả sử hàm số f có đạo hàm cấp một trên khoảng (a;b) chứa điểm x0, f’(x0) = 0 và f có đạo hàm cấp hai khác 0 tại điểm x0.
a) Nếu f’’(x0) < 0 thì hàm số f đạt cực đại tại điểm x0.
b) Nếu f’’(x0) > 0 thì hàm số f đạt cực tiểu tại điểm x0.
c) Nếu f’’(x0) = 0 thì ta chưa thể kết luận được, cần lập bảng biến thiên hoặc bảng xét dấu đạo hàm.
Cách tìm điểm cực trị của hàm số
Mỗi hàm số đều có một tính chất và cách tìm cực trị khác nhau. Ngay sau đây Monkey sẽ giới thiệu đến bạn cách xác định điểm cực trị của dạng hàm số thường gặp trong các đề thi.
Tìm cực trị của hàm số bậc 2
Hàm số bậc 2 có dạng: y = ax2 + bx + c (a ≠ 0) với miền xác định là D = R. Ta có: y’ = 2ax + b.
y’ đổi dấu khi x qua x0 = -b/2a
Hàm số đạt cực trị tại x0 = -b/2a
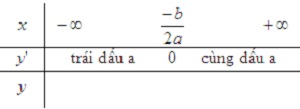
Xác định điểm cực trị của hàm số bậc 3
Hàm số bậc 3 có dạng: y = ax3 + bx2 + cx + d (a ≠ 0) với miền xác định là D = R. Ta có: y’ = 3ax2 + 2bx + c → Δ’ = b2 – 3ac.
- Δ’ ≤ 0 : y’ không đổi dấu → hàm số không có cực trị
- Δ’ > 0 : y’ đổi dấu 2 lần → hàm số có hai cực trị (1 CĐ và 1 CT)
Cách tìm đường thẳng đi qua hai điểm cực trị của hàm số bậc ba:
Ta có thể phân tích : y = f(x) = (Ax + B)f ‘(x) + Cx + D bằng cách chia đa thức f(x) cho đa thức f ‘(x).
Giả sử hàm số đạt cực trị tại x1 và x2
Ta có: f(x1) = (Ax1 + B)f ‘(x1) + Cx1 + D → f(x1) = Cx1 + D vì f ‘(x1) = 0
Tương tự: f(x2) = Cx2 + D vì f ‘(x2) = 0
Kết luận: Đường thẳng qua hai điểm cực trị có phương trình: y = Cx + D
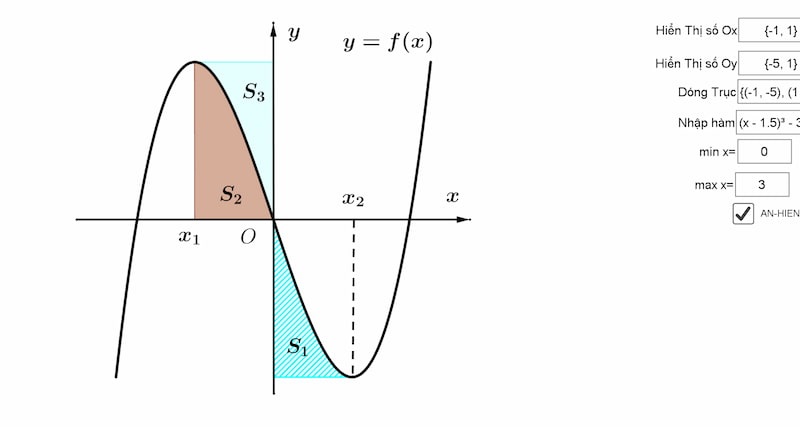
Cách tìm đường thẳng đi qua hai điểm cực trị của hàm số bậc ba
Cách tính cực trị của hàm số bậc 4 (Hàm trùng phương)
Hàm số trùng phương có dạng: y = ax4 + bx2 + c (a ≠ 0) với miền xác định là D = R. Ta có: y’ = 4ax^3 + 2bx = 2x(2ax^2 + b) và y’ = 0 x = 0 2ax^2 + b = 0 x = 0 x62 = -b/2a.
- Khi -b/2a ≤ 0 ⇔ b/2a ≥ 0 thì y’ chỉ đổi dấu 1 lần khi x đi qua x0 = 0 → Hàm số đạt cực trị tại xo = 0
- Khi -b/2a > 0 ⇔ b/2a < 0 thì y’ đổi dấu 3 lần → hàm số có 3 cực trị
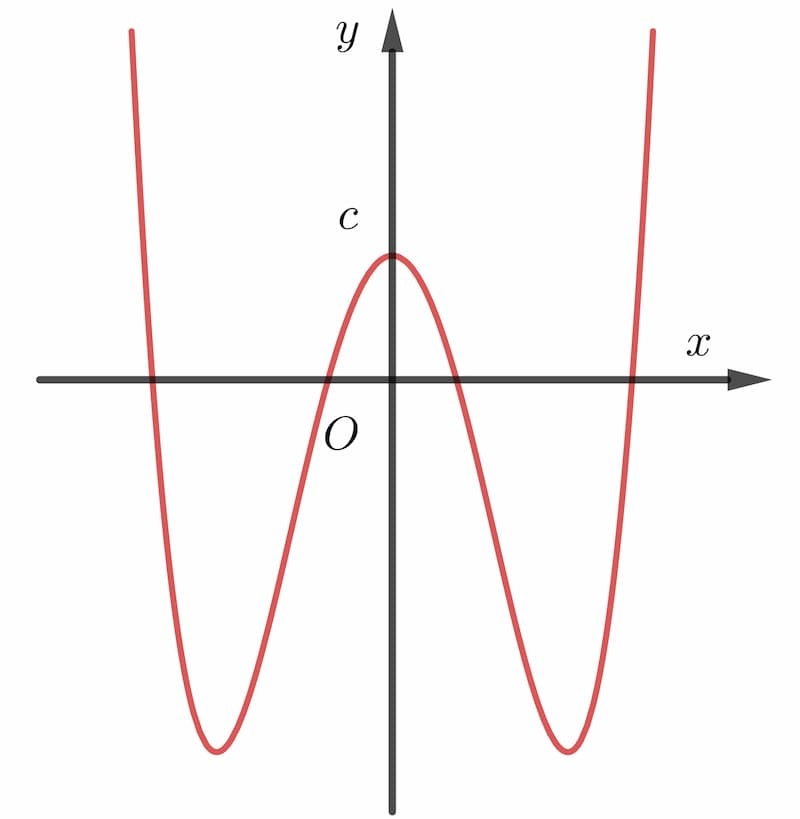
Cách tính cực trị của hàm số bậc 4 (Hàm trùng phương)
Cách xác định cực trị của hàm số lượng giác
Phương pháp tìm cực trị của hàm số lượng giác như sau:
Bước 1: Tìm miền xác định của hàm số.
Bước 2: Tính đạo hàm y’ = f’(x), giải phương trình y’=0, giả sử có nghiệm x=x0.
Bước 3: Khi đó ta tìm đạo hàm y’’.
Tính y’’(x0) rồi đưa ra kết luận dựa vào định lý 2.
Các dạng bài tập tìm điểm cực trị hàm số thường gặp
Dạng 1: Tìm điểm cực trị của hàm số
Có 2 cách thức để giải dạng bài toán tìm số điểm cực trị của hàm số, bạn có thể theo dõi ngay bên dưới đây.
Cách 1:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính f'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3: Lập bảng biến thiên.
Bước 4: Từ bảng biến thiên suy ra các điểm cực trị.
Cách 2:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Tính f'(x). Giải phương trình f'(x)và ký hiệu xi (i=1,2,3,…)là các nghiệm của nó.
Bước 3: Tính f”(x) và f”(xi ) .
Bước 4: Dựa vào dấu của f”(xi )suy ra tính chất cực trị của điểm xi.
Dạng 2: Tìm tham số m để hàm số đạt cực trị tại một điểm
Phương pháp giải:
Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0. Khi đó để giải bài toán này, ta tiến hành theo hai bước.
Bước 1: Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .
Bước 2: Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?
Dạng 3: Biện luận theo m số cực trị của hàm số
Đối với cực trị của hàm số bậc ba
Cho hàm số y = ax^3 + bx^2 + cx + d, a ≠ 0. Khi đó, ta có: y’ = 0 ⇔ 3ax^2 + 2bx + c = 0 (1) ; Δ’y’ = b^2 – 3ac.
Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
Hàm số bậc 3 không có cực trị ⇔ b^2 – 3ac ≤ 0
Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
Hàm số bậc 3 có 2 cực trị ⇔ b^2 – 3ac > 0
Đối với cực trị của hàm số bậc bốn
Cho hàm số: y = ax^4 + bx^2 + c (a ≠ 0) có đồ thị là (C). Khi đó, ta có: y’ = 4ax^3 + 2bx; y’ = 0 ⇔ x = 0 hoặc x^2 = -b/2a.
(C) có một điểm cực trị y’ = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
(C) có ba điểm cực trị y’ = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Kết luận
Trên đây là tất cả những thông tin giúp trả lời cho câu hỏi cực trị là gì. Hy vọng sau những kiến thức được chia sẻ tại bambooschool.edu.vn sẽ có ích cho việc học tập của các em, chúc các em học tập thật tốt











