2 Phương Pháp Giải Phương Trình Bậc Nhất Hai Ẩn: Cách Hiểu và Giải Quyết Đơn Giản Cho Học Sinh

Khi nhắc đến “phương trình bậc nhất hai ẩn,” nhiều học sinh thường cảm thấy lo lắng và e ngại. Có lẽ vì các em nghĩ rằng đây là một chủ đề phức tạp, đòi hỏi nhiều kỹ năng tính toán khó nhằn. Nhưng thực tế, nếu được hướng dẫn đúng cách và tiếp cận một cách tự nhiên, phương trình bậc nhất hai ẩn sẽ trở nên vô cùng đơn giản và thậm chí còn rất thú vị.

Vậy nên, nếu bạn đang cảm thấy bối rối với phương trình bậc nhất hai ẩn, đừng lo lắng! Bài viết này sẽ giúp bạn hiểu rõ hơn về chủ đề này, đồng thời mang đến những phương pháp học tập hiệu quả mà Bamboo School đang áp dụng để giúp học sinh chinh phục môn toán một cách dễ dàng và vui vẻ. Hãy cùng bắt đầu nhé!

Phương Trình Bậc Nhất Hai Ẩn Là Gì?

Phương trình bậc nhất hai ẩn

Định nghĩa đơn giản

Phương trình bậc nhất hai ẩn là một phương trình có dạng:

ax+by=c

Trong đó, a, b và c là các hằng số cố định, còn x và y là hai biến số cần tìm.

Ví dụ minh họa cụ thể

Giả sử bạn đi chợ và muốn mua hai loại trái cây: táo và cam. Mỗi quả táo có giá 2.000 đồng và mỗi quả cam có giá 3.000 đồng. Nếu bạn chi tổng cộng 20.000 đồng để mua trái cây, chúng ta có thể thiết lập phương trình bậc nhất hai ẩn để biểu diễn mối quan hệ giữa số lượng táo (x) và số lượng cam (y).

Phương trình sẽ là:

2000x+3000y=20000

Để đơn giản, chia cả hai vế của phương trình cho 1000, ta được:

2x + 3y=20

Phương trình này cho thấy rằng, với số tiền 20.000 đồng, số lượng táo và cam bạn mua phải thoả mãn mối quan hệ 2x + 3y = 20. Ví dụ, nếu bạn mua 4 quả táo (x = 4), ta có:

2(4)+3y=20

-> 8+3y=20

-> 3y=12

-> y=4

Vậy bạn sẽ mua 4 quả táo và 4 quả cam.

Ví dụ này giúp các em học sinh hình dung rõ ràng cách thức áp dụng phương trình bậc nhất hai ẩn trong cuộc sống hàng ngày, qua đó hiểu được tầm quan trọng của việc quản lý ngân sách và vận dụng kiến thức toán học vào thực tiễn.

Mình thường dùng ví dụ về mua đồ ăn để giúp học sinh dễ hình dung hơn. Các em thường rất hào hứng khi nghĩ rằng toán học có thể áp dụng trực tiếp vào cuộc sống hàng ngày. Điều đó không chỉ làm cho bài toán trở nên sinh động mà còn giúp các em hiểu rõ hơn về cách thức vận dụng kiến thức vào thực tiễn.

Qua đó, phương trình bậc nhất hai ẩn không chỉ là một công cụ toán học mà còn là một phương tiện hữu ích để giải quyết các bài toán liên quan đến cuộc sống thường nhật.

Cách Giải Phương Trình Bậc Nhất Hai Ẩn

Khi bắt đầu làm quen với phương trình bậc nhất hai ẩn, điều quan trọng nhất là hiểu rõ các phương pháp giải cơ bản. Hai phương pháp phổ biến nhất mà học sinh cần nắm vững là phương pháp thế và phương pháp cộng đại số. Dưới đây, mình sẽ hướng dẫn từng bước cụ thể kèm ví dụ minh họa để các bạn dễ dàng áp dụng.

Phương Pháp Thế

Phương pháp này giúp chúng ta “thế” một ẩn từ phương trình này sang phương trình kia, từ đó giảm số ẩn và tìm ra nghiệm.

Ví dụ minh họa

Giải hệ phương trình:

Phương Pháp Cộng Đại Số

Phương pháp này giúp chúng ta loại bỏ một ẩn bằng cách cộng hoặc trừ hai phương trình với nhau.

Các bước thực hiện

Ví dụ minh họa

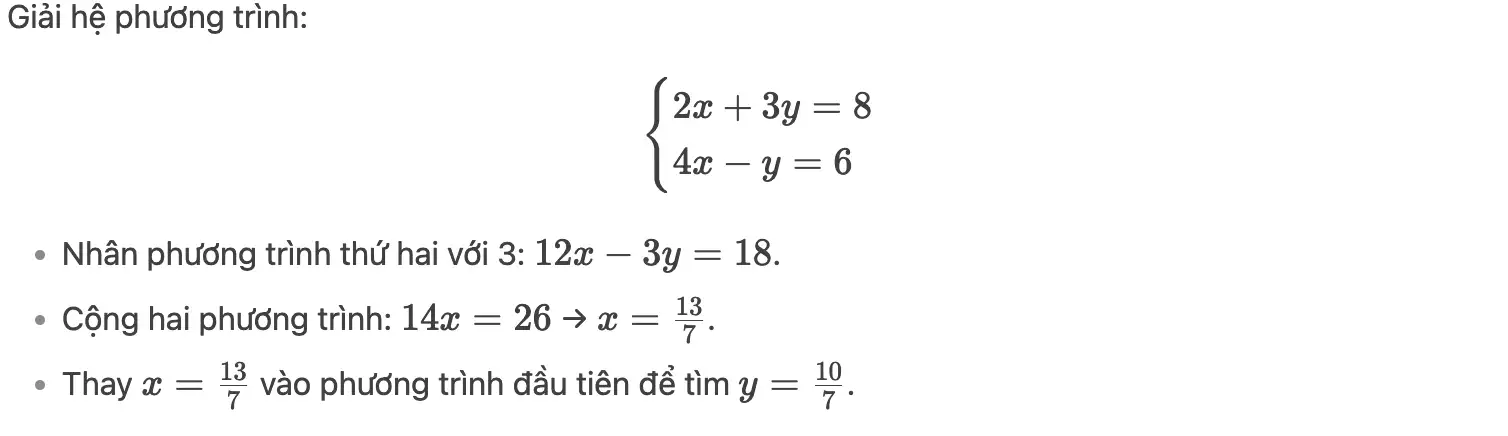
Mình luôn khuyến khích học sinh thử nhiều cách giải khác nhau khi làm quen với phương trình hai ẩn. Đôi khi, các em sẽ tìm ra cách giải riêng mà mình chưa từng nghĩ đến. Đó chính là điều tuyệt vời của toán học – không chỉ có một con đường để đi đến đáp án, mà còn có rất nhiều cách sáng tạo khác nhau.

Ví dụ, có học sinh đã chia sẻ với mình rằng các em thích phương pháp thế hơn vì nó trực quan và dễ hiểu. Trong khi đó, một số em lại thấy phương pháp cộng đại số nhanh gọn hơn. Điều quan trọng là các em cảm thấy thoải mái và tự tin với phương pháp mình chọn. Tại Bamboo School, chúng mình luôn tôn trọng sự sáng tạo và khuyến khích học sinh khám phá cách học phù hợp nhất với bản thân.

Ứng Dụng Thực Tế Của Phương Trình Bậc Nhất Hai Ẩn

Toán học không chỉ là những con số và công thức khô khan trên sách vở, mà nó còn có thể áp dụng vào rất nhiều tình huống thực tế trong cuộc sống. Phương trình bậc nhất hai ẩn cũng vậy – nó giúp chúng ta giải quyết những bài toán thường ngày một cách dễ dàng và hiệu quả. Dưới đây là một số ví dụ thực tế mà bạn có thể gặp phải, cùng cách áp dụng phương trình hai ẩn để tìm ra lời giải.

Ứng Dụng Trong Tính Toán Chi Tiêu

Giả sử bạn muốn mua sách và đồ dùng học tập với một ngân sách nhất định. Bạn có thể sử dụng phương trình hai ẩn để tính toán số lượng mỗi món đồ cần mua sao cho vừa đủ tiền.

Ví dụ cụ thể

Giả sử bạn có 200.000 đồng để mua sách và bút.
Giá một quyển sách là 40.000 đồng, giá một cây bút là 10.000 đồng.
Bạn muốn mua tổng cộng 8 món đồ (sách và bút).

Ứng Dụng Trong Lập Kế Hoạch

Phương trình hai ẩn cũng rất hữu ích khi bạn cần lập kế hoạch cho các hoạt động hàng ngày. Ví dụ, bạn muốn phân chia thời gian giữa học tập và giải trí sao cho hiệu quả nhất.

Ví dụ cụ thể:

Bạn có 5 giờ mỗi ngày để phân chia giữa học bài và xem phim.
Mỗi giờ học bài giúp bạn hoàn thành 2 bài tập, mỗi giờ xem phim giúp bạn thư giãn.
Bạn muốn hoàn thành ít nhất 6 bài tập trong ngày.

Mình thường kể cho học sinh nghe về lần đầu tiên mình áp dụng phương trình hai ẩn để tính toán chi tiêu khi đi du lịch. Hồi đó, mình và nhóm bạn muốn lên kế hoạch chi tiêu cho chuyến đi 3 ngày 2 đêm với ngân sách có hạn. Chúng mình cần tính toán số tiền cho khách sạn, ăn uống, và vé tham quan sao cho vừa đủ mà không bị vượt quá ngân sách.

Bamboo School Đồng Hành Cùng Học Sinh

Tại Bamboo School, chúng tôi hiểu rằng mỗi học sinh đều có một cách tiếp cận kiến thức riêng. Vì vậy, chúng tôi không chỉ tập trung vào việc truyền đạt lý thuyết mà còn chú trọng đến việc áp dụng kiến thức vào thực tế, giúp các em hiểu sâu và nhớ lâu hơn.

Phương Pháp Giảng Dạy Hiện Đại

Các bài học tại Bamboo School luôn được thiết kế để học sinh có cơ hội áp dụng ngay vào các tình huống thực tế.

Kết hợp lý thuyết và thực hành: Các bài học tại Bamboo School luôn được thiết kế để học sinh có cơ hội áp dụng ngay vào các tình huống thực tế. Ví dụ, khi học về phương trình bậc nhất hai ẩn, các em sẽ được thực hành qua các bài toán liên quan đến chi tiêu, lập kế hoạch, hoặc thậm chí là các trò chơi toán học thú vị.
Học qua dự án: Học sinh được khuyến khích tham gia các dự án nhỏ, nơi các em có thể tự mình giải quyết vấn đề và trình bày kết quả trước lớp. Điều này không chỉ giúp các em hiểu bài mà còn rèn luyện kỹ năng thuyết trình và làm việc nhóm.

Môi Trường Học Tập Thân Thiện

Mỗi học sinh đều có một lộ trình học tập riêng, phù hợp với khả năng và sở thích của mình.

Hỗ trợ cá nhân hóa: Mỗi học sinh đều có một lộ trình học tập riêng, phù hợp với khả năng và sở thích của mình. Giáo viên tại Bamboo School luôn sẵn sàng lắng nghe và hỗ trợ các em trong mọi tình huống.

Giáo viên tại Bamboo School luôn sẵn sàng lắng nghe và hỗ trợ các em trong mọi tình huống.

Khơi gợi niềm yêu thích toán học: Chúng tôi tin rằng, khi học sinh cảm thấy thoải mái và được truyền cảm hứng, việc học sẽ trở nên dễ dàng và thú vị hơn bao giờ hết.

Tại Bamboo School, chúng mình luôn cố gắng tạo ra một môi trường học tập mà mỗi học sinh cảm thấy được lắng nghe và hỗ trợ. Mình tin rằng, khi các em cảm thấy thoải mái, việc học sẽ trở nên dễ dàng hơn bao giờ hết.

Mình còn nhớ có một học sinh từng rất sợ học toán, đặc biệt là những bài toán liên quan đến phương trình. Nhưng sau một thời gian được học trong môi trường thân thiện và được khuyến khích sáng tạo, em ấy đã dần tự tin hơn và thậm chí còn trở thành một trong những học sinh xuất sắc nhất lớp. Đó chính là điều mà Bamboo School luôn hướng đến – giúp mỗi học sinh khám phá tiềm năng của bản thân và yêu thích việc học.

Kết Luận

Phương trình bậc nhất hai ẩn không hề khó như nhiều người vẫn nghĩ. Chỉ cần hiểu đúng cách và biết cách áp dụng vào thực tế, các em học sinh hoàn toàn có thể chinh phục dạng toán này một cách dễ dàng. Và quan trọng hơn, toán học không chỉ là những con số khô khan mà còn là công cụ hữu ích giúp chúng ta giải quyết nhiều vấn đề trong cuộc sống.

Tại Bamboo School, chúng tôi luôn sẵn sàng đồng hành cùng học sinh và phụ huynh trên hành trình chinh phục tri thức. Với phương pháp giảng dạy hiện đại, môi trường học tập thân thiện, và đội ngũ giáo viên tận tâm, chúng tôi tin rằng mỗi học sinh đều có thể tỏa sáng theo cách riêng của mình.

Hãy cùng Bamboo School khám phá thế giới toán học đầy màu sắc! Đăng ký ngay để nhận tư vấn và trải nghiệm phương pháp học tập hiệu quả. Chúng tôi sẽ đồng hành cùng bạn trên hành trình chinh phục những đỉnh cao tri thức!