Top 5 bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10

Bí quyết đạt điểm 9-10 môn toán

Kỳ thi tuyển sinh lớp 10 là một trong những cột mốc quan trọng trong cuộc đời học sinh. Môn Toán, với yêu cầu về khả năng tư duy logic và khả năng giải quyết vấn đề, luôn là một môn thi “khó nhằn” đối với nhiều học sinh. Tuy nhiên, nếu có một chiến lược học tập đúng đắn, bạn hoàn toàn có thể đạt được điểm 9-10 môn Toán.

Dưới đây là Top bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10 giúp bạn chuẩn bị tốt nhất cho kỳ thi sắp tới. Hãy cùng Bamboo tìm hiểu và áp dụng những mẹo học này để nâng cao khả năng giải bài tập Toán của bạn!

• Đề thi thử lớp 10 TPHCM mới nhất năm 2025 [có đán án]
• Top các ứng dụng ôn thi toàn lớp 10 đáng dùng nhất

Top 5 bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10

1. Nắm vững các khái niệm cơ bản và công thức quan trọng

Môn Toán không chỉ đơn thuần là việc ghi nhớ công thức mà quan trọng hơn là hiểu rõ từng khái niệm, định lý. Các chủ đề như đại số, hình học, lượng giác và xác suất luôn có những công thức chủ chốt mà nếu nắm vững, bạn có thể giải quyết được phần lớn các bài toán trong đề thi.

Khi bạn hiểu rõ lý thuyết, việc áp dụng công thức vào bài toán sẽ trở nên dễ dàng và hiệu quả hơn. Những khái niệm cơ bản là nền tảng vững chắc cho bạn trong suốt quá trình ôn luyện.

Các công thức cần ghi nhớ

Công thức là công cụ không thể thiếu trong môn Toán. Dưới đây là một số công thức quan trọng bạn cần ghi nhớ:

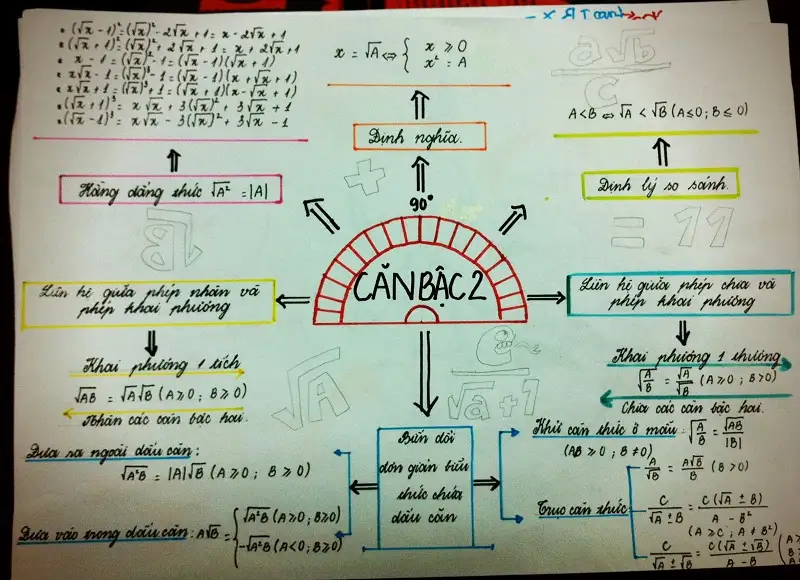
1. Căn bậc hai và hằng đẳng thức đáng nhớ

• Căn bậc hai của a bình phương bằng giá trị tuyệt đối của a:
  √(a²) = |a|

• Bình phương một tổng:
  (a + b)² = a² + 2ab + b²

• Bình phương một hiệu:
  (a – b)² = a² – 2ab + b²

• Hiệu hai bình phương:
  a² – b² = (a – b)(a + b)

• Lập phương một tổng:
  (a + b)³ = a³ + 3a²b + 3ab² + b³

• Lập phương một hiệu:
  (a – b)³ = a³ – 3a²b + 3ab² – b³

2. Phương trình bậc hai

• Công thức nghiệm:
  x = (-b ± √(b² – 4ac)) / 2a

• Công thức nghiệm thu gọn (khi a = 1):
  x = (-b’ ± √(b’² – c)) / a, với b’ = b / 2

• Hệ thức Vi-ét:
  Nếu phương trình có hai nghiệm x₁, x₂ thì:
  x₁ + x₂ = -b / a
  x₁ * x₂ = c / a

Top 5 bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10

3. Hệ phương trình bậc nhất hai ẩn

• Hệ phương trình có dạng:
  a₁x + b₁y = c₁
  a₂x + b₂y = c₂

• Quy tắc nghiệm:

  • Nếu (a₁ / a₂) = (b₁ / b₂) ≠ (c₁ / c₂) thì hệ phương trình vô nghiệm.

  • Nếu (a₁ / a₂) ≠ (b₁ / b₂) thì hệ phương trình có nghiệm duy nhất.

• Phương pháp giải:

  • Phương pháp thế: Biến đổi một phương trình theo một ẩn rồi thay vào phương trình còn lại.

  • Phương pháp cộng đại số: Cộng hoặc trừ hai phương trình để loại bỏ một ẩn.

4. Hình học

• Diện tích tam giác: S = 1/2 * a * h, với a là cạnh đáy, h là chiều cao.

• Định lý Pythagoras (tam giác vuông): a² + b² = c², với c là cạnh huyền.

• Định lý Cosin: c² = a² + b² – 2ab * cosC.

• Định lý Sin: a / sinA = b / sinB = c / sinC = 2R, với R là bán kính đường tròn ngoại tiếp tam giác.

• Bán kính đường tròn nội tiếp tam giác: r = S / p, với p = (a + b + c) / 2 là nửa chu vi tam giác.

5. Hệ thức lượng trong tam giác vuông

• Chiều cao trong tam giác vuông: h² = b’ * c’, với b’, c’ là các đoạn chiếu của hai cạnh góc vuông lên cạnh huyền.

• Định lý Pitago đảo: Nếu a² + b² = c², tam giác là vuông.

6. Giải bài toán bằng cách lập phương trình

• Khi gặp bài toán thực tế, ta có thể lập phương trình dựa trên các công thức sau:

  • Công thức chuyển động: S = v * t, với S là quãng đường, v là vận tốc, t là thời gian.

  • Công thức công việc: W = P * T, với W là khối lượng công việc, P là năng suất, T là thời gian làm việc.

  • Công thức tỉ số phần trăm: Số phần trăm = (Giá trị thực tế / Giá trị tổng) * 100%.

7. Góc nội tiếp và góc tạo bởi tiếp tuyến

• Góc nội tiếp bằng một nửa số đo cung bị chắn: Góc nội tiếp = 1/2 * số đo cung bị chắn

• Góc giữa tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn một cung: Góc giữa tiếp tuyến và dây cung = Góc nội tiếp cùng chắn cung đó.

8. Tỉ số lượng giác của góc nhọn

• sinA = đối / huyền

• cosA = kề / huyền

• tanA = đối / kề

• cotA = kề / đối

2. Tập trung vào các bài tập đặc biệt và các chủ đề quan trọng

Top 5 bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10

Các chủ đề thường gặp trong đề thi lớp 10

Kỳ thi tuyển sinh lớp 10 sẽ có những phần kiến thức chủ yếu được ra trong đề thi, bao gồm:

• Đại số (phương trình, bất phương trình, hệ phương trình).

• Hình học (các định lý hình học, diện tích, thể tích).

• Lượng giác (công thức cơ bản và phương pháp giải bài toán lượng giác).

Việc hiểu rõ các chủ đề này và cách thức giải quyết từng dạng bài sẽ là bí quyết đạt điểm 9 10 môn Toán trong kỳ thi tuyển sinh lớp 10.

Luyện tập các dạng bài tập đặc biệt

• Hệ phương trình: Đây là một dạng bài hay xuất hiện trong đề thi. Bạn cần luyện tập cách giải hệ phương trình một cách linh hoạt và nhanh chóng.

• Đồ thị hàm số: Nắm vững cách vẽ đồ thị và xác định các yếu tố như giao điểm, độ dốc, v.v.

• Bài toán hình học: Đây là phần nhiều học sinh gặp khó khăn. Bạn cần nắm vững các định lý cơ bản và thường xuyên luyện tập với các bài toán về hình học phẳng và không gian.

• Luyện tập đề thi thử: Làm đề thi thử không chỉ giúp bạn làm quen với cấu trúc đề thi mà còn giúp bạn rèn luyện tốc độ làm bài. Sau khi làm xong, bạn cần phải kiểm tra lại các lỗi sai để rút kinh nghiệm và cải thiện kỹ năng.

>>> Xem thêm: Đề thi thử lớp 10 TPHCM mới nhất năm 2025 [có đán án]

3. Đưa ra lộ trình ôn thi hợp lý 

Xây dựng kế hoạch ôn thi chi tiết

Việc ôn thi cần phải có một kế hoạch ôn thi rõ ràng. Bạn không thể chỉ học “lướt qua” các chủ đề mà phải phân bổ thời gian cho từng phần cụ thể. Một lộ trình học tập hợp lý sẽ giúp bạn không bị quá tải và vẫn đảm bảo thời gian ôn luyện cho tất cả các môn, đặc biệt là môn Toán.

• Phân bổ thời gian hợp lý: Dành ít nhất 2-3 tiếng mỗi ngày để ôn môn Toán, và đảm bảo ôn tập cả lý thuyết và bài tập.

• Xây dựng mục tiêu học tập: Mỗi tuần, hãy đặt ra một mục tiêu rõ ràng, chẳng hạn như “hoàn thành bài tập về phương trình bậc 2” hay “luyện 10 đề thi thử về hình học”.

Xem thêm:

Phân bổ thời gian hợp lý cho các bài tập

Khi bạn đã có kế hoạch rõ ràng, việc phân bổ thời gian cho từng phần trong bài thi là rất quan trọng. Đừng dành quá nhiều thời gian cho những bài dễ mà bỏ qua các bài khó.

• Luyện bài tập dễ trước để lấy lại tự tin.

• Dành thời gian nhiều hơn cho các bài khó để làm quen với các dạng bài khó khăn hơn.

4. Phân phân tích đề thi của các năm trước 

Top 5 bí quyết đạt điểm 9 10 môn Toán trong kỳ tuyển sinh lớp 10

Phân tích đề thi cũ giúp bạn hiểu được cách ra đề của các năm trước và làm quen với các dạng câu hỏi thường gặp. Bạn sẽ nhận ra rằng có một số chủ đề luôn xuất hiện và bạn cần đặc biệt chú trọng ôn luyện.

• Những câu hỏi dễ và khó: Xác định rõ những câu hỏi bạn có thể làm nhanh và những câu hỏi cần thời gian giải quyết.

• Cấu trúc đề thi: Hiểu rõ cấu trúc đề thi giúp bạn không bị bất ngờ khi vào phòng thi.

Cách làm đề thi thử hiệu quả

• Làm đúng theo thời gian quy định để rèn luyện tốc độ làm bài.

• Đánh giá kết quả sau mỗi lần làm đề thi thử. Tìm ra những lỗi sai và ôn tập lại những phần yếu.

5. Rèn luyện kỹ năng giải quyết bài tập một cách Logic và kỹ năng

Kỹ năng giải quyết bài toán nhanh và chính xác

Môn Toán yêu cầu bạn có khả năng làm bài nhanh nhưng vẫn phải đảm bảo độ chính xác. Bạn không thể dành quá nhiều thời gian cho một câu hỏi mà bỏ qua các câu khác.

• Phân tích bài toán kỹ lưỡng: Đọc kỹ đề bài và xác định phương pháp giải quyết trước khi bắt tay vào làm.

• Giải quyết bài toán theo từng bước: Đừng vội vàng, hãy giải quyết từng bước một cách logic và rõ ràng.

Trình bày bài thi rõ ràng, mạch lạc

Một phần quan trọng không kém trong kỳ thi là cách bạn trình bày bài thi. Việc trình bày rõ ràng không chỉ giúp giáo viên dễ dàng chấm điểm mà còn giúp bạn không bỏ sót những bước giải quyết quan trọng.

• Viết câu trả lời đầy đủ: Tránh viết tắt hoặc chỉ ghi công thức mà không giải thích.

• Giải thích mỗi bước làm: Điều này giúp bạn ghi điểm ngay cả khi kết quả cuối cùng không chính xác.

Kết luận

Chinh phục điểm 9-10 môn Toán trong kỳ thi lớp 10 không phải là điều quá khó nếu bạn nắm được các bí quyết đạt điểm 9 10 môn toán. Bằng cách nắm vững kiến thức cơ bản, luyện tập các dạng bài đặc biệt, xây dựng kế hoạch ôn thi khoa học, làm đề thi thử và rèn luyện kỹ năng giải quyết bài tập

Hãy bắt đầu ôn luyện từ hôm nay và kiên trì với những bí quyết trên để đạt được kết quả tốt nhất. Bamboo chúc bạn thành công trong kỳ thi tuyển sinh lớp 10 và đạt điểm cao môn Toán!

Đọc thêm:

• Điểm chuẩn lớp 10 năm 2024 chính xác nhất
• Tư vấn chọn trường lớp 10: Định hướng tương lai cho học sinh
• Top các ứng dụng ôn thi toàn lớp 10 đáng dùng nhất